Автоматизация конструкторского и технологического проектирования
Жигалова Е.Ф.
(Кафедра КСУП)
Томск-2005

Компоновка.

№ 1
Что понимается под задачей компоновки ЭВА?
• При иерархической организации конструкции ЭВА под компоновкой понимают определение состава типовых конструкций каждого уровня.
• Под компоновкой понимаются задачи объединения модулей низшего (i-1)-го уровня в модули более высокого i-го уровня по заданному критерию оптимизации и при наличии заданных ограничений.

№ 2
Критерии оптимальности при решении задач компоновки.
• Минимум суммарного числа типов модулей i-го уровня схемы.
• Минимум межблочных соединений.

№ 3
Исходными данными для решения задачи компоновки является коммутационная схема, представленная в виде графа.

№ 4
Разбиением (разрезанием) графа G-(X,U) называется такая совокупность его частей B(G), что:
• ∀(G_i)∈B(G) и G_i≠0, i∈I;
• ∪(G_i)=G;
• ∀G_i, (G_j)∈B(G) (G_i≠G_j→ X_i∩X_j=0 shlap U_i∩U_j=0).

№ 5
Задачей разбиения графа G=(X,U) является нахождение такой совокупности частей, чтобы число реберного соединения графа G удовлетворяло заданному критерию оптимальности.

№ 6
модуль - элементы структурных уровней в конструкциях ЭВА,
шкаф - унифицированные части элементов структурных уровней,
типовой элемент замены - схемные сочетания интегральных микросхем на втором уровне конструктивно-технической базы ЭВА.

№ 7
Исходные данные, необходимые для решения задачи компоновки с минимальной стоимостью ячеек с использованием алгоритма Селютина.
• Заданный конструктивный базис проектирования.
• Информация о логических типах элементов в составе ячеек заданного конструктивного базиса.
• Данные по числу каждого типа элементов, содержащихся в функциональной схеме, которые соответствуют типам элементов ячеек заданного конструктивного базиса.
• Стоимость (вес) ячеек заданного конструктивного базиса.

№ 8
Задача компоновки. Последовательность номеров шагов алгоритма Селютина, в которой они должны выполняться (в рамках одной итерации).
1. Упорядочить ячейки заданного набора по возрастанию их стоимости.
2. Определить вектор M числа непокрытых элементов в схеме по типам.
3. Определить локально-минимальное число ячеек наименьшей стоимости, необходимое для покрытия заданной функциональной схемы.
4. Определить новые значения элементов вектора М. Если М=0, выполнить шаг < определить шаг алгоритма самостоятельно >, иначе шаг <определить шаг алгоритма самостоятельно>.
5. Посчитать число использованных ячеек каждого типа, используемых для покрытия заданной функциональной схемы.

№ 9
Решить задачу компоновки ячеек с несвязными элементами, используя алгоритм Селютина.
Даны:
1) Вектор М, элементы которого равны числу элементов типа t1, t2, t3, t4, используемых в схеме. М=(5,4,1,1);
2) Матрица T состава заданного набора ячеек Я1, Я2, Я3:

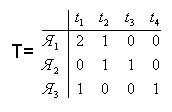
3) Стоимость ячеек: с1<с2<с3<с4.
Определить значения элементов вектора М после выполнения 1-ой итерации.
• (1; 2; 1; 1)

№ 10
- Определить значения элементов вектора М после выполнения 2-ой итерации. Значения элементов перечислить через точку с запятой.
• (1; 1; 0; 1)

Размещение.

Дана математическая модель задачи размещения:
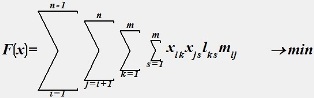(1)
при условиях:
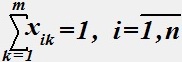(2) 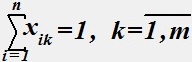(3) x_ik=(1,0) (4).

№ 11
Названия для выражений 1, 2-4 в терминах математического программирования:
(1) - Целевая функция;
(2-4) - Условия ограничения.

№ 12
Если значение индексной переменной i равно номеру размещаемого компонента, а значение индексной переменной k равно номеру позиции, на которую компонент размещается, то x_ik=1:
• если i-й компонент назначается на позицию k.

№ 13
Дать интерпретацию для выражения (2), если значение индексной переменной i равно номеру размещаемого компонента, а значение индексной переменной k равно номеру позиции, на которой компонент размещается.
• Каждый компонент разместится только на одной позиции.

№ 14
- для выражения (3).
• На каждую позицию будет назначено не более одного компонента.

--------------------
при условиях:
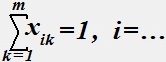(2)
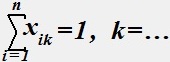(3)
x_ik={1, если компонент d_i назначается на позицию q_k;
,0 в противном случае. (4)

№ 15
Определить область значений переменных i и k , если на монтажной плате возможно разместить 9 ячеек, а требуется разместить 8 ячеек
i=x1-x2; k=x3-x4.
• х1=1; х2=8; х3=1; х4=9

№ 16
- переменной s.
s=x1-x2.
• х1=1; х2=9

Задача размещения. Последовательно-итерационный метод.

Монтажная площадка с координатами s@mul$t.

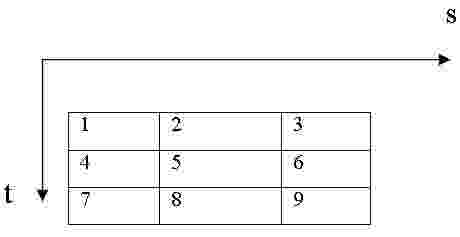
На монтажную площадку наложена граф-сетка так, что номера вершин совпадают с номерами узлов координатной сетки.
Дана матрица смежности R= |r_ij| _9×9 графа G, интерпретирующего схему, с элементами:

№ 17
r_1,4=3, r_1,7=2, r_1,8=3, r_4,6=5, r_5,6=2, r_6,8=6, r_2,3=2, r_2,4=1, r_3,2=2, r_7,9=2, r_5,9=4, r_3,5=2, r_7,8=3.
Вычислить среднюю длину ребра L_j для вершины с номером j=9.
• 2

№ 18
r_1,4=3, r_1,7=4, r_1,8=3, r_4,6=5, r_5,6=2, r_6,8=6, r_2,3=2, r_2,4=1, r_3,2=2, r_7,9=4, r_5,9=4, r_3,5=2, r_7,8=6, r_7,6=10.
- для вершины с номером j=7.
• 2,2

№ 19
r_1,4=3, r_1,7=2, r_1,8=3, r_4,6=10, r_5,6=4, r_6,8=12, r_2,3=2, r_2,4=1, r_3,2=2, r_7,9=2, r_5,9=4, r_3,5=2, r_7,8=3, r_7,6=10.
- координаты центра тяжести s(6); t(6) для вершины с номером 6.
• 1,4; 1,4

№ 20
r_1,4=3, r_1,7=2, r_1,8=3, r_4,6=10, r_5,6=4, r_6,8=12, r_2,3=2, r_2,4=1, r_3,2=2, r_7,9=2, r_5,9=4, r_3,5=2, r_7,8=3, r_7,6=10.
Произведена условная перестановка вершин x₆ и x₅.
- среднюю длину L₆⁵ для вершины x₆, если она помещена в узел с номером 5 (в виде дроби m/n).
• 23/18

Трассировка.

Дана математическая модель (1-3) задачи трассировки.
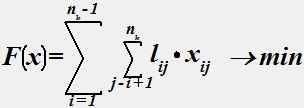(1)
при условиях:
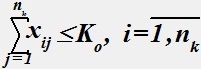(2)
x_ij=(1;0) (3)

№ 21
Дать интерпретацию условия (2):
• максимальное число соединений в одной точке электрической цепи.

№ 22
- условия (3):
• переменная х_ij может принимать значение, равное 1, если ребро (i,j) длиной l включается в связывающую сеть;
• переменная х_ij может принимать значение, равное 0, если ребро (i,j) длиной l не включается в связывающую сеть.

№ 23
Какими условиями следует дополнить математическую модель (1-3), чтобы при решении задачи трассировки гарантировать связность определяемой сети?
•
•

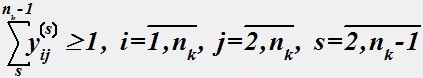
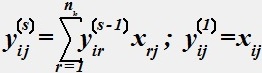
№ 24
Дана математическая модель (1-5) задачи трассировки.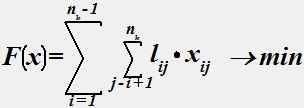
(1)
при условиях: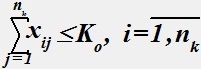
(2)
x_ij=(1;0) (3)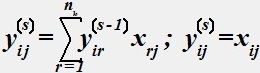
(4)
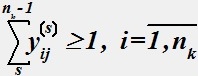(5)
Определить ошибку в записи математической модели (1-5) - построения минимальной связывающей сети.
• В условиях (4,5) необходимо указать область допустимых значений для переменной j: j=2,n_k и для индексной переменной s: s=2,n_k-1.

№ 25
Для проводного монтажа задача трассировки сводится к построению на вершинах графа дерева с минимальной суммарной длиной ребер, при этом вершины графа моделируют соединяемые контакты, а ребра - соединения.

№ 26
Основные критерии трассировки.
• Суммарная длина проводников.
• Максимальная разводимость соединений в пределах возможностей алгоритма и соблюдения заданных ограничений.
• Число пересечений проводников.
• Число монтажных слоёв.
• Число межслойных переходов.

№ 27
Для решения задачи трассировки соединений могут использоваться следующие алгоритмы:
• aлгоритм Ли;
• aлгоритм Прима;
• волновой алгоритм;
• лучевой алгоритм;
• деревья Штейнера;
• канальные алгоритмы.

№ 28
Основная задача трассировки формулируется следующим образом: по заданной схеме соединения проложить необходимые пути прохождения проводников на плоскости, чтобы реализовать заданные электрические соединения с учётом заданных ограничений.

№ 29
Алгоритм Прима основан на соединении пар точек в соответствии с правилами:
• если следующая пара наиболее близко расположенных вершин представляет собой два контакта, для которых трасса соединений уже существует, то эта пара пропускается;
• две вершины (два контакта) соединяются кратчайшим путем, если они ближе всего расположены друг к другу;
• из множества неподсоединенных вершин выбирается та, которая находится ближе остальных к ранее связанным вершинам и присоединяется к ним кратчайшим путем.

№ 30
Граф G=(X,U) схемы задан матрицей смежности

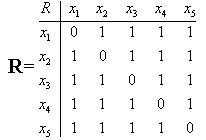
• Граф G -не планарный.

САПР.

№ 31
На чем основано выполнение проектных операций и процедур в САПР?
• На оперировании математических моделей.

№ 32
Определение понятию “синтез” технического объекта в САПР.
Задача синтеза технического объекта состоит в том, чтобы по заданному функциональному назначению объекта или закону функционирования получить проектное решение в виде описания проектируемого объекта.

№ 33
При синтезе электронных схем в САПР должны быть заранее заданы:
• допустимый набор используемых элементов;
• возможные правила соединения элементов между собой;
• способы определения по синтезированной структуре объекта функции, которую он реализует.

№ 34
Под конструкцией ЭВА понимают:
• совокупность электрически и механически соединенных элементов, в которой реализуется электрическая схема данной ЭВА.

№ 35
При проектировании технического объекта под оптимальным вариантом структур и конструкций понимают:
• такой вариант конструкции или структуры, параметры которой удовлетворяют всем системным, конструктивным, технологическим, электрическим, экономическим требованиям ТЗ; для которого критерий оптимальности, описывающий качество проектируемой структуры или конструкции, принимает минимальное или максимальное значение.

№ 36
Проектирование топологии электронных схем - это:
• процесс преобразования электрической или логической схемы в описание реализации схемных компонентов и связей между ними.

№ 37
Основные уровни конструкции вычислительной аппаратуры следующие:
• элементы-конструктивы,
• типовые элементы замены (ячейки),
• блоки,
• шкафы.

№ 38
Типовые элементы замены (ячейки) - это унифицированные для одного изделия конструктивные элементы, объединенные на одной печатной плате.

№ 39
Конструктивно-технологические особенности печатных плат (ПП):
• ПП представляет собой составную пластину, на поверхностях которой размещены элементы;
• ПП могут быть двухслойными;
• электрическая связь между выводами элементов, размещенных на ПП, обеспечивается печатными проводниками, нанесенными на поверхности.

№ 40
Укажите программы САПР PCAD 4.5, предназначенные для редактирования схемы электрической принципиальной, корректировки схемных библиотечных элементов, подготовки конструктива печатной платы, создания конструкторско-технологической библиотеки, автоматической трассировки печатной платы.
• PC-CAPS;
• PC-CARDS;
• PC-ROUTE.

Математические модели объектов проектирования.

№ 41
Под математической моделью объекта проектирования понимают множество ограничений, условий, описывающих функционирование объекта и реализующих заданные математические методы для определения требуемых характеристик объекта.

№ 42
Выходные параметры системы - это:
• величины, характеризующие свойства системы.

№ 43
Внешние параметры системы - это:
• величины, характеризующие свойства внешней среды.

№ 44
Внутренние параметры системы - это:
• величины, характеризующие свойства элементов системы.

№ 45
К внутренним параметрам блоков ЭВА относятся:
• параметры транзисторов;
• тепловые характеристики элементов;
• емкости конденсаторов.

№ 46
К внешним параметрам блоков ЭВА относятся:
• давление;
• напряжение источников питания;
• радиационное излучение;
• температура окружающей среды;
• влажность.

№ 47
К выходным параметрам блоков ЭВА относятся:
• число каналов;
• быстродействие;
• частота;
• объем внутренней памяти.

№ 48
Какие математические модели наиболее часто используются при решении основных конструкторских задач покрытия, типизации, компоновки, размещения и трассировки?
• Структурные.
• Дискретные модели.

№ 49
Для построения математической модели (ММ) коммутационной схемы (КС) при решении задач компоновки и размещения следует выполнить:
• задать КС в виде неориентированного графа G=(X',X'',U);
• компоненты (элементы) КС представляются вершинами X';
• внешние контакты представляются вершинами X'';
• каждая электрическая цепь e_i∈E представляется в графе G полным подграфом, включающим все вершины, инцидентные цепи e_i;
• вес ребра u_ij∈U определяется числом связей между элементами КС.

№ 50
- при решении задач трассировки и планарности:
• задать КС в виде неориентированного графа G=(X',X'',U);
• компоненты (элементы) КС представляются вершинами X';
• внешние контакты представляются вершинами X'';
• каждая электрическая цепь e_i∈E представляется в графе G покрывающим деревом.

Решение задач.

Пусть граф схемы G=(X,U), гдеX"=9 задан матрицей смежности R, элементы которой равны:
r₁₄=3, r₁₇=2, r₁₈=3, r₂₃=2,
r₂₄=1, r₃₅=2, r₄₆=5, r₅₆=2,
r₅₉=4, r₆₇=5, r₆₈=6, r₇₈=3,
r₇₉=2, остальные элементы r_ij равны нулю.
Граф G отображен в сетку G_r, нанесенную на монтажную плоскость с числом посадочных мест D=3×3. На монтажную плоскость нанесена система координат s×t с начальными координатами 1×1 в левом нижнем углу данной плоскости.
Вершинам х_i∈X сопоставлены посадочные места d_ts на монтажной плоскости следующим образом:
x₁→d₁₃, x₂→d₂₃, x₃→d₃₃, x₄→d₁₂, x₅→d₂₂, x₆→d₃₂, x₇→d₁₁, x₈→d₂₁, x₉→d₃₁.

№ 51
Вычислить среднюю длину ребер, инцидентных вершине х₆ после её перестановки на место вершины х₄.
• 29/18

№ 52
- инцидентных вершине х₆ после её перестановки на место вершины х₅.
• 23/18

№ 53
- инцидентных вершине х₆ после её перестановки на место вершины х₇.
• 30/18

№ 54
- инцидентных вершине х₄ после её перестановки на место вершины х₆.
• 21/9

№ 55
- инцидентных вершине х₆ после её перестановки на место вершины х₈.
• 29/18

№ 56
- инцидентных вершине х₅ после её перестановки на место вершины х₆.
• 5/5

№ 57
Вычислить величину отклонения σ₆⁵ вершины х₆ после её перестановки на место вершины х₅, если среднюю длину ребер, инцидентных вершине х₆ после её перестановки на место вершины х₅ равна ≈1,3.
• 0,9

№ 58
- σ₆⁵ вершины х₆ после её перестановки на место вершины х₅, если среднюю длину ребер, инцидентных вершине х₆ после её перестановки на место вершины х₅ равна ≈2,2.
• 0,9

№ 59
- σ₆⁴ вершины х₆ после её перестановки на место вершины х₄, если среднюю длину ребер, инцидентных вершине х₆ после её перестановки на место вершины х₄ равна ≈2,2.
• 0,6

№ 60
- σ₆⁷ вершины х₆ после её перестановки на место вершины х₇, если среднюю длину ребер, инцидентных вершине х₆ после её перестановки на место вершины х₇ равна ≈1,7.
• 0,5

Методология автоматизированного проектирования.

Для схемы

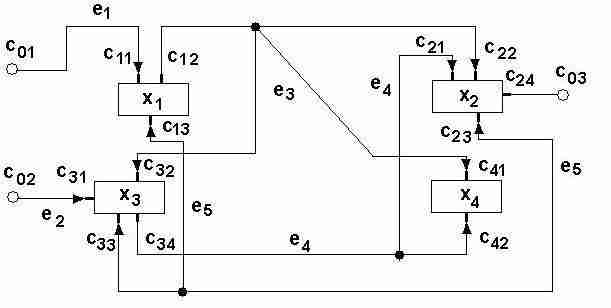
построить математическую модель коммутационной схемы (КС) в виде неориентированного графа G=(X,U).
Принять следующее соответствие элементов и внешних контактов данной КС вершинам X графа G:
x→x₁, x₂→x₂, x₃→x₃, x₄→x₄, C₀₁→x₅, C₀₂→x₆, C₀₃→x₇.

№ 61
Каждая электрическая цепь e_i представлена полным подграфом, включающим все вершины, инцидентные цепи e_i.
Значения элементов треугольной матрицы смежности R графа G по строкам (начиная с первой строки):
• (0, 2, 2, 1, 1, 0, 0, 0, 3, 2, 0, 0, 1, 0, 2, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)

№ 62
Полные подграфы, моделирующие электрические цепи e_i, представлены покрывающими их деревьями. Корнями деревьев являются следующие вершины графа G:
х₁ - для цепей e₅, e₃; х₂ - для цепи e₄.
• (0, 2, 2, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)

№ 63
Полные подграфы, моделирующие электрические цепи e_i, представлены покрывающими их деревьями. Все покрывающие деревья графа G являются звездными подграфами со следующими центральными вершинами: x₁ для цепей e₅, e₃; х₃ - для цепи e₄.
• (0, 2, 2, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)

№ 64
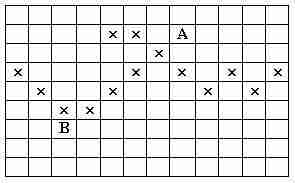
Дискретное рабочее поле (ДРП):

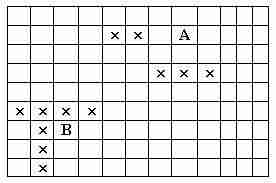
Точка А - источник. Точка В - цель. Запрещенные ячейки ДРП помечены 'x'.
Используя волновой алгоритм, определить минимальное значение номера фронта Фк волны, достигающей цель В. Принять начальное значение номера фронта к=1.
Для проводника не допустимы диагональные направления.
• 9

№ 65

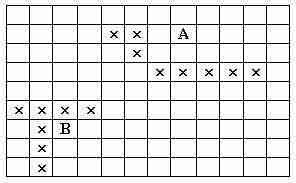
• 13

№ 66

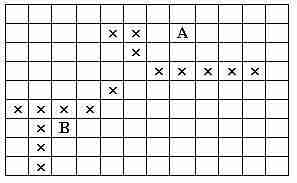
• 15

№ 67

• Ø

№ 68
Пусть А₁,А₂ - размеры коммутационного поля. А₁=12, А₂=10. h - дискрет ДРП. Проводники имеют следующую ширину h₁={0.2,0.5,0.1,0.3}. Допустимые расстояния между проводниками h₂={0.6,0.4,0.7}.
Определить число дискретов h по осям ОХ, OY.
• 24, 20

№ 69
А₁=12, А₂=12. h₁={0.2,0.5,0.1,0.3}. h₂={0.6,0.5,0.8}.
• 20, 20

№ 70
А₁=22, А₂=32. h₁={2,5,1,3}. h₂={0.6,0.5,0.8}.
• 15, 21

Автоматизация технологического проектирования.

№ 71
Технологическая подготовка производства электронно-вычислительной аппаратуры связана:
• с разработкой наиболее экономичного для данных производственных условий варианта перехода от описания конструкции в виде математической модели к готовому изделию;
• с решением задачи обеспечения технологичности конструкции изделия;
• с проектированием оптимальных технологических процессов изготовления специальной технологической оснастки (фотошаблонов БИС, печатных плат, приспособлений для сверления отверстий в печатных платах и т.п.);
• с разработкой технологической документации операционных технологических карт.

№ 72
Проектирование технологических процессов производства радио-электронной и электронно-вычислительной аппаратуры включает в себя:
• разработку принципиальной схемы технологического процесса;
• проектирование технологического маршрута обработки изделия;
• проектирование технологического маршрута технологических операций и переходов;
• получение управляющих программ для станков с ЧПУ.

№ 73
Исходные данные для проектирования технологического процесса.
• Конструкторская документация в виде рабочих чертежей изделия.
• Допустимые варианты технологической оснастки.
• Нормативная и справочная документация.
• Плановые задания на объем выпуска изделия.

№ 74
Основные направления перспективного развития математических методов решения прикладных задач конструирования радиоэлектронных средств.
• Решение задач векторной оптимизации.
• Разработка адекватных исследуемому объекту математических моделей и имитационное моделирование с помощью цифровых и аналоговых ЭВМ.
• Разработка решающих правил в теории распознавания образов для формирования целевых функций при конструировании РЭС.
• Развитие систем автоматизированного проектирования в направлении охвата конструкторских задач.

№ 75
На каких принципах строится элементная база радиоэлектронных систем?
• Интегральный принцип.

№ 76
Требования, предъявляемые к покрытию функциональной или электрической принципиальной схемы РЭС:
• точность;
• быстродействие;
• экономичность;
• надежность.

№ 77
Отношение, определяющее показатель эффективности Э_ij РЭС по критерию надежности, если C_i - стоимость модулей, P_ij - вероятность безотказной работы совокупности модулей, необходимых для реализации изделий по i - стратегии, t_i - время выполнения типовой вычислительной операции элементной базой, выбранной по i-ой стратегии, N_i - общее число внешних выводов конструктивных модулей, применяемых в изделии по i-ой стратегии, W_i - энергия, потребляемая всеми модулями изделия при выборе элементной базы i-ой стратегии.
• Э_ij=P_ijC_i.

№ 78
- по быстродействию.
• Э_ij=1/C_it_i.

№ 79
-по критерию минимального энергосбережения.
• Э_ij=1/W_iC_i.

№ 80
Методы, применяемые для решения конструкторско-технологических задач.
• Методы статистических игр.
• Формальные методы.
• Метод статистических испытаний.
• Методы теории массового обслуживания.

Автоматизация функционально-логического проектирования.

№ 81
Основные задачи функционально-логического проектирования цифровой аппаратуры.
• Разработка алгоритмов, реализующих воплощаемые в аппаратуре функции.
• Синтез и верификация функциональных и принципиальных схем.
• Разработка контролирующих и диагностирующих тестов.

№ 82
Результат процедуры синтеза при проектировании функциональных схем электронно-вычислительной аппаратуры:
• Функциональная или принципиальная схемы устройств, построенные в заданном элементном базисе.

№ 83
Классический метод синтеза комбинационных схем, основанный на минимизации булевых функций.
• Метод Квайна - Мак - Класки.

№ 84
• Техническое диагностирование - это определение технического состояния устройства с целью установления факта неисправности и отбраковки неисправных объектов и установления места неисправного объекта.

№ 85
Классификация неисправностей (дефектов) электронных устройств.
• Устойчивые и неустойчивые.
• Одиночные и кратные.
• Константные - проявляются как постоянные уровни сигналов в соответствующей цепи и называемые константными нулем (=0) и единицей (=1).
• Правильные (не изменяющие тип цифрового устройства) и неправильные (изменяющие тип цифрового устройства).

№ 86
Что представляют собой элементарные составляющие в модели дискретных устройств?
• Модели корпусов микросхем.

№ 87
Исходные данные для синтеза функциональных и логических схем.
• Техническое задание, которое содержит результаты предыдущих этапов проектирования.
• Описание структурных схем с указанием требований к выходным параметрам: быстродействие, точность обработки информации, надежность и т.п.
• Результаты предыдущих этапов, которые представляются в виде описания алгоритмов функционирования.

№ 88
Определение микропрограммного автомата (МПА) с жесткой логикой.
• МПА - это конечный автомат, имеющий память, состояние которой отождествляется с состоянием конечного автомата; имеющий комбинационную часть, вырабатывающую сигналы для управления операционными блоками и для изменения собственного состояния.

№ 89
Процедура минимизации числа внутренних состояний микропрограммного автомата (МПА) основана на поиске эквивалентных состояний МПА и их отождествлении.

№ 90
Выполнение процедуры минимизации числа внутренних состояний микропрограммного автомата ведет к сокращению аппаратных затрат и повышению его надежности.

Схемотехническое проектирование, анализ и верификация конструкторского проектирования.

№ 91
Схемотехническое проектирование - это процесс разработки технической документации принципиальных электрических схем в соответствии с требованиями технического задания.

№ 92
Основные типы проектируемых схем:
• аналоговые;
• цифровые;
• цифроаналоговые.

№ 93
Автоматизация схемотехнического проектирования предполагает решение на ЭВМ задач:
• выбора конфигурации электронной схемы (структурный синтез);
• предварительный расчет параметров элементов схемы, предварительный расчет параметров элементов схемы на основе упрощенных формул и соотношений;
• определение выходных параметров схемы в зависимости от изменения внутренних и внешних параметров;
• определение выходных параметров схемы одновариантного и многовариантного анализа;
• параметрической оптимизации.

№ 94
Автоматизированное решение задач анализа и оптимизации основано на инвариантных методах и алгоритмах.

№ 95
Полной моделью схемы называется:
• математическая модель схемы, полученная непосредственным объединением моделей компонентов в общую систему уравнений, на основе топологических уравнений.

№ 96
Макромодель схемы - это:
• математическая модель схемы, являющаяся более простой по затратам времени и памяти ЭВМ на ее реализацию, чем полная модель.

№ 97
Для разработки алгоритмов анализа больших, сложных цифровых и цифроаналоговых схем применяются следующие методы:
• разбиения, декомпозиции, основанные на разделении сложной схемы на простые подсхемы с учетом связей между ними;
• методы подсхем, характеризующиеся тем, что на этапе формирования математических моделей систем сначала группируются уравнения отдельных подсхем, а в конце - все граничные уравнения.

№ 98
Инвариантная форма математической модели элемента электронной схемы представляет собой:
• запись системы обыкновенных дифференциальных уравнений безотносительно к методу ее численного решения.

№ 99
Специфика математического обеспечения схемотехнического проектирования проявляется:
• в моделировании элементов электронных схем;
• в анализе конкретных типов проектируемых схем.

№ 100
Базовые эквивалентные схемы состоят из следующих двухполюсников:
• емкости;
• индуктивности;
• резистора;
• источника тока;
• источника напряжения.