Специальные главы математики. Часть 1.
Дискретная математика. Часть 1.
для специальности 220200
Синчинова Л.И.
Кафедра АОИ
Томск-2005

Множества и операции над ними.

№ 1
Для понятия “элемент а не принадлежит множеству А” используется обозначение:
• a∉A.

№ 2
Пусть универсальное множество U=R. Найти множество М решений уравнения x²-9=0.
• {-3.3}

№ 3
Даны множества A={1,2,3,4,5} и B={-5,-4,0,1,2,3,4,5}. Какое из утверждений справедливо?
• A⊂B.

№ 4
На каком рисунке изображено пересечение множеств А и В?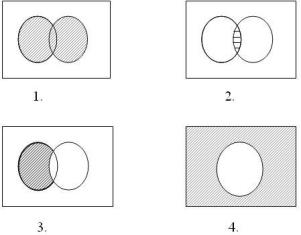

• 2

№ 5
Пусть множество A={5,7,18,19,20}, а множество B={7,19,30}. Найти разность A\\B .
• {5,18,20}

№ 6
Пусть множество A={5,7,18,19,20}, а множество B={7,19,30}. Найти пересечение этих множеств.
• {7,19}

№ 7
Множество всех подмножеств данного множества называется:
• булеаном.

№ 8
Система непустых непересекающихся подмножеств данного множества, в объединении дающих все множество называется:
• разбиением.

№ 9
Система непустых подмножеств данного множества, в объединении дающих все множество называется:
• покрытием.

№ 10
Пользуясь законами алгебры множеств упростить выражение: A∩(A∪B)∪(B∪C)∪B
• B∪C.

№ 11
Вариант, который не задает множество.
• A={а, ф, о, а, е, л, к, о}.

№ 12
Для каких множеств А и В верно утверждение: А не включается в В?
• A={9,7,5,3,11}, B={1,3,5,9,11}.

№ 13
Задано множество X={1,2,3,4,5,6,7,8}. Какая из систем множеств не является его разбиением?
• {1, 3, 6}, {4, 2, 8}, {3, 5, 7}.

№ 14
В магазине десять покупателей купили молоко, 11 — хлеб, 8 — колбасу. Молоко и колбасу купили 4 человека, молоко и хлеб — 6, хлеб и колбасу — 3. Все три продукта купили двое. Сколько покупателей сделали покупки в магазине?
• 18.

№ 15
Двойное дополнение к множеству А, согласно закону алгебры множеств — это:
• множество А.

№ 16
В задаче рассматриваются множества: A={0,5,2,7}, B={3,6,7} и C={4,0}. Какое из множеств является универсальным множеством U элементов, рассматриваемых в данной задаче?
• {0, 3, 4, 5, 2, 6, 7}.

№ 17
Заданы множества A={3,8,10,4,5} и B={2,3,7,4,12}. Какое из множеств является объединением множеств А и В?
• {3, 8, 2, 7, 4, 10, 12, 5}.

№ 18
Какое из множеств является разностью множеств {1,2,3,4,5,6,7,8} и {2,4,6.8}?
• {1,3,5,7}.

№ 19
Дополнением множества А до универсального называется разность универсального множества и множества А.

Бинарные отношения.

№ 20
Пусть A={-1,3},B={0,1,2}. Какое из множеств является декартовым произведением множеств А и В?
• {(-1,0),(-1,1),(-1,2),(3,0),(3,1),(3,2)}.

№ 21
Какое из заданных соответствий является биекцией?

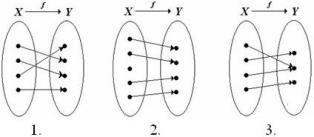
• 1

№ 22
Областью определения бинарного отношения R является:
• {x | (x,y)∈R}.

№ 23
Областью значений бинарного отношения R является:
• {y | (x,y)∈R}.

№ 24
Отношение R на множестве X, для которого ∀x∈X выполняется условие (x, x)∈R называется:
• рефлексивным.

№ 25
Отношение R на множестве X, для которого из условия (x, y)∈R следует (y, x)∈R называется:
• симметричным.

№ 26
Пусть на множестве X={1,2,3,4,5,6} задано отношение S={(x,y) | (x+y) делится на 2}. Записать класс эквивалентности, порожденный элементом 3.
Множество в ответ вводите в фигурных скобках в возрастающем порядке. • {1,3,5}

№ 27
Пусть R – отношение эквивалентности на множестве X и X|R - совокупность всех различных классов эквивалентности по отношению R. Тогда X|R является:
• разбиением X.

№ 28
Пусть X={4,5,9,16,17,19} и на нем задано отношение порядка – x делится на y с остатком 1. Найти максимальный элемент и наименьший элемент.
• Максимальный – 19, наименьшего – нет.

№ 29
Пусть X={1,2,4,8}, Y={1,3,6,12}. R – отношение делимости. Изоморфны ли (X,R) и (Y,R)?
• Изоморфны.

№ 30
Какое из отношений, заданных на множестве X={1,2,3,4,5,6,7} не является рефлексивным?
• {(x,y) | x,y∈X,x+y<10}.

№ 31
Какое из отношений, заданных на множестве X={1,2,3,4,5,6,7} является антирефлексивным?
• {(x,y) | x,y∈X,x>y}.

№ 32
Какое из отношений, заданных на множестве X={1,2,3,4,5,6,7} является симметричным?
• {(x,y) | x,y∈X,x+y<10}.

№ 33
Какое из отношений, заданных на множестве X={1,2,3,4,5,6,7} является антисимметричным?
• {(x,y) | x,y∈X,x≥y}.

№ 34
Какое из отношений, заданных на множестве X={1,2,3,4,5,6,7} не является транзитивным?
• {(x,y) | x,y∈X,x+y<10}.

№ 35
Отношение, обладающее свойствами рефлексивности, антисимметричности, транзитивности, называется отношением:
• порядка.

№ 36
На множестве X = {5, 7, 9, 2, 1} задано отношение R={(x,y) | x,y∈X,x*y-2>5}. Укажите свойство, которым обладает данное отношение.
• Симметричность.

№ 37
На множестве X = {5, 7, 9, 2, 1} задано отношение R={(x,y) | x,y∈X,x*y-2>10}. Укажите свойство, которым обладает данное отношение.
• Симметричность.

№ 38
Задано бинарное отношение P={(1,2),(2,3),(3,4)}. Какое из множеств является его областью значения?
• {2, 3, 4}.

№ 39
Задано бинарное отношение P={(1,3),(2,4),(3,6)}. Какое из множеств является его областью определения?
• {1, 2, 3}.

Реляционная алгебра.

№ 40
Множество R∩S записей, каждая из которых принадлежит как R, так и S называется:
• пересечением.

№ 41
Пусть заданы отношения:

Какое из множеств записей является разностью R\\S ?

• 1

№ 42
Пусть: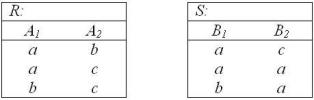

Является ли объединением R∪S множество записей?

• Не является.

№ 43
Задано отношение R:

Какое из отношений является проекцией π_(1,3)R?

• 3

№ 44
Операция селекции отношения R по условию F позволяет получить:
• горизонтальное подмножество.

№ 45
Выполняя вначале операцию декартова произведения отношений R и S, а затем селекцию полученного отношения получаем:
• соединение отношений R и S.

№ 46
Можно ли построить пересечение отношений: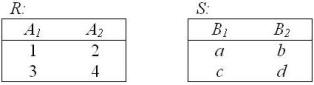

• Нельзя.

№ 47
Операция соединения отношений обозначается:

• 3

№ 48
Являются ли совместимыми отношения: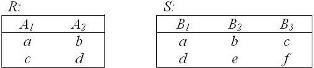

• Не являются.

№ 49
Отношение R задано таблицей, имеющей 6 строк и 4 столбца. Степень отношения R равна:
• 4.

№ 50
Конкатенация записей “квадрат” и “квартал” будет иметь вид:
• “квадратквартал”.

№ 51
Отношение R имеет степень 3, а отношение S — степень 5. Декартово произведение отношений R и S будет иметь степень:
• 8.

№ 52
Чтобы получить соединение отношений R и S по условию F, нужно выполнить следующие действия:
• построить расширенное декартово произведение отношений R и S, а затем выполнить его селекцию по условию F.

Конечные и бесконечные множества.

№ 53
Множества X и Y называются равномощными, если:
• существует биекция X на Y.

№ 54
Пусть X={1,2,3,4,5,6,7,8,9}. Какие из пар множеств равномощны?
• {2} и {x | x∈X, x>8}.

№ 55
Какое из множеств бесконечно?
• множество всех треугольников на плоскости.

№ 56
Пусть множество X конечно и |X|=n. Тогда мощность булеана X равна:
• 2ⁿ.

№ 57
Пусть X является объединением r непересекающихся конечных множеств X_i, i=1,2,...r. Тогда:
• .

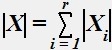№ 58
Множество X счетно, если оно равномощно:
• множеству N натуральных чисел.

№ 59
Какое из множеств является счетным?
• {x | x∈N, x делится на 3}.

№ 60
Является ли счетным множество точек отрезка [0,1]?
• Не,является.

№ 61
Множество X – множество натуральных чисел. Множество Y={x | x∈N, x>20}. Тогда множество X∪Y является:
• счетным.

№ 62
Множество X={1,2,3,4,5,6}. Множество Y={x | x∈N, x – четное}. Какова мощность множества X∩Y ?
• 3.

№ 63
Мощность декартова произведения конечных множеств равна:
• произведению мощностей этих множеств.

№ 64
Если множество X={3,7,2,0}, а множество Y={5,9,0,3}, то мощность X∪Y равна:
• 6.

№ 65
Какому множеству равномощно множество точек отрезка [0, 1]?
• Множеству вещественных чисел.

№ 66
Вставьте пропущенное слово: “Мощность булеана множества X … мощности множества X”.
• Больше.

Комбинаторика.

№ 67
В магазине продается шесть кожаных сумок и восемь клеенчатых. Сколькими способами можно выбрать себе сумку?
• 14

№ 68
В столовой имеется три вида супа и четыре – второго блюда. Сколько способов выбрать себе обед из двух блюд?
• 12

№ 69
На полке стоят книги. Восемь из них – фантастика, девять – приключения. В шести – и приключения, и фантастика. Сколько книг на полке?
• 11

№ 70
Сколько пятизначных телефонных номеров можно составить, если использовать все числа от 0 до 9?
• 100000

№ 71
20 человек решили пойти в кино. В кассе было только 4 свободных билета. Сколькими способами можно выбрать четырех счастливчиков и посадить их на места (номера мест фиксированы)?
• 116280

№ 72
Сколькими способами можно разложить в ряд 10 карандашей разного цвета?
• 3628800

№ 73
Имеется набор цифр: 1,2,3,1,2. Сколько различных пятизначных чисел можно из них получить?
• 30

№ 74
На три вакансии продавца в магазин претендуют 9 человек. Сколькими способами можно укомплектовать штат продавцов?
• 84

№ 75
Сколькими способами 50 студентов можно рассадить в три аудитории, если способы различаются только количеством человек в каждой аудитории?
• 1326

№ 76
Найти количество множеств из 6 элементов, которые можно составить из множества, содержащего 12 элементов.
• 924

№ 77
Найти значение C₂₀¹⁶ / C₁₆².
• 40.375

№ 78
Найти значение C₂₀¹⁶ * C₁₆².
• 581400

№ 79
Сколькими способами можно составить четырехцветный полосатый флаг (все полосы вертикальные), если имеется ткань восьми различных цветов?
• 1680

№ 80
В магазине 10 покупателей купили молоко, 12 — хлеб. И хлеб, и молоко купили 6 покупателей. Сколько человек сделало покупки?
• 16

№ 81
Имеется 6 шоколадных конфет и 15 карамелек. Сколькими способами можно выбрать конфету?
• 21

№ 82
Имеется класс из 10 компьютеров. Сколькими способами можно рассадить в этом классе 8 студентов?
• 1814400

№ 83
Сколько различных наборов из 5 фотографий можно напечатать с 10 негативов (фотографии в наборе могут быть одинаковыми)?
• 2002

№ 84
Сколькими способами можно рассадить 50 студентов по четырем аудиториям?
• 23426

№ 85
Сколькими способами можно выбрать председателя, заместителя и секретаря организации, состоящей из 30 человек?
• 24360

№ 86
Из 25 студентов 10 человек посещают спецкурс по информатике, несколько человек по математике. И по информатике, и по математике посещают спецкурс 6 человек. Сколько студентов посещают спецкурс по математике?
• 21

Бином Ньютона.

№ 87
Общий член бинома Ньютона имеет вид:
• C_n^ka^kb^n-k).

№ 88
Известно, что в формуле бинома Ньютона C₁₀³=18. Чему равен C₁₀⁷?
• 18

№ 89
Известно, что в формуле бинома Ньютона C₁₈⁴=20. Тогда C₁₇⁴ и C₁₇³ могут быть равны:
• 8 и 12.

№ 90
Сумма биномиальных коэффициентов равна:
• 2ⁿ.

№ 91
Известно, что в формуле бинома Ньютона C₄⁰=2, C₄¹=-5, C₄²=2, C₄³=4. Чему равен C₄⁴ ?
• 13

№ 92
Найти член разложения бинома (x+1/x³)ⁿ, не содержащий x, если сумма коэффициентов с четными номерами равна 128.
• 28

№ 93
Найти максимальный коэффициент бинома Ньютона, если n=8.
• 70

№ 94
Вычислить (1,0025)⁵ с точностью до 0,0001.
• 1.0125

№ 95
Биномиальным коэффициентом является величина:
• n! / |r!(n-r)!|.

№ 96
Сколько максимальных коэффициентов имеет бином Ньютона, если n=11 ?
• 2

Группы подстановок.

№ 97
Является ли группой множество натуральных чисел с заданной на нем операцией сложения?
• Не является.

№ 98
Предложенная таблица является подстановкой.
•

1	2	3	4	5
3	2	1	5	4

№ 99
Является ли группой множество всех подстановок с заданной на нем операцией композиции?
• Является.

№ 100
Найти в подстановке стационарный элемент.

1	2	3	4
2	3	1	4

• 4

№ 101
Группы G₁ и G₂ называются изоморфными, если:
• существует биекция f:G₁ → G₂ сохраняющая групповую операцию.

№ 102
Какой порядок имеет группа самосовмещений правильного пятиугольника на плоскости?
• 10

№ 103
Является ли полным циклом подстановка?

1	2	3	4	5
3	4	5	1	2

• Является.

№ 104
Каков порядок подстановки?

1	2	3	4	5
3	4	1	2	5

• 4

№ 105
Какое из множеств с заданной на нем бинарной операцией является группой?
• (R, X).
• (N, X).