
Дискретная математика-1.
для специальностей 230105, 080801
Сафьянова Е.Н.
Кафедра АСУ
Томск-2006
№ 1
Описательный способ задания множества состоит:
• в том, что указывается характерное свойство, которым обладают все элементы множества.
№ 2
Как записать математически следующее множество: «Множество X состоит из элементов x множества M таких, что x является менеджером фирмы»?
• X = {x ∈ M/x - менеджер фирмы}.
№ 3
Что означает следующая запись: X ⊂ Y?
• Множество X является подмножеством множества Y.
№ 4
Какое подмножество может быть сформулировано в виде: ∀x [x∈X => x∈Y]?
• Для любого элемента x утверждение «x принадлежит X» влечет за собой утверждение «x принадлежит Y».
№ 5
Какое множество отмечено на рисунке затемнением?
• Пересечение множеств Х и Y.
№ 6
Что означает выражение: ![]()
• Объединение множеств Xi (i = 1, 2, ... N).
№ 7
Каков правильный вывод из следующего выражения: X \\ Y= ∅ ?
• Множество Х является подмножеством множества Y.
№ 8
Какое множество называется дополнительным к множеству M по отношению к множеству N, если M⊂N ?
• Множество, состоящее из элементов N, не принадлежащих множеству M.
№ 9
Даны множества X = {1, 2, 3, 4, 5}, Y = {2, 4, 6, 7}, найдите Y \\ X.
• Y \\ X = {6, 7}.
№ 10
Верно ли, что:
а) {1, 2} ⊆ {{1, 2, 3}, {1, 3}, 1, 2}
б) {1, 2} ∈ {{1, 2, 3}, {1, 3}, 1, 2}?
• Утверждение а) верно, утверждение б) неверно..
№ 11
Пусть I={x1, x2, x3} - универсальное множество, а X={x1, x2}, Y={x2, x3} его подмножества. Определите перечислением декартовы произведения множеств: X×Y, Y×X.
• X×Y = {(x1, x2), (x1, x3), (x2, x2), (x2, x3) }; Y×X={(x2, x1), (x2, x2), (x3, x1), (x3, x2)}.
№ 12
На множестве X={x / x∈N, x<10} задано отношение R: “x и y имеют один и тот же остаток при делении на 2” (x∈X, y∈X). Определите, на какие классы эквивалентности разбивается множество данным отношением.
• {2, 4, 6, 8}; {1, 3, 5, 7, 9}.
№ 13
Отношение R между элементами множества X называется транзитивным, если:
• ∀ x,y,z ∈ X справедливо утверждение: x R y, y R z => x R z.
№ 14
Отношение R между элементами множества X называется симметричным, если:
• ∀ x,y ∈ X справедливо утверждение: x R y => y R x.
№ 15
Отношение R между элементами множества X называется тождественным, если:
• ∀ x,y ∈ X справедливо утверждение: x R y и y R x => x = y.
№ 16
Может ли антисимметрическое отношение одновременно являться тождественным?
• Не может.
№ 17
Может ли антирефлексивное отношение одновременно являться антисимметричным?
• Может.
№ 18
Какими свойствами обладает следующее отношение: “число x не меньше числа y” - на множестве натуральных чисел?
• Рефлексивность, тождественность, транзитивность, полнота.
№ 19
Отношение называется отношением квазипорядка, если оно обладает свойствами:
• рефлексивности и транзитивности.
№ 20
Отношение называется отношением порядка, если оно обладает свойствами:
• рефлексивности, тождественности и транзитивности.
№ 21
Отношение называется отношением эквивалентности, если оно обладает свойствами:
• рефлексивности, симметричности и транзитивности.
№ 22
Какие из отношений являются отношениями строгого порядка?
• “Oтрезок x длиннее отрезка y”.
• “x старше по возрасту, чем y”.
№ 23
Какие из отношений являются отношениями эквивалентности?
• “х и y - оба учатся в ТУСУРе”.
№ 24
Пусть имеется подмножество X′⊂ X, где X - множество, для элементов которого определено отношение порядка. Как называется элемент x∈X, предшествующий всем элементам множества X′, если он может и не принадлежать множеству X′?
• Минорантой множества X′.
№ 25
Решите систему уравнений:
| { | A∩X=B, |
| A∪X=C, |
• X = B U C \\ A.
№ 26
Какой из способов задания графов является верным?
а) Граф G задается множеством точек (вершин) X={x1,..xn} и соответствия G(х), которое показывает, как между собой связаны вершины.
б) Граф G задается множеством точек (вершин) X={x1,..xn} и множеством линий (ребер) A={a1,..,a m}, соединяющих между собой все или часть этих точек.
• Оба способа верны.
№ 27
Что означает запись g(xi, xj) при описании графа?
• Запись g(xi, xj) говорит, что ребро g инцидентно вершинам xi, xj и вершины xi, xj инцидентны ребру g.
№ 28
Какие две вершины в графе называются смежными?
• Две вершины xi, xj называются смежными, если они определяют ребро графа.
№ 29
Что такое ноль-граф?
• Ноль-графом называется граф, состоящий из изолированных вершин.
№ 30
Какое ребро графа называется ориентированным?
• Ребро графа называется ориентированным, если порядок расположения его концов (направление стрелок) в графе является существенным.
№ 31
Какой граф называется смешанным?
• Граф называется смешанным, если он содержит как ориентированные, так и неориентированные ребра.
№ 32
Граф U(x), ребрами которого являются всевозможные пары g(xi, xj) для двух возможных xi, xj ∈ X, i≠j называется:
• полным неориентированным графом.
№ 33
Что такое элементарная цепь?
• Цепь, в которой ни одна из вершин не повторяется.
№ 34
Для каких графов определены такие понятия, как путь и контур?
• Для ориентированных графов.
№ 35
Определение симметрического графа?
• Граф называется симметрическим, если любые две смежные вершины графа xi, xj соединены неориентированными ребрами.
• Граф называется симметрическим, если любые две смежные вершины графа xi, xj соединены противоположно ориентированными дугами.
№ 36
Какой граф изображен на рисунке справа по отношению к графу, изображенному на рисунке слева?
#ris36.JPGris
• Частичный граф.
№ 37
Какой граф изображен на рисунке справа по отношению к графу, изображенному на рисунке слева?
• Частичный подграф.
№ 38
Какие вершины называются связными?
• Две вершины xi, xj называются связными, если существует цепь S с концами xi, и xj.
№ 39
Сколько компонент сильной связности имеет граф, изображенный на рисунке?
• Две.
№ 40
Какой граф называется деревом?
• Деревом называется конечный связный неориентированный граф, состоящий по крайней мере из двух вершин и не содержащий циклов.
№ 41
Какой из двух графов, изображенных на рисунке, является плоским?
• Только а).
№ 42
Какие из графов, изображенных на рисунке, являются изоморфными?
• Все графы изоморфны.
№ 43
Как должен выглядеть граф G(X), соответствующий рефлексивному отношению?
• Граф G(X) должен иметь петлю в каждой своей вершине.
№ 44
Как должен выглядеть граф G(X), соответствующий антисимметричному отношению?
• Все ребра графа G(X) должны быть ориентированными.
№ 45
Как должен выглядеть граф G(X), соответствующий транзитивному отношению?
• Граф G(X) должен обладать следующими свойствами: для любой пары ребер (дуг) графа (xi, xj), (xj, xk) должно иметься замыкающее ребро (дуга) (xi, xk).
№ 46
Как должен выглядеть граф G(X), соответствующий антирефлексивному отношению?
• Граф G(X) ни в одной из вершин не должен иметь петли.
№ 47
Как должен выглядеть граф G(X), соответствующий симметричному отношению?
• Все ребра графа G(X) должны быть неориентированными.
№ 48
Как должен выглядеть граф G(X), соответствующий тождественному отношению?
• Граф G(X) должен быть ориентированным и иметь петлю в каждой своей вершине.
№ 49
Какому отношению соответствует изображенный на рисунке граф?
• Отношению квазипорядка.
№ 50
Какому отношению соответствует изображенный на рисунке граф?
• Отношению строгого порядка.
№ 51
Какая матрица задается описанным ниже способом?
Пусть g1,...,gm – дуги, а x1,...,xn – вершины ориентированного графа G(X). Матрица S = || sij || (i = 1, …, n – номер вершины графа, j = 1, …, m – номер дуги графа), такая что:
| sij= { | 1, если gj исходит из xi, |
| -1, если gj заходит в xi, | |
| 0, если gj не инцидентна xi, |
№ 52
Какая матрица задается описанным ниже способом?
Пусть g1,...,gm – дуги, а x1,...,xn – вершины неориентированного графа G(X). Матрица В = || bij || (i = 1, …, m; j = 1, …, m, где m – число ребер графа), такая что:
| bij={ | 1, если ребра gi и gj имеют общий конец, |
| 0, в противном случае. |
№ 53
Какой граф называется пересечением двух графов G1(X) и G2(X), заданных на одном и том же множестве вершин?
• Граф, состоящий из ребер, принадлежащих и G1(X), и G2(X).
№ 54
Какой граф называется композицией двух графов G1(X) и G2(X), заданных на одном и том же множестве вершин?
• Граф, у которого множество вершин, смежных с вершиной xi, состоит из всех вершин, достижимых из xi цепью длины два, первое ребро которой принадлежит G2(X), а второе – G1(X).
№ 55
Какой граф называется суммой двух графов G1(X) и G2(X), заданных на одном и том же множестве вершин?
• Граф, состоящий из ребер, принадлежащих G1(X), либо G2(X).
№ 56
Какой граф называется суммой двух графов G1(X) и G2(X), заданных на различных множествах вершин?
• Граф, для которого справедливо Х = Х1 ∪ Х2 и G(xj) = G1(xj) ∪ G2(xj).
№ 57
Сколько компонент связности будет иметь граф, являющийся декартовым произведением двух графов, изображенных на рисунке?
• Две.
№ 58
Какой степенью будут обладать вершины графа, являющегося декартовой суммой двух графов, изображенных на рисунке?
• Три.
№ 59
На рисунке изображены два графа и одна из их композиций G(X). Какая композиция изображена на рисунке?
• G(X)=G2(G1(X)).
№ 60
Закончите фразу: “В конечном графе число вершин с нечетной степенью...”
• четно.
№ 61
Граф, степени всех вершин в котором равны, называется:
• однородным.
№ 62
Что для ориентированного графа означает формула:
![]()
• Полустепень исхода вершины xi равна сумме числа дуг, входящих во все вершины графа из вершины xi.
№ 63
Формула ![]()
для неориентированного графа характеризует:
• Расстояние между вершинами xi и xj.
№ 64
Формула 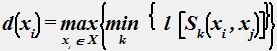
для ориентированного графа характеризует:
• Отклоненность вершины xi.
№ 65
Формула 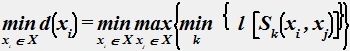
для ориентированного графа характеризует:
• Радиус графа.
№ 66
Формула
![]()
для ориентированного графа характеризует:
• Отклонение вершины xi от вершины xj.
№ 67
Формула 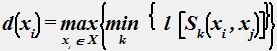
для неориентированного графа характеризует:
• Удаленность вершины xi.
№ 68
Дана матрица отклонений:
| X1 | X2 | X3 | X4 | |
| X1 | 4 | 2 | 3 | 1 |
| X2 | 5 | 2 | 2 | 1 |
| X3 | 3 | 2 | 4 | 3 |
| X4 | 4 | 1 | 1 | 5 |
• 2.
№ 69
Дана матрица отклонений:
| X1 | X2 | X3 | X4 | |
| X1 | 4 | 2 | 2 | 1 |
| X2 | 3 | 2 | 1 | 3 |
| X3 | 2 | 1 | 2 | 2 |
| X4 | 4 | 3 | 1 | 4 |
• 4.
№ 70
Дана матрица отклонений:
| X1 | X2 | X3 | X4 | |
| X1 | 4 | 2 | 3 | 1 |
| X2 | 5 | 2 | 2 | 1 |
| X3 | 3 | 2 | 4 | 3 |
| X4 | 4 | 1 | 1 | 5 |
• X1.
№ 71
Дана матрица отклонений:
| X1 | X2 | X3 | X4 | |
| X1 | 4 | 2 | 2 | 1 |
| X2 | 3 | 2 | 1 | 3 |
| X3 | 2 | 1 | 2 | 2 |
| X4 | 4 | 3 | 1 | 4 |
• X3.
№ 72
На рисунке изображен граф. Каждое ребро графа имеет вес, обозначенный соответствующим числом. С помощью алгоритма Дейкстры определите все кратчайшие пути от вершины X1 ко всем остальным вершинам.
• X2 – 8, X3 – 8, X4 – 5, X5 – 6.
№ 73
Конечный связный неориентированный мультиграф является эйлеровым графом тогда и только тогда:
• когда в нем отсутствуют вершины нечетной степени.
№ 74
В связном графе будет существовать эйлерова цепь тогда и только тогда:
• когда в нем все вершины имеют четную степень, за исключением начальной и конечной вершин.
№ 75
В конечном связном неориентированном графе G(X) с k вершинами нечетной степени минимальное число непересекающихся по ребрам цепей, покрывающих G(X) равно:
• k/2.
№ 76
Чтобы в конечном ориентированном графе существовал эйлеров цикл (контур), необходимо и достаточно, чтобы полустепени исхода и захода вершин этого графа по входящим и исходящим дугам удовлетворяли следующему соотношению:
• m´(xi)=m´´(xj), ∀xi∈X.
№ 77
В полном конечном графе всегда существует:
• Гамильтонов путь.
№ 78
Гамильтоновой цепью в неориентированном графе называется:
• цепь, проходящая через каждую его вершину один и только один раз.
№ 79
Пусть G(X) – неориентированный граф, имеющий n вершин, m ребер и r компонент связности. Цикломатическим числом графа G называется число ν(G)=
• m – n + r.
№ 80
Числом внутренней устойчивости можно назвать:
• наибольшее количество вершин графа, не смежных между собой.
№ 81
Числом внешней устойчивости можно назвать:
• наименьшее количество вершин графа, которые в совокупности смежны со всеми остальными вершинами.
№ 82
Чему равно число внутренней устойчивости для графа, имеющего вид куба?
• 4.
№ 83
Чему равно число внешней устойчивости для графа, имеющего вид куба?
• 2.
№ 84
Чему равен радиус графа, имеющего вид куба?
• 3.
№ 85
Чему равно число внутренней устойчивости для графа, имеющего вид октаэдра?
• 2.
№ 86
Чему равно число внешней устойчивости для графа, имеющего вид октаэдра?
• 2.
№ 87
Чему равен радиус графа, имеющего вид октаэдра?
• 2.
№ 88
Три поссорившихся соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу?
• Нет.
№ 89
Каково число ребер в полном неориентированном графе с n вершинами?
• n(n-1)/2.
№ 90
Какие из графов трех правильных многогранников имеют эйлеровы циклы?
• Октаэдр.
№ 91
Перечислите по порядку операции над высказываниями, имеющие следующие обозначения:
А→В, ∨(А,В), А∼В, А, ∧(А,В) ?
• Импликация, дизъюнкция, эквивалентность, отрицание, конъюнкция.
№ 92
Высказывание, которое истинно тогда и только тогда, когда А и В оба истинны или оба ложны, называется:
• эквивалентностью высказываний А и В.
№ 93
Высказывание, истинное только в том случае, когда А и В истинны, называется:
• конъюнкцией высказываний А и В.
№ 94
Высказывание, которое истинно, когда А ложно, и ложно, когда А истинно, называется:
• отрицанием высказывания А.
№ 95
Высказывание, которое ложно тогда и только тогда, когда А истинно, а В ложно, называется:
• импликацией высказываний А и В.
№ 96
Высказывание, которое истинно, если хотя бы одно из высказываний А или В является истинным, называется:
• дизъюнкцией высказываний А и В.
№ 97
Являются ли равносильными следующие формулы:
∧((X→Y),(X→Z)) и X→(∧(Y,Z)) ?
• Да.
№ 98
Являются ли равносильными следующие формулы:
X→(Y→Z) и (∧(X,Y))→ Z) ?
• Нет.
№ 99
Чему равно количество входных наборов для булевой функции n переменных?
• 2n.
№ 100
Чему равно количество различных булевых функций n переменных, задаваемых k различными наборами?
• 2k.
№ 101
Какая элементарная булева функция двух переменных задается следующей таблицей истинности?
| x1 | 0 | 0 | 1 | 1 |
| x2 | 0 | 1 | 0 | 1 |
| f(x1,x2) | 0 | 1 | 1 | 1 |
№ 102
Какая элементарная булева функция двух переменных задается следующей таблицей истинности?
| x1 | 0 | 0 | 1 | 1 |
| x2 | 0 | 1 | 0 | 1 |
| f(x1,x2) | 0 | 1 | 1 | 0 |
№ 103
Какая из приведенных ниже формул, характеризующих свойства элементарных функций, неверна?
• 5.
№ 104
Функция f(x1, x2, x3) принимает единичные значения на наборах №№ 0, 1, 3, 4, 6, 7. Какое количество конъюнкций будет иметь совершенная ДНФ этой функции?
• Шесть.
№ 105
Функция f(x1, x2, x3) принимает единичные значения на наборах №№ 0, 2, 4, 5, 7. Какое количество дизъюнкций будет иметь совершенная КНФ этой функции?
• Три.
№ 106
Функция f(x1, ...,xn) называется не сохраняющей ноль, если она:
• на наборе из нулей принимает значение 1.
№ 107
Функция f(x1, ...,xn) называется сохраняющей единицу, если она:
• на наборе из единиц принимает значение 1.
№ 108
Является ли самодвойственной следующая элементарная булева функция?
| x1 | 0 | 0 | 1 | 1 |
| x2 | 0 | 1 | 0 | 1 |
| f(x1,x2) | 0 | 1 | 0 | 0 |
№ 109
Является ли монотонной следующая элементарная булева функция?
| x1 | 0 | 0 | 1 | 1 |
| x2 | 0 | 1 | 0 | 1 |
| f(x1,x2) | 0 | 1 | 0 | 1 |
№ 110
Является ли линейной следующая элементарная булева функция?
| x1 | 0 | 0 | 1 | 1 |
| x2 | 0 | 1 | 0 | 1 |
| f(x1,x2) | 0 | 0 | 1 | 0 |
№ 111
Для того, чтобы система булевых функций была полна, необходимо и достаточно, чтобы она содержала функцию:
• не сохраняющую 0; не сохраняющую 1; несамодвойственную; немонотонную; нелинейную.
№ 112
Является ли полной система булевых функций, состоящая из сложения по модулю два, константы 1 и эквивалентности?
• Нет.
№ 113
Является ли полной система булевых функций, состоящая из константы 0 и импликации?
• Да.
№ 114
Является ли полной система булевых функций, состоящая из одной функции – стрелки Пирса?
• Да.
№ 115
Какой термин математической логики определяется следующей формулой:![]() ,
,
где все xij (j = 1,...,r) – различны, и если выполнено соотношение Ui→f(x1,...,xn)≡1 ?
• Импликант.
№ 116
Какая ДНФ получается дизъюнкций всех простых импликантов функции f(x1,...,xn) ?
• Сокращенная ДНФ.
№ 117
В чем состоит операция неполного склеивания?
• В замене выражения ∨(Ax,Ax) на ∨(∨(Ax,Ax), A).
№ 118
В чем состоит операция поглощения?
• В замене выражения ∨(AB,A) на A.
№ 119
Как называется импликант функции f(x1,...,xn), обладающий следующим свойством: элементарная конъюнкция, получающаяся из него удалением любой буквы, не является импликантом функции?
• Простой импликант.
№ 120
Как называется импликант функции f(x1,...,xn), обладающий следующим свойством: существует набор α=(α1,...,αn), на котором этот импликант обращается в 1, а все остальные импликанты сокращённой ДНФ - в ноль?
• Ядерный импликант.
№ 121
Что означает термин “тупиковая ДНФ” функции f (x1,...,xn)?
• ДНФ, из которой нельзя удалить ни одного простого импликанта.
№ 122
Перечислите по порядку этапы минимизации ДНФ.
• Нахождение сокращенной ДНФ, нахождение тупиковых ДНФ, выбор минимальной ДНФ.
№ 123
Верно ли утверждение: “Дизъюнкция всех ядерных импликантов любой функции f(x1,...,xn) представляет собой ее минимальную ДНФ”?
• Нет.
№ 124
Как обозначаются столбцы импликантной таблицы при минимизации ДНФ методом Квайна?
• Элементарными конъюнкциями.
№ 125
Функция f(x1,x2,x3) принимает единичные значения на наборах №№ 1, 2, 3, 5, 6. Сколько букв будет иметь совершенная ДНФ данной функции?
• Пятнадцать.
№ 126
Функция f(x1,x2,x3) принимает единичные значения на наборах №№ 0, 2, 5, 6, 7. Сколько букв будет иметь сокращенная ДНФ данной функции?
• Восемь.
№ 127
Функция f(x1,x2,x3) принимает единичные значения на наборах №№ 1, 2, 5, 6, 7. Сколько тупиковых ДНФ будет найдено на этапе минимизации данной функции?
• Две.
№ 128
Функция f(x1,x2,x3) принимает единичные значения на наборах №№ 0, 1, 3, 6, 7. Сколько букв будет иметь минимальная ДНФ данной функции?
• Шесть.
№ 129
Функция f(x1,x2,x3) принимает единичные значения на наборах №№ 0, 2, 3, 6, 7. Какова минимальная ДНФ данной функции?
• ∨(x2,x1x3).
№ 130
Что представляет собой множество вершин графа переходов при автоматном описании некоего объекта?
• Множество внутренних состояний системы.
№ 131
Для какого автомата составляется таблица переходов?
• Для автомата с памятью.
№ 132
Какой элемент при построении логической схемы имеет следующее обозначение?
• Конъюнкция.
№ 133
Минимальная ДНФ имеет вид: ∨(x3,x1)x2. Сколько логических элементов будет иметь логическая схема данной минимальной ДНФ в базисе, состоящем только из элементов {V, }?
• Четыре.
№ 134
Минимальная ДНФ имеет вид: ∨(x3,x1)x2. Сколько логических элементов будет иметь логическая схема данной минимальной ДНФ в базисе, состоящем только из элементов {∧( , ), }?
• Шесть.
№ 135
Какое множество называется полем предиката P(x1, x2,.., xn)?
• Множество M1×M2×...Mn (декартово произведение) множеств значений предметных переменных.
№ 136
Применимы ли к предикатам все операции алгебры высказываний?
• Да.
№ 137
Что означает символ ∀ ?
• Квантор общности.
№ 138
Высказывание, истинное только в том случае, когда предикат Р (х) истинен хотя бы для одного предмета из поля М, обозначается выражением:
• ∃xP(x).
№ 139
Являются ли равносильными следующие формулы логики предикатов: ∀xW(x) и ∃xW(x) ?
• Нет.
№ 140
Дано высказывание А: “Существуют четные простые числа”. Укажите отрицание высказывания А:
• “любое простое число нечетно”
№ 141
Является ли тавтологией формула: ∧((X→Y),X) → Y ?
• Да.
| на главную | база по специальностям | база по дисциплинам | статьи |
Другие статьи по теме
