Специальные главы математики. Часть 2.
Теория графов
Пермякова
Томск-2000

Основные понятия и определения.

№ 1
Граф без петель называется
• мультиграфом.

№ 2
В орграфе G вершина x смежна вершине y если
• в графе G есть дуга (x,y).

№ 3
В орграфе G вершина x инцидентна дуге v если
• вершина x либо начало дуги v, либо конец дуги v.

№ 4
Для любого неорграфа истинно выражение “Если вершина x смежна вершине y, то и вершина y смежна вершине x”
• Да.

№ 5
В любом произвольном неорграфе число вершин нечетной степени
• всегда четно.

№ 6
Дан граф G:

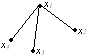
Чему равна степень вершины x1?
• 3

№ 7
Дан орграф G:

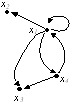
Чему равна полустепень захода вершины x1?
• 2

№ 8
Для любого орграфа всегда истинно выражение “Любая вершина графа смежна сама себе”
• Нет.

№ 9
Дан орграф G:

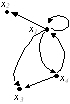
Чему равна полустепень исхода вершины x1?
• 4

№ 10
Граф с петлями и кратными ребрами называется
• псевдографом.

№ 1
Дан граф G

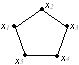
и граф G1

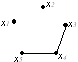
• граф G1 - суграф графа G;
• граф G1 - собственный подграф графа G.

№ 2
Дан граф G:

• граф G не является двудольным графом.

№ 3
Число ребер полного графа на n вершинах равно:
• (n*(n-1)) / 2.

№ 4
Граф K_2,3 изображен на рисунке

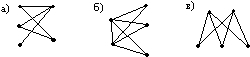
• в

№ 5
Дан граф G

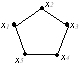
и граф G1

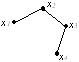
• граф G1 - собственный подграф графа G.

№ 6
Дан граф G

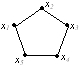
и граф G1

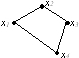
• граф G1 - результат стягивания графа G.

№ 7
Орграф G

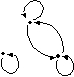
представляет отношение, обладающее свойствами
• рефлексивности, транзитивности, симметричности.

№ 8
Орграф G

представляет бинарное отношение, являющееся отношением
• строгого порядка.

№ 9
Транзитивное замыкание графа G

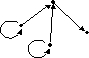
представлено на рисунке

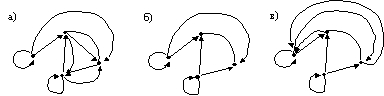
• б

№ 10
Сколько пар элементов содержит бинарное отношение, заданное графом G?

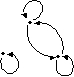
• 5

Представление графов в ЭВМ.

№ 1
Матрица смежности произвольного неорграфа есть
• квадратная симметричная матрица, элементы главной диагонали которой равны нулю.

№ 2
Матрица A(n× n) (n - количество вершин графа), элементы которой определяются следующим образом

называется:
• матрицей смежности.

№ 3
Дана матрица смежности

A=	0	1	1	0
	1	1	0	0
	0	1	1	1
	1	1	1	0

Граф, по которому построена матрица смежности является
• орграфом.

№ 4
Дана матрица смежности неорграфа G

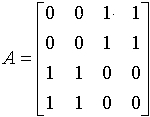
Сколько вершин и сколько ребер в графе G?
• 4; 4

№ 5
Дана матрица инцидентности орграфа G

Чему равны полустепени захода и исхода вершины x₃?
• 2; 2

№ 6
Матрица инцидентности неорграфа G(X,V), |X|= 7, |V|= 4 есть
• матрица В(7x4).

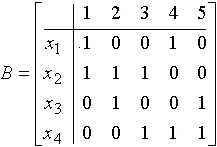
№ 7
Дан неорграф G

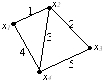
Выберите его матрицу инцидентности:
•

№ 8
Дан неорграф G(X,V), |X|= 3, |V|= 5. Чему равна размерность одного из массивов, составляющих список ребер графа?
• 10

№ 9
Выберите структуру смежности, соответствующую графу

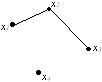
• x₁ : x₂;
x₂ : x₃, x₁;
x₃ : x₂;
x₄ :

№ 10
Матрица B(nxm)(n - количество вершин графа, m- количество ребер графа), элементы которой определяются следующим образом

bij={	1, если вершина i инцидентна ребру j;
	0, в противном случае

называется:
• матрицей инцидентности неорграфа.

Изоморфизм и планарность.

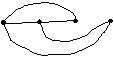
№ 1
Графы, изоморфные графу G

•
•

№ 2
Плоские графы
•
•

№ 3
Планарные графы
•
•
•

№ 4
Сколько подграфов нужно построить, чтобы проверить, планарен ли граф с n вершинами (по критерию Понтрягина-Куратовского)?
• C_n⁵.

№ 5
Сколько подграфов нужно построить, чтобы проверить, планарен ли граф с числом вершин, равным 7?
• 21

№ 6
Сколько подграфов нужно построить, чтобы проверить, планарен ли граф с числом вершин, равным 8?
• 56

№ 7
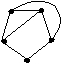
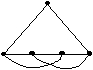
Выберите все графы, изоморфные графу G

•
•

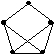
№ 8
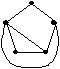
Плоские графы
•
•

№ 9
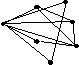
Планарные графы
•
•
•
•

Маршруты на графах. Основные понятия и определения. Эйлеровы цепи и циклы.

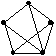
№ 1
Маршрут в орграфе, конечная и начальная вершина которого совпадают, называется
• контуром.

№ 2
Является ли путь M₁=x₁x₂x₃x₁x₄ простым путем?
• Нет.

№ 3
Дан неорграф G

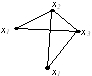
Укажите простой путь и простой цикл, построенный на графе G.
• M₂=x₁x₂x₃x₁;
• M₃=x₁x₃x₄x₂.

№ 4
Маршрут в неорграфе, конечная и начальная вершина которого совпадают, называется
• циклом.

№ 5
Маршрут в орграфе, конечная и начальная вершина которого не совпадают, называется
• путем.

№ 6
Маршрут в неорграфе, конечная и начальная вершина которого не совпадают, называется
• цепью.

№ 7
Дан неорграф G

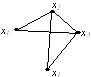
Укажите путь и цикл, построенные на графе G и не являющиеся простыми.
• M₁=x₁x₂x₄x₃x₂x₃;
• M₃=x₁x₃x₄x₃x₁.

№ 8
Эйлеровым циклом называется
• цикл, проходящий по всем ребрам графа ровно по одному разу.

№ 9
Для того, чтобы в графе существовала эйлерова цепь необходимо и достаточно, чтобы
• ровно две вершины имели нечетные степени.

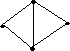
№ 10
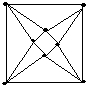
Выберите графы, которые можно изобразить, не отрывая руки от бумаги:
•
•
•

Связность графа

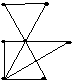
№ 1
Бинарное отношение, описываемое орграфом G, имеет следующие классы эквивалентности K₂=K₃=K₄={2,3,4},K₁={1}. Будет ли такой орграф сильносвязным?
• Нет.

№ 2
Чему равно число компонент связности графа G?

• 3

№ 3
Дан орграф G

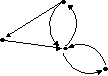
Орграф G
• слабо связный.

№ 4
Сколько “сильных компонент” имеет граф G?

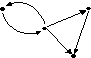
• 3

№ 5
Каркасом графа G

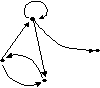
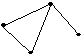
является граф, изображенный на рисунке
•

№ 6
Сколько “сильных компонент” имеет граф G?

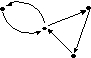
• 1

№ 7
Дан орграф G

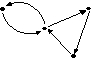
Орграф G
• сильно связный.

№ 8
Дан орграф G

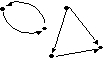
Орграф G
• не связный.

№ 9
Чему равно число компонент связности графа G?

• 2

№ 10
Чему равно число компонент связности графа G?

• 4

Понятие достижимости и взаимодостижимости.

№ 1
Дан неорграф G

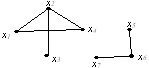
Чему равно множество достижимости вершины x₁?
• R_x1={x₁,x₄,x₂,x₃}.

№ 2
Найдите множество контрдостижимости вершины x₃ графа G:

• R_x3^-1={x₁,x₂x₃,x₄}.

№ 3
Отношение взаимодостижимости на графе есть
• отношение эквивалентности.

№ 4
Матрица достижимости связного неорграфа есть
• матрица, все элементы которой - единичные.

№ 5
Элементы матрицы взаимодостижимости s_ij орграфа могут быть получены следующим образом: (a_ij - элементы матрицы смежности, r_ij - элементы матрицы достижимости, q_ij - элементы матрицы контрдостижимости)
• s_ij=r_ij,q_ij.

№ 6
Дан орграф G

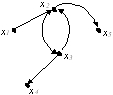
Матрица достижимости орграфа G может быть вычислена по формуле:
• R=E+A+A²+A³.

№ 7
Сколько компонент связности имеет неорграф, заданный своей матрицей достижимости

R=	1	0	1	1	0
	0	1	0	0	1
	1	0	1	0	0
	1	0	0	1	1
	0	1	0	1	1

• 2

№ 8
Найдите множество достижимости вершины x₃ графа G:

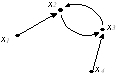
• R_x3={x₂,x₃}.

№ 9
Найдите множество контрдостижимости вершины x₂ графа G:

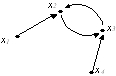
• R_x2^-1={x₁,x₂x₃,x₄}.

№ 10
Найдите множество достижимости вершины x₄ графа G:

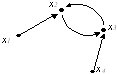
• R_x4={x₂x₃,x₄}.

Метрики связного неорграфа.

№ 1
Дан неорграф G

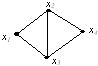
Диаметр графа G равен:
• 2

№ 2
Дан неорграф G

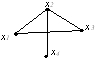
Радиус графа G равен:
• 1

№ 3
Неорграф G задан матрицей минимальных расстояний

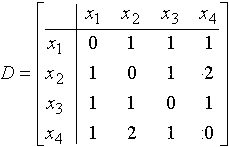
Центрами графа G являются вершины:
• x₁x₃.

№ 4
Дан неорграф G

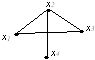
Диаметр графа G равен:
• 2

№ 5
Неорграф G задан матрицей минимальных расстояний

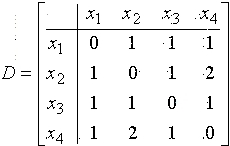
Чему равен диаметр графа G?
• 2

№ 6
Неорграф G задан матрицей минимальных расстояний

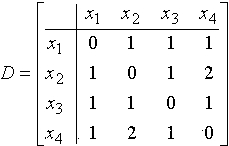
Чему равен радиус графа G?
• 1

№ 7
Дан неорграф G

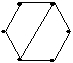
Чему равен диаметр графа?
• 3

№ 8
Дан неорграф G

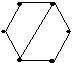
Чему равен радиус графа?
• 2

№ 9
Дан неорграф G

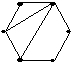
Чему равен диаметр графа?
• 3

№ 10
Дан неорграф G

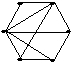
Чему равен радиус графа?
• 1

Алгоритмы на графах.

№ 1
Для выделения компонент связности можно использовать
• алгоритм обхода графа “в глубину”.

№ 2
Минимальный путь в неорграфе между заданными вершинами x и y может быть найден с помощью
• волнового алгоритма.

№ 3
Дан неорграф G

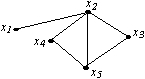
Для отыскания минимального пути из вершины x₁ в вершину x₅ использовали волновой алгоритм. Во фронт волны какого уровня войдет вершина x₅?
• 2

№ 4
Для поиска минимального пути в нагруженном орграфе между заданными вершинами x и y используется
• алгоритм Форда.

№ 5
Алгоритм Дейкстры ищет минимальный путь между заданными вершинами x и y
• и в нагруженном орграфе и в нагруженном неорграфе.

№ 6
Вершины дерева G

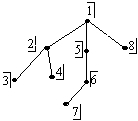
размечены с помощью алгоритма:
• обхода дерева “в глубину”.

№ 7
Дан граф G

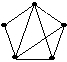
и его остовное дерево Т

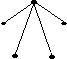
Остовное дерево Т построено при помощи
• обхода дерева “в ширину”.

№ 8
Вершины дерева G

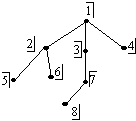
размечены с помощью алгоритма:
• обхода дерева “в ширину”.

№ 9
Дан граф G

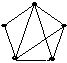
и его остовное дерево Т

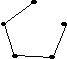
Остовное дерево Т построено при помощи
• обхода дерева “в глубину”.

№ 10
Дан неорграф G

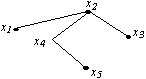
Для отыскания минимального пути из вершины x₁ в вершину x₅ использовали волновой алгоритм. Во фронт волны какого уровня войдет вершина x₅?
• 3

Деревья.

№ 1
Сколько можно построить различных деревьев на пяти вершинах?
• 125

№ 2
Сколько ребер в дереве с пятью вершинами?
• 4

№ 3
В произвольном дереве можно выделить
• только простую цепь.

№ 4
Дано дерево G

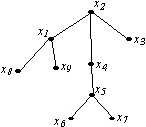
Правильные высказывания:
• x₈,x₉,x₇ - листы дерева;
• x₂ - корень дерева;
• x₂,x₄,x₅ - ствол дерева.

№ 5
Между выбранными двумя вершинами x и у произвольного дерева можно построить:
• единственную простую цепь.

№ 6
В любом дереве
• хотя бы две висячие вершины.

№ 7
Число различных деревьев, построенных на n вершинах равно
• n^n-2.

№ 8
Дан код дерева G К=(1,1,2,3). Сколько вершин в дереве G?
• 6

№ 9
Дано дерево G

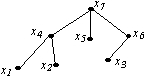
Запишите код дерева (через запятую).
• 4,4,6,7,7

№ 10
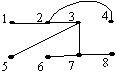
Дан код дерева К=(2,2,3,3,7,7). Данному коду соответствует дерево
•

Остовные деревья. Цикломатика графа.

№ 1
Цикломатическое число графа G

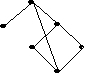
равно
• 2

№ 2
Связность графа не меняется при удалении
• циклового ребра.

№ 3
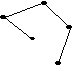
Выберите графы, являющиеся остовными деревьями графа G

•
•

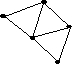
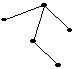
№ 4
Сколько ребер необходимо удалить из графа G

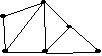
для получения остовного дерева?
• 4

№ 5
Нагруженный граф задан матрицей весов

Минимальный остов графа содержит ребра:
• (x₅,x₃)(x₅,x₁)(x₁,x₂)(x₅,x₄).

№ 6
Цикломатическое число графа не меняется при удалении
• перешейка.

№ 7
Дан неорграф G

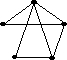
Каково количество циклов, входящих в независимый базис?
• 3

№ 8
Дан неорграф G

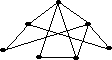
Каково количество циклов, входящих в независимый базис?
• 4

№ 9
Сколько ребер необходимо удалить из графа G

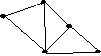
для получения остовного дерева?
• 5

№ 10
Неорграф задан матрицей смежности

Сколько ребер в остовном дереве графа?
• 4