Дискретная математика. Часть 2
(ГОС 1995г)
Дискретная математика (ГОС 2000г)
(ГОС 2000г)
для специальностей 210100, 220300
Жигалова Е.Ф.
Томск-2004
№ 1
Конечный связный граф, имеющий эйлеров цикл называются эйлеровыми.
№ 2
Эйлеров контур - это эйлеров цикл в конечном ориентированном графе.
№ 3
Эйлеров цикл - это простой цикл в конечном связном неориентированном графе, содержащий все рёбра графа.
№ 4
Гамильтоновым циклом в неориентированном связном графе называется цикл, проходящий через каждую вершину один и только один раз за исключением начальной вершины, которая совпадает с конечной.
№ 5
Гамильтоновой цепью в неориентированном связном графе называется цепь, проходящая через каждую вершину один и только один раз.
№ 6
Каркас графа G=(X,U) - это суграф графа G, не имеющий циклов и с тем же числом компонент связности, что и у графа G.
№ 7
Дерево это - связный неориентированный граф G=(X,U), не содержащий циклов и имеющий не менее двух вершин.
№ 8
Граф G=(X,U) называется двудольным, или бихроматическим, если множество вершин Х можно разбить на два подмножества Х1 и Х2, которые между собой не пересекаются, их объединение равно множеству Х, а вершины, принадлежащие одному тому же подмножеству, между собой не смежны.
№ 9Обыкновенный граф - это неориентированный униграф без петель.
№ 10
Дополнительным графом для обыкновенного графа G=(X,U) называется обыкновенный граф с с тем же множеством вершин Х и множеством ребер, в которое не входят ребра из U, и которые дополняют граф G=(X,U) до полного.
№ 11
Максимальный пустой подграф графа G=(X,U).
• Это пустой подграф G'=(X',U') графа G=(X,U), такой, что X´ ⊆ X и U´ ⊆ U, и G'=(X',U') не является подграфом никакого другого большего максимального пустого подграфа графа G=(X,U).
№ 12
Образуют ли подмножества вершин {(x1,x3),(x4,x3),(x1,x4),(x2,x3)} графа G(X,U), где
, семейство максимальных пустых подграфов?
• Нет, так как подграфы данного семейства подграфов являются полными.
• Нет, так как вершины в указанных подмножествах являются смежными.
№ 13
Клика графа.
• Это полный подграф G'=(X',U') графа G=(X,U), такой, что X´ ⊆ X и U´ ⊆ U.
№ 14
Определить, образуют ли подмножества вершин {(x1,x2),(x1,x2,x3),(x1,x3,x4),(x4,x3),(x2,x3,x4)} графа G(X,U), где
, семейство максимальных полных подграфов?
• Нет, так как подмножество (x1,x2) входит в (x1,x2,x3), а подмножество (x4,x3) входит (x1,x3,x4) и (x2,x3,x4).
• Нет, так как для данного графа максимальными полными подграфами являются подграфы, образованные вершинами (x1,x3,x4) и (x1,x2,x4).
№ 15
Максимальный полный подграф данного графа.
• Это полный подграф G'=(X',U') графа G=(X,U), такой, что X´ ⊆ X, U´ ⊆ U и G'=(X',U') не является подграфом никакого другого большего максимального полного подграфа данного графа.
№ 16
Определение понятия “метрика графа”.
• Метрика графа это расстояния (отклонения) между вершинами графа G(X). Метрика определяется аксиомами:
а) ρ(xi),(xj)=ρ(xj),xi);
б) ρ(xi),(xj)+ρ(xj,xz)≥ρ(xi,xz).
• Метрика графа это расстояния (отклонения) между вершинами графа G(X). Метрика определяется аксиомами:
а) ρ(xi),(xj)≥0;
б) ρ(xi),(xj)=0⇒xi=xj.
№ 17
Правила построения скелета
графа G=(X,U), заданного матрицей смежности A=(aij).
• ∀aij, i=j приравнять к нулю.
• ∀aij>1 приравнять к единице.
• Для всех i,j сделать aij=aji.
№ 18
Раскраска графа. Хроматическое число. Дать определение.
• Раскраска графа - это такое приписывание цветов (натуральных чисел) вершинам графа, что никакие две смежные вершины не получают одинаковый цвет (одно и тоже число). Хроматическое число - это наименьшее возможное число цветов в раскраске.
№ 19
Связность графа. Компонента связности. Дать определения.
• Граф G(X) связен, если любая пара его вершин может быть связана простой цепью. Компонента связности - это наибольший связный подграф графа G(X).
№ 20
Дать определение информационной (транспортной) сети (ИТС).
• ИТС это связный ориентированный граф G(X,U), у которого есть вершина xk∈X такая, что Гxk=∅ и вершина xi∈X такая, что Г¯xi=∅.
№ 21
Для графа G(X,U), где 
Написать минимальное выражение П произведения логических переменных x1, x2, x3, x4, позволяющее выделить подмножества вершин графа G, образующих все его максимальные пустые подграфы.
При вписывании ответа соблюдать следующие требования:
1. Переменные в сомножителях записывать в порядке возрастания их номеров.
2. Слагаемые записывать в порядке возрастания номеров входящих в них сомножителей и числа переменных.
Ответ: (П=x1x3+x1x2x4+x2x3x4)
№ 22
Для графа G(X,U), где
Написать минимальное выражение П произведения логических переменных x1, x2, x3, x4, позволяющее выделить подмножества вершин графа G, образующих все его максимальные полные подграфы.
При вписывании ответа соблюдать следующие требования:
1. Переменные в сомножителях записывать в порядке возрастания их номеров.
2. Слагаемые записывать в порядке возрастания номеров входящих в них сомножителей и числа переменных.
Ответ: (П=x2+x4)
№ 23
Найти все максимальные пустые подграфы графа G(X,U), где
Ответ в виде последовательности вершин, образующих максимальные пустые подграфы данного графа.
Ответ: (x1;x4;x2x3.)
№ 24
Найти все максимальные полные подграфы графа G(X,U), где
Ответ в виде последовательности вершин, образующих максимальные полные подграфы данного графа.
Ответ: (x1x2x4;x1x3x4.)
№ 25
Для графа G(X,U), где
Найти все максимальные полные подграфы.
Ответ в виде последовательности вершин, образующих максимальные полные подграфы данного графа.
Ответ: (x1x2x3;x1x3x4.)
№ 26
Для графа G(X,U), где
Найти все максимальные пустые подграфы.
Ответ в виде последовательности вершин, образующих максимальные пустые подграфы данного графа.
Ответ: (x1;x3;x2x4.)
№ 27
Определить есть ли маршрут длины L=3 между вершинами x1,x6 в графе G=(X,U), где
Найти матрицу смежности А в соответствующей степени k, указать значение степени k.
• 
№ 28
Определить число t маршрутов длины L=3 между вершинами x2,x6 в графе G=(X,U), где
и перечислить их, указывая в порядке возрастания номера вершин через которые маршрут проходит.
• t=7; M2,6={(2,1,2,6),( 2,3,2,6), (2,3,4,6),(2,6,1,6),(2,6,2,6),(2,6,4,6),(2,6,5,6)}.
№ 29
Построить все маршруты М длины L=3 на орграфе 
, где
.
Найти матрицу смежности А в соответствующей степени k (порядок перечисления - по строкам), указать значение степени k.
• M={x1,x4,x2,x3},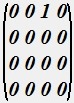 
, значение степени k=3.
№ 30
Определить число t маршрутов длины L=3 между вершинами x1-x2 в графе G=(X,U), где.
В ответе число маршрутов и соответствующая степень m матрицы смежности А.
Ответ: (4;3)
№ 31
Построить все маршруты М, связывающие вершину x1 с вершиной x3 длиной L=3 на орграфе , где
.
Найти матрицу смежности А в соответствующей степени k.
• M={(x1x1x1x3),(x1x1x2x3),(x1x1x3x3),(x1x1x4x3),(x1x2x3x3),(x1x3x3x3),(x1x4x3x3)}, значение степени k=3.
№ 32
Построить все маршруты М, связывающие вершину x1 с вершиной x2 длиной L=3 на орграфе , где.
Найти матрицу смежности А в соответствующей степени k.
• M={(x1x1x1x2),(x1x1x3x2)}, значение степени k=3.
№ 33
Построить все маршруты М, связывающие вершину x4 с вершиной x3 длиной L=3 на орграфе , где.
Найти матрицу смежности А в соответствующей степени k.
• M={(x4x2x3x3),(x4x3x3x3)}, значение степени k=3.
№ 34
Построить все маршруты М, связывающие вершину x1 с вершиной x3 длиной L=2 на орграфе , где
.
Найти матрицу смежности А в соответствующей степени k.
• M={(x1x2x3),(x1x4x3),(x1x1x3),(x1x3x3)}, значение степени k=2, значение элемента a42k=0 (матрицы А).
№ 35
Построить все маршруты М, связывающие вершину x1 с вершиной x3 длиной L=2 на орграфе , где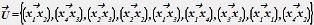
.
Найти матрицу смежности А в соответствующей степени k.
• M={(x1x1x3),(x1x2x3),(x1x4x3),(x1x3x3)}, значение степени k=2, значение элемента a12k=3 (матрицы А).
№ 36
Построить скелет графа G=(X,U), где 
.
Записать множество рёбер скелета 
по аналогии с записью рёбер U.
• 
.
№ 37
Для графа 
, где 
.
Построить дополнительный граф 
.
Ответ в виде последовательности рёбер множества 
.
• 
№ 38
Для графа , где 
.
Построить дополнительный граф .
Ответ в виде последовательности рёбер множества .
• =∅
№ 39
Построить скелет графа G=(X,U), где
.
Ответ в виде последовательности рёбер множества 
.
• 
.
№ 40
Определить: граф , где 
, относится к классу обыкновенных графов?
• Нет
№ 41
Укажите рёбра, которые нужно удалить из графа G=(X,U), где , чтобы он стал относиться к классу обыкновенных графов. Рёбро записывать парой инцидентных ему вершин
• (x2x3),(x3x2),(x3x3),(x3x4),(x4x3),(x4x4).
№ 42
Определить: граф G=(X,U), заданный матрицей смежности А с элементами:
a11=0,a12=1,a13=1,a14=1,
a21=1,a22=0,a23=2,a24=1,
a31=1,a32=2,a33=1,a34=2,
a41=1,a42=1,a43=2,a44=1, относится к классу обыкновенных графов?
• Нет
№ 43
Построить скелет графа G=(X,U), где .
Записать матрицу смежности А графа .
• 
№ 44
Для графа , где 
,
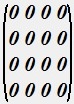
построить дополнительный граф и записать его матрицу смежности А.
• 
№ 45
Раскрасить граф G=(X,U), применяя метод Магу, если 
. Определить:
а) хроматическое число γ(G);
б) все максимальные пустые подграфы P(G) методом Магу;
в) множества вершин K(G), которым можно приписать одно и тоже натуральное число(цвет).
• γ(G)=3;
P(G)={x2x3,x1x3x6,x1x4x6,x1x4x7,x2x4x7,x2x5x7,x1x3x57};
K(G)={x2,x4x6,x1x3x5x7},{x6,x2x4,x1x3x5x7}.
№ 46
Для графа G(X,U), где .
Определить:
а) хроматическое число γ(G);
б) все максимальные пустые подграфы P(G) методом Магу;
в) множества вершин K(G), которым можно приписать одно и тоже натуральное число(цвет).
• γ(G)=3;
P(G)={x1,x3,x2x4};
K(G)={x1,x3,x2x4}.
№ 47
Для графа G(X,U), где .
Определить:
а) хроматическое число γ(G);
б) все максимальные пустые подграфы P(G) методом Магу;
в) множества вершин K(G), которым можно приписать одно и тоже натуральное число(цвет).
• γ(G)=3;
P(G)={x1,x4,x2x3};
K(G)={x1,x4,x2x3}.
№ 48
Для графа G(X,U), где 
.
Определить:
а) хроматическое число γ(G);
б) все максимальные пустые подграфы P(G) методом Магу;
в) множества вершин K(G), которым можно приписать одно и тоже натуральное число(цвет).
• γ(G)=4;
P(G)={x1,x2,x3,x4};
K(G)={x1,x2,x3,x4}.
№ 49
Раскрасить граф G=(X,U), применяя метод Магу, если . Определить:
а) хроматическое число γ(G);
б) все максимальные пустые подграфы P(G) методом Магу;
в) множества вершин K(G), которым можно приписать одно и тоже натуральное число(цвет).
• γ(G)=4=3;
P(G)={x1x3x6,x1x4x6,x1x4x7,x2x4x7,x2x5x7,x1x3x5x7};
K(G)={x2,x4x6,x1x3x5x7},{x6,x2x4,x1x3x5x7}.
№ 50
Для графа G(X,U), где .
Определить:
а) хроматическое число γ(G);
б) все максимальные пустые подграфы P(G) методом Магу;
в) множества вершин K(G), которым можно приписать одно и тоже натуральное число(цвет).
• γ(G)=3;
P(G)={x1,x3,x2,x4};
K(G)={x1,x3,x2,x4}.
№ 51
Для графа G(X,U), где .
Определить:
а) хроматическое число γ(G);
б) все максимальные пустые подграфы P(G) методом Магу;
в) множества вершин K(G), которым можно приписать одно и тоже натуральное число(цвет).
• γ(G)=3;
P$(G)={x1,x4,x2,x3};
K$(G)={x1,x4,x2,x4}.
№ 52
Для графа G(X,U), где 
. Определить:
а) хроматическое число γ(G);
б) все максимальные пустые подграфы P(G) методом Магу;
в) множества вершин K(G), которым можно приписать одно и тоже натуральное число(цвет).
• γ(G)=3;
P(G)={x1,x3,x2,x4};
K(G)={x1,x3,x2,x4}.
№ 53
Раскрасить граф G=(X,U), применяя метод Магу, если 
.
Определить:
а) хроматическое число γ(G);
б) все максимальные пустые подграфы P(G) методом Магу;
в) множества вершин K(G), которым можно приписать одно и тоже натуральное число.
• γ(G)=3;
P(G)={x1x3x6,x1x4x6,x1x4x7,x2x4x7,x2x5x7,x1x3x5x7};
K(G)={x2,x4x6,x1x3x5x7},{x6,x2x4,x1x3x5x7}.
№ 54
Раскрасить граф G=(X,U) , применяя метод Магу, если 
. Определить:
а) хроматическое число γ(G);
б) все максимальные пустые подграфы P(G) методом Магу;
в) множества вершин K(G), которым можно приписать одно и тоже натуральное число(цвет).
• γ(G)=3;
P(G)={x2x3x5x6,x2x3x5x7,x2x3x4x6x7,x1x3x4x5x6,x1x3x4x6x7,x1x2x4x5x6,x1x2x4x5x7,x1x2x4x6x7};
K(G)={x2x5,x3x6,x1x4x7},{x2x5,x3x7,x1x4x6}.
№ 55
Определить число компонент связности K(G) графа G=(X,U), где
U={(x1x2),(x3x4),(x2x3),(x4x5),(x2x6),(x5x6),(x6x7),(x8x9),(x10x11),(x11x10),(x10x9),(x9x10),(x8x10),(x8x11),(x9x11)}.
Ответ: (2)
№ 56
Определить число компонент связности H(G) графа G=(X,U), где
U={
,
,
} и показать, как изменятся номера вершин после отождествления вершины x2 с вершиной x5.
• H=2; 1-1,2-10,3-2,4-3,5-10,6-4,7-5,8-6,9-7,10-8,11-9.
№ 57
Определить:
1) число компонент связности K(G) графа , где ;
2) как изменятся номера вершин после отождествления вершины x3 с вершиной x1.
3) записать формулу для вычисления значения элемента a´33 матрицы смежности A´ графа G´, полученного из графа G после склеивания вершины x3 с вершиной x1.
• K(G)=1; 1-3,2-1,3-3,4-2; a´33=a11+a13+a31+a33.
№ 58
Определить:
1) число компонент связности K(G) графа #math , где 
;
2) как изменятся номера вершин после отождествления вершины x3 с вершиной x6.
• K(G)=3;1-1,2-2,3-9,4-3,5-4,6-9,7-5,8-6,9-7,10-8.
№ 59
Определить:
1) число компонент связности K(G) графа , где
2) как изменятся номера вершин после отождествления вершины x4 с вершиной x10.
3) записать формулу для вычисления значения элемента a´9,9 матрицы смежности A´ графа G´, полученного из графа G после склеивания вершины x4 с вершиной x10.
• K(G)=3;1-1,2-2,3-3,4-9,5-4,6-5,7-6,8-7,9-8,10-9; a´9,9=a4,10+a4,4+a10,4+a10,10.
№ 60
Определить:
1) число компонент связности K(G) графа , где ;
2) как изменятся номера вершин после отождествления вершины x4 с вершиной x10.
3) записать формулы для вычисления значений элементов a´i,9 (i=1,9) матрицы смежности A´ графа G´, полученного из графа G после склеивания вершины x4 с вершиной x10.
• K(G)=3;1-1,2-2,3-3,4-9,5-4,6-5,7-6,8-7,9-8,10-9; a´1,9=a1,4+a1,10, a´2,9=a2,4+a2,10, a´3,9=a3,4+a3,10, a´4,9=a5,4+a5,10, a´5,9=a6,4+a6,10, a´6,9=a7,4+a7,10, a´7,9=a8,4+a8,10, a´8,9=a9,4+a9,10, a´9,9=a4,4+a4,10+a10,10.
№ 61
Определить:
1) число компонент связности K(G) графа , где 
;
2) как изменятся номера вершин после отождествления вершины x2 с вершиной x4;
3) вычислить значение элемента a´33 матрицы смежности A´ графа G´, полученного из графа G после склеивания вершины x2 с вершиной x4.
• K(G)=1;1-1,2-3,3-2,4-3; a´33=3.
№ 62
Определить:
1) число компонент связности K(G) графа , где ;
2) как изменятся номера вершин после отождествления вершины x2 с вершиной x3;
3) вычислить значение элемента a´33 матрицы смежности A´ графа G´, полученного из графа G после склеивания вершины x2 с вершиной x3.
• K(G)=1;1-1,2-3,3-3,4-2; a´33=2.
№ 63
Определить:
1) число компонент связности K(G) графа , где ;
2) как изменятся номера вершин после отождествления вершины x2 с вершиной x4;
3) записать формулу для вычисления значения элемента a´33 матрицы смежности A´ графа G´, полученного из графа G после склеивания вершины x4 с вершиной x10.
• K(G)=1;1-1,2-3,3-2,4-3; a´33=a22+a24+a42+a44.
№ 64
Определить число компонент связности K(G) графа G=(X,U),где
U={,
,
} и показать, как изменятся номера вершин после отождествления вершины x7 с вершиной x5.
• K(G)=2; 1-1,2-2,3-3,4-4,5-10,6-5,7-10,8-6,9-7,10-8,11-9.
| Тема: 8. Транспортные сети. |
№ 65
Определить, является ли граф G(X,U) транспортной сетью, если U={
}.
• НЕТ, так как есть xi∈X такая, что Г¯xi=∅ и нет xk∈X такой, что Гxk=∅.
№ 66
Определить, является ли граф G(X,U) транспортной сетью, если
.
• НЕТ, так как есть xk∈X такая, что Гxk=∅ и нет xi∈X такой, что Г¯xi=∅.
№ 67
Определить, является ли граф G(X,U) транспортной сетью, если 
.
• НЕТ, так как есть xk∈X такая, что Гxk=∅ и нет xi∈X такой, что Г¯xi=∅.
• Данный граф содержит дугу - петлю.
№ 68
Обозначим интерпретирующий транспортную сеть граф - , а поток на ней θ(u), исток - х0, сток - z, c(u) пропускная способность. Поток θ(u) на транспортной сети это целочисленная функция, заданная на множестве дуг графа и удовлетворяющая свойствам. Определите какие это свойства.
• сумма потоков на дугах входящих в вершину х (х ≠x0 и х ≠z) равна сумме потоков на дугах выходящих из вершины x.
• θ(u)<=c(u).
• θ(u)>=0.
№ 69
Определить является ли поток на сети T максимальным, если интерпретирующий его граф G=(X,U) содержит дуги
(здесь за скобками нижний индекс соответствует пропускной способности, верхний - величине потока на дуге 
? При решении использовать процедуры алгоритма Форда-Фалкерсона.
Поток на сети Т максимальный , так как при разметке вершин вершину x6 пометить нельзя.
№ 70
Найти минимальный разрез T на сети , где (здесь за скобками нижний индекс соответствует пропускной способности, верхний - величине потока на дуге 
.
• 
.
№ 71
Вычислить значение максимального потока Фmax на сети 
, где за скобками нижний индекс соответствует пропускной способности, верхний - величине потока на дуге .
Ответ: (40)
№ 72
Вычислить значение максимального потока Фmax на сети 
, где за скобками нижний индекс соответствует пропускной способности дуги .
Ответ: (40)
№ 73
На сети , где число за скобками - пропускная способность дуги .
Oпределить значение максимального потока Фmax и насыщенные дуги.
• Фmax=40; #math {(x2x4),(x2x5),(x3x5),(x5x4),(x5x6)}.
№ 74
Вычислить значение максимального потока Фmax на сети , где за скобками нижний индекс соответствует пропускной способности, верхний - величине потока на дуге .
Ответ: (40)
№ 75
Дан граф , где 
.
Найти ошибки в матрице смежности R данного графа:
r11=0,r12=1,r13=1,r14=1,r15=0,r16=0,
r21=1,r22=1,r23=2,r24=0,r25=0,r26=0,
r31=1,r32=2,r33=0,r34=0,r35=0,r36=0,
r41=1,r42=1,r43=1,r44=0,r45=0,r46=0,
r51=0,r52=0,r53=0,r54=0,r55=0,r56=3,
r61=0,r62=0,r63=0,r64=0,r65=0,r66=0.
Выписать элементы матрицы R с неправильными значениями, придерживаясь последовательности их записи по строкам, и для них вписать верные значения.
• r21=0,r31=0,r41=0,r65=1.
№ 76
Дан граф , где .
Перечислить элементы матрицы смежности А данного графа (порядок перечисления - по строкам).
• А={a(1,1)=0, a(1,2)=1, a(1,3)=1, a(1,4)=1,
a(2,1)=0, a(2,2)=0, a(2,3)=1, a(2,4)=0,
a(3,1)=0, a(3,2)=0, a(3,3)=0, a(3,4)=0,
a(4,1)=0, a(4,2)=1, a(4,3)=1, a(4,4)=0}
№ 77
Дан граф , где 
.
Перечислить элементы матрицы смежности А данного графа (порядок перечисления - по строкам).
• А={a(1,1)=1, a(1,2)=1, a(1,3)=1, a(1,4)=1,
a(2,1)=0, a(2,2)=0, a(2,3)=1, a(2,4)=0,
a(3,1)=0, a(3,2)=0, a(3,3)=1, a(3,4)=0,
a(4,1)=0, a(4,2)=1, a(4,3)=1, a(4,4)=0}.
№ 78
Дан граф , где .
Перечислить элементы матрицы смежности А в степени 2 для данного графа (порядок перечисления - по строкам).
• А(2)={a(1,1)=1, a(1,2)=2, a(1,3)=4, a(1,4)=1,
a(2,1)=0, a(2,2)=0, a(2,3)=1, a(2,4)=0,
a(3,1)=0, a(3,2)=0, a(3,3)=1, a(3,4)=0,
a(4,1)=0, a(4,2)=0, a(4,3)=2, a(4,4)=0}.
№ 79
Дан граф , где .
Найдите матрицу смежности R данного графа.
• 
.
№ 80
Дан граф , где
Найдите матрицу смежности R данного графа.
• 
№ 81
Дан граф G=(X,U), где .
Найти матрицу смежности А данного графа.
• 
№ 82
Дан граф G=(X,U), где . Найти матрицу смежности А во второй степени для данного графа.
• 
№ 83
Дан граф G=(X,U), где . Найти матрицу смежности А логического типа во второй степени для данного графа.
• 
№ 84
Дан граф G=(X,U), где . Перечислить элементы матрицы инциденций А данного графа (порядок перечисления - по строкам). Рёбрам графа присвоить следующие номера:
.
• А={a(1,1)=1, a(1,2)=0, a(1,3)=0, a(1,4)=0, a(1,5)=0, a(1,6)=1, a(1,7)=0,
a(2,1)=1, a(2,2)=1, a(2,3)=0, a(2,4)=0, a(2,5)=0, a(2,6)=0, a(2,7)=1,
a(3,1)=0, a(3,2)=1, a(3,3)=1, a(3,4)=0, a(3,5)=0, a(3,6)=0, a(3,7)=0,
a(4,1)=0, a(4,2)=0, a(4,3)=1, a(4,4)=1, a(4,5)=0, a(4,6)=0, a(4,7)=0,
a(5,1)=0, a(5,2)=0, a(5,3)=0, a(5,4)=0, a(5,5)=1, a(5,6)=0, a(5,7)=0,
a(6,1)=0, a(6,2)=0, a(6,3)=0, a(6,4)=1, a(6,5)=1, a(6,6)=1, a(6,7)=1}.
№ 85
Определить в данном графе G=(X,U), где 
есть ли эйлеров цикл?
• Нет
№ 86
Определить в данном графе G=(X,U), где есть эйлеровa цепь?
Если эйлерова цепь есть, записать в круглых скобках цепь в форме последовательности номеров вершин (не отделяя их запятой), через которые она проходит, выбирая на каждом шаге вершину (из возможных) с меньшим номером.
• Да; (2142345265).
№ 87
Решить задачу коммивояжёра с матрицей расстояний D:
d12=4, d13=6, d14=2, d15=9,
d21=4, d23=3, d24=2, d25=9,
d31=6, d32=3, d34=5, d35=9,
d41=2, d42=2, d43=5, d45=8,
d51=9, d52=9, d53=9, d54=8.
Применить для решения алгоритм Литтла. В ответе указать длину (число) L найденного цикла и через точку с запятой сам цикл. Вершины перечислять в порядке их определения по алгоритму Литтла. В случае равного выбора - выбирать вершины с меньшим номером.
• 25;1-4-2-5-1.
№ 88
Определить в данном графе G=(X,U), где 
есть эйлерова цепь? Если эйлерова цепь есть, записать в круглых скобках цепь в форме последовательности номеров вершин, через которые она проходит, выбирая на каждом шаге вершину (из возможных) с меньшим номером.
• Да; (521432456276).
№ 89
Определить в данном графе G=(X,U), где есть эйлерова цепь.
Если эйлерова цепь есть, указать в круглых скобках через запятую начальную и конечную вершины эйлеровой цепи. Начальной вершине присвоить меньший номер.
• Да; (5,6).
№ 90
Определить в данном графе G=(X,U), где 
есть эйлерова цепь.
Если эйлерова цепь есть, записать в круглых скобках цепь в форме последовательности номеров вершин, через которые она проходит, выбирая на каждом шаге вершину (из возможных) с меньшим номером. Если эйлеровой цепи нет, то определить: есть ли в в данном графе эйлеров цикл.
• Есть цикл.
№ 91
Решить задачу коммивояжёра с матрицей расстояний D:
d12=24, d13=26, d14=22, d15=29,
d21=24, d23=23, d24=22, d25=29,
d31=26, d32=23, d34=25, d35=29,
d41=22, d42=22, d43=25, d45=28,
d51=29, d52=29, d53=29, d54=28.
Применить для решения алгоритм Литтла. В ответе указать длину (число) L найденного цикла и через точку с запятой сам цикл. Вершины перечислять в порядке их определения по алгоритму Литтла. В случае равного выбора - выбирать вершины с меньшим номером.
• (125;1-4-2-3-5-1.)
№ 92
Решить задачу коммивояжёра с матрицей расстояний D:
d12=14, d13=16, d14=12, d15=19,
d21=14, d23=13, d24=12, d25=19,
d31=16, d32=13, d34=15, d35=19,
d41=12, d42=12, d43=15, d45=18,
d51=19, d52=19, d53=19, d54=18.
Применить для решения алгоритм Литтла. В ответе указать длину (число) L найденного цикла и через точку с запятой сам цикл. Вершины перечислять в порядке их определения по алгоритму Литтла. В случае равного выбора - выбирать вершины с меньшим номером.
• (75;1-4-2-3-5-1.)
№ 93
Решить задачу коммивояжёра с матрицей расстояний D:
d12=19, d13=21, d14=17, d15=24,
d21=19, d23=18, d24=17, d25=24,
d31=21, d32=18, d34=20, d35=24,
d41=17, d42=17, d43=20, d45=23,
d51=24, d52=24, d53=24, d54=23.
Применить для решения алгоритм Литтла. В ответе указать длину (число) L найденного цикла и через точку с запятой сам цикл. Вершины перечислять в порядке их определения по алгоритму Литтла. В случае равного выбора - выбирать вершины с меньшим номером.
• (100;5-1-4-2-3-5.)
№ 94
Определить в данном графе G=(X,U), где 
, есть ли эйлеров цикл.
• Нет
| на главную | база по специальностям | база по дисциплинам | статьи |
Другие статьи по теме
