
Физика твердого тела. Часть 1.
Смирнов С.В.
Кафедра ФЭ
Томск-2001
№ 1
Величина волны Де Бройля:
• λ = h/p.
№ 2
Вероятность нахождения частицы в данном объёме определяет интеграл:
• ∫ (|Ψ|² dV).
№ 3
Полная энергия электрона:
• E = (p² / 2m) + U
№ 4
Потенциальная энергия электрона, находящегося на расстоянии r от заряда величиной +е:
• U = - e² / (4πε0r).
№ 5
Радиус Бора равен:
• диаметру атома водорода - 0,53 Å.
№ 6
Первый потенциал ионизации атома водорода:
• 13,6 эВ.
№ 7
Состояние электрона в атоме характеризуется квантовыми числами:
• n, l, ml, s.
№ 8
Интеграл перекрывания волновых функций:
• S = ∫ (ΨaΨb dV).
№ 9
Энергия, необходимая для удаления электрона из атома:
• потенциал ионизации.
№ 10
Энергия, освобождаемая при добавлении электрона к атому:
• сродство к электрону.
№ 11
Склонность атома притягивать обобществленные электроны:
• электроотрицательность.
№ 12
Максимальной электроотрицательностью обладают атомы элемента:
• F.
№ 13
Для атомов в структуре алмаза характерна гибридизация:
• sp³.
№ 14
Наибольшая энергия связи гибридизации:
• sp³d².
№ 15
На одну связывающую гибридизированную орбиталь приходится:
• 1/8 электронов каждого атома в кристалле Li.
№ 16
При образовании молекулы должно выполняться основное условие:
• минимум потенциальной энергии молекулы.
№ 17
Основные виды sp-гибридизации в порядке увеличения прочности связи:
• sp, sp², sp³, sp³ d².
№ 18
Пространственная конфигурация sp² - гибридизации:
• тетраэдрическая.
№ 19
Закон Брэгга:
• 2a sino = nλ.
№ 20
Условие интерференции Лауэ:
• a(coso-coso1) = mλ.
№ 21
Основные виды химической связи в порядке возрастания энергии:
• водородная, металлическая, ковалентная, ионная.
№ 22
Решетка Бравэ:
Это трехмерная решетка образованная всеми точками с радиусами-векторами R вида
• R = n1a+n2b+n3c.
№ 23
Если a,b и с вектора прямой решетки, то вектора обратной решетки равны:
• ![]() .
.
№ 24
Если объём прямой решетки V = a × b × c, то объём обратной решетки ω равен
• ω = (2π)³ / V.
№ 25
Сколько существует точечных групп, которые может иметь решетка Бравэ и сколько существует решеток Бравэ:
• 7 и 14.
№ 26
Зона Бриллюэна:
• ячейка Вигнера-Зейтца в обратной решетке.
№ 27
В элементарной ячейке алмаза находится:
• 8 атомов.
№ 28
Поверхность Ферми:
• поверхность постоянной энергия ЕF электронов в ḱ - пространстве.
№ 29
Уровень Ферми:
• максимальная энергия электронов в кристалле при 0° К.
№ 30
Электроны в кристалле меди имеют энергию Ферми:
• 7,04 эВ.
№ 31
Стоячая волна:
• периодическое синфазное колебание с характерным чередованием узлов (нулей) и пучностей (максимумов).
№ 32
Волновой вектор:
• k′ = π/λ
№ 33
Модуль волнового вектора ḱ на границах области длиной а существования стоячей волны (узел или пучность) принимает значение:
• ḱ = πn/a, (где n=1,2,3...).
№ 34
Квазичастица:
• кванты элементарных возбуждений в кристалле.
№ 35
Квазиимпульс:
• p=ḱh
№ 36
Распределение фононов по энергиям описывается:
• функцией Бозе-Эйнштейна.
№ 37
Распределение электронов в твердых телах по энергиям:
• функцией Ферми-Дирака.
№ 38
Функция распределения Максвелла-Больцмана определяет:
• вероятность распределения частиц по энергиям.
№ 39
Вид математической формулы для распределения Ферми-Дирака.
• ![]() .
.
№ 40
- для распределения Бозе-Эйнштейна.
• ![]() .
.
№ 41
Минимальная частота колебаний цепочки одинаковых атомов длиной L и расстоянием между атомами а:
• ωмин = πv / L.
№ 42
Максимальная частота колебаний:
• ωмах = πvL / a.
№ 43
Минимальная частота колебаний акустических фононов в цепочке из двух типов атомов массой М1 и М2:
• ωакуст = √(2β/M1).
№ 44
Максимальная частота колебаний фононов в цепочке из двух типов атомов массой М1 и М2:
• ![]() .
.
№ 45
На единицу объёма к-пространства приходится стоячих волн:
• dnω = (ω²dω) / (π²v³3B).
№ 46
Удельная теплоемкость:
• Cv = dQ/dT.
№ 47
Средняя энергия тепловых колебаний атома в приближении гармонического осциллятора:
• kT
№ 48
Тепловые колебания атомов происходят с частотой:
• 1012 c-1.
№ 49
Алмаз имеет температуру Дебая OД° K:
• 1850.
№ 50
Формула для теплоемкости по закону Дюлонга-Пти:
• Cv = 3R.
№ 51
Характеристическая температура Эйнштейна:
• OЭ = hωЭ / k.
№ 52
Математическая формулировка закона Дебая.
• Cv = γДT³.
№ 53
Наиболее корректно описывает поведение теплоемкости при низких температурах:
• закон Дебая.
№ 54
Ангармонизм колебаний атомов в кристалле обусловлен:
• асимметрией зависимости энергии связи от межатомного расстояния.
№ 55
Ангармоническими эффектами обусловлены физические явления в кристаллах:
• теплопроводность и тепловое расширение.
№ 56
Коэффициент линейного теплового расширения:
• α = (Δl / l) (1 / ΔT).
№ 57
Закон распространения тепла Фурье:
• Q = -λgradT.
№ 58
Дебай установил связь теплопроводности с теплоемкостью формулой:
• λ = 1/3 v3B Cv СВ.
№ 59
Закон Видемана-Франца:
• (λ/σ) = LT.
№ 60
Сущность приближения Борна-Оппенгеймера:
• неподвижны только ядра.
№ 61
Сущность приближения Хартри-Фока:
• рассматривается движение одного электрона в поле, образованном другими электронами.
№ 62,63
Решением уравнения Шредингера при одноэлектронном приближении является функция Блоха:
• Ψ = U(r)exp(-iḱr).
№ 64
Модель Кронига-Пенни объясняет:
• существование разрешенных и запрещенных зон.
№ 65
Электрон, находящийся в валентной зоне, может участвовать в электропроводности:
• при наличие в валентной зоне свободных уровней.
№ 66
Материал, если у него все зоны заполнены электронами, возможно отнести к:
• диэлектрикам.
№ 67
Определить энергию свободного электрона, имеющего импульс р и массу m позволяет формула:
• 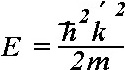
№ 68
Полное число состояний в первой зоне Бриллюэна равно:
• числу атомов в кристалле.
№ 69
Необходимо сдвинуть вторую зону Бриллюэна, чтобы привести её к первой зоне (а- период решетки), на величину:
• 2π/a.
№ 70
Эффективная масса m*n электрона:
•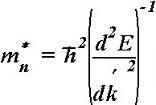
№ 71
Эффективная масса электрона в центре зоны Бриллюэна и на краях, имеет знак:
• положительная в центре, отрицательная на краях.
№ 72
Эффективная масса электронов в кремнии:
• 0.19m; 0,92m.
№ 73
Подвижность носителей заряда:
• коэффициент пропорциональности между дрейфовой скоростью и напряженностью электрического поля.
№ 74
Величина подвижности электронов:
• μ = e(τ) / mn*.
№ 75
Концентрация носителей в зоне проводимости:
• n = ∫( N(E) f(E,T) dE).
№ 76
Плотность состояний в зоне проводимости:
• N(E) = 4π(2m*n / h²)3/2 (E-Ec)1/2.
№ 77
Зависимость концентрации электронов в зоне проводимости от температуры:
• n = Nc exp [(Ec-Ef) / (kT)].
№ 78
Эффективная плотность состояний в зоне проводимости кремния:
• 2,8 1019 см-3.
№ 79
Зависимость уровня Ферми от температуры в собственном полупроводнике:
• Ef = (Ec+Ev)/2 + (kT/2)ln(Nv/Nc).
№ 80
Уровень Ферми в собственном полупроводнике при 0К находится:
• посредине запрещенной зоны.
№ 81
Уровень Ферми в вырожденном электронном полупроводнике:
• в зоне проводимости.
№ 82
Электропроводность собственного полупроводника:
• σ = e [nμn + μp].
№ 83
“Дырка” в полупроводнике:
• некоторая воображаемая частица с положительными зарядом и массой.
№ 84
В кремнии существует:
• 3 типа дырок.
№ 85
Закон действующих масс в физике твердого тела:
• n0p0 = n²i.
№ 86
Уровень Ферми в собственном полупроводнике при повышении температуры приближается:
• к зоне, где эффективная плотность состояний ниже.
№ 87
Концентрация электронов и дырок в собственном полупроводнике:
• ![]() .
.
№ 88
К точечным относятся дефекты:
• вакансии и атомы в междоузлиях.
№ 89
- к линейным:
• дислокации и трещины.
№ 90
Дефекты в ряд в порядке возрастания их размеров:
• точечные, линейные, объёмные.
№ 91
К образованию вакансий в кристалле приводят:
• дефекты Шоттки.
№ 92
- к образованию пары вакансия-междуузельный атом:
• дефекты Френкеля.
№ 93
Требует наличия в кристалле стоков:
• дефекты Шоттки.
№ 94
Равновесная концентрация дефектов Френкеля в кристалле (N0 - количество узлов, Nа - количество междоузлий):
• ![]() .
.
№ 95
F-центр:
• анионная вакансия с локализованным электроном.
№ 96
V-центр:
• катионная вакансия с локализованной дыркой.
№ 97
Облако Котрелла:
• скопление дефектов вокруг дислокации.
№ 98
1-ый закон Фика:
• j = - D ∂n/∂x.
№ 99
2-ой закон Фика:
• ∂n/∂t = (D∂²n) / (∂x²).
№ 100
Конфигурационная энтропия:
• S = k ln W.
| на главную | база по специальностям | база по дисциплинам | статьи |
Другие статьи по теме
