Имитационное моделирование экономических процессов
для специальности 080801
Мицель А.А.
Кафедра АСУ
Томск-2005

№ 1
Имитационное моделирование представляет собой:
• технику анализа выходных зависимых переменных моделей, в которых одна или несколько входных независимых переменных представляются случайными.

№ 2
В основе имитационного моделирования лежит:
• метод многократного решения задач “Что будет, если?”.

№ 3
Стохастические переменные - это:
• переменные, значения которых не могут быть точно установлены или предсказаны.

№ 4
Величина риска от принятия решения определяется, как потенциальные потери:
• среднее значение всех возможных потерь и выигрышей от данной операции.

№ 5
Какие из методов анализа риска принимаемых решений являются наиболее употребительными?
• Метод, основанный на определении наилучшего и наихудшего сценариев последствий решения.
• Mетод, основанный на решении задач типа “Что будет, если?”.
• Имитационное моделирование.

№ 6
Какую информацию нам дает базовый сценарий?
• Наиболее вероятное значение выходной переменной.

№ 7
Какую информацию не дает нам метод анализа наилучшего и наихудшего сценариев?
• О форме (законе) распределения вероятностей выходной переменной.

№ 8
К недостатку метода “Что будет, если...?” относят:
• невозможность определить закон распределения вероятностей выходной переменной.

№ 9
Метод решения задач типа “Что будет, если...?” заключается:
• в анализе риска путем расчета различных сценариев.

№ 10
Методом Монте-Карло называется:
• численные методы решения математических задач при помощи моделирования случайных величин.

№ 11
В основе вычислений по методу Монте-Карло лежит:
• случайный выбор чисел из заданного вероятностного распределения.

№ 12
Наиболее часто на практике используются следующие критерии проверки статистических гипотез.
• Kритерий χ² (хи-квадрат).
• Kритерий Крамера-фон Мизеса.
• Kритерий Колмогорова-Смирнова.

№ 13
При каких условиях наиболее предпочтительно использовать критерии χ²?
• Если объемы выборок N≥100, в отношении которых проводится анализ, велики.

№ 14
При каких условиях наиболее предпочтительно использовать критерии Колмогорова-Смирнова?
• Если объем выборок находится в интервале 10≤N≤100, в отношении которых проводится анализ.

№ 15
Датчиками или генераторами случайных чисел называют:
• специальные программы, входящих в состав программного обеспечения ЭВМ, или стандартные процедуры, функции, генерирующие случайные (точнее, псевдослучайные) величины.

№ 16
Пусть с помощью датчика случайных чисел, равномерно распределенных в интервале (0,1) выбрано некоторое число z, определим вероятность того, что z<P_A. Для случайной величины z с равномерным распределением справедлива следующая зависимость:
• P(z<P_A) =∫₀^PA f(x)dx = P_A.

№ 17
Пусть имеется случайная величина x с показательным распределением. Функция распределения имеет вид:
• F(x)=1-e^-λx.

№ 18
Если сделать предельный переход и устремить n→∞, то распределение случайной величины интервала t=T(k) в суммарном потоке событий, состоящем из k элементарных потоков, устремится к экспоненциальному закону с математическим ожиданием:
• .

№ 19
Моделирование случайных величин с произвольным распределением. Целесообразно выбрать величины a_k так, чтобы вероятности попадания в любой частичный интервал P_k были одинаковы, т. е.
• ∫_ak-1^ak f_k(x)dx = 1/n, (a_k=1,2,...,n).

№ 20
Что представляет собой сетевая модель?
• План выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети.

№ 21
Что подразумевается под термином действительная работа?
• Протяженный во времени процесс, требующий затрат ресурсов.

№ 22
Что означает термин событие в сетевой модели?
• Момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта.

№ 23
Дайте определение “пути” в сетевом графике.
• Это любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы.

№ 24
Какой путь в сетевом графике называется критическим?
• Наиболее продолжительный полный путь в сетевом графике.

№ 25
Упорядочение сетевого графика заключается:
• в таком расположении событий и работ, при котором для любой работы предшествующее ей событие расположено левее и имеет меньший номер по сравнению с завершающим эту работу событием.

№ 26
Частный резерв времени первого вида R₁ работы (i,j):
• часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события.

№ 27
Частный резерв времени второго вида - это:
• часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события.

№ 28
Независимый резерв времени R_н работы (i,j) -
• часть полного резерва времени, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие работы начинаются в ранние сроки.

№ 29
Для определения числовых характеристик t(i,j) и σ²(i,j)β - распределения для работы (i,j) на основании опроса ответственных исполнителей проекта и экспертов определяют три временные оценки:
• оптимистическую оценку t_опт(i,j), т.е. продолжительность работы (i,j) при самых благоприятных условиях;
• пессимистическую оценку t_пес(i,j), т.е. продолжительность работы (i,j) при самых неблагоприятных условиях;
• наиболее вероятную оценку t_нв(i,j), т.е. продолжительность работы (i,j) при нормальных условиях.

№ 30
Коэффициентом напряженности К_н работы (i,j):
• .

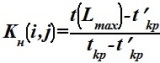№ 31
При использовании метода “время - стоимость” предполагают, что:
• уменьшение продолжительности работы пропорционально возрастанию ее стоимости.

№ 32
Оптимизация сетевого графика - это:
• процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения.

№ 33
Полный резерв времени R_n(i,j) работы (i,j) показывает:
• на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится.

№ 34
Важным свойством полного резерва времени работы является то, что:
• он принадлежит не только этой работе, но и всем полным путям, проходящим через нее.

№ 35
Какие этапы входят в процесс разработки и машинной реализации математической модели?
• Построение концептуальной модели, разработка алгоритма модели системы, разработка программы модели системы, проведение машинных экспериментов с моделью.

№ 36
На каком этапе процесса разработки и машинной реализации математической модели происходит обоснование выбора показателя и критериев эффективности?
• Построение концептуальной модели.

№ 37
Какие существуют способы построения моделирующих алгоритмов?
• Способ повременного моделирования с постоянным шагом, способ повременного моделирования с переменным шагом, способ последовательной проводки заявок, способ поэтапной последовательной проводки заявок.

№ 38
Если используется способ повременного моделирования, то какой прием позволяет повысить точность работы модели?
• Уменьшение шага ΔT.

№ 39
Каким достоинством обладает способ повременного моделирования?
• Способ позволяет моделировать любые процессы: детерминированные, непрерывные, случайные и т.д.

№ 40
Какой способ построения моделирующих алгоритмов позволяет моделировать систему, предназначенную для обслуживания заявок двух различных приоритетов?
• Способ поэтапной последовательной проводки заявок.

№ 41
В чем сущность второго этапа моделирования поэтапной последовательной проводки заявок?
• На данном этапе происходит моделирование обслуживания заявок второго приоритета в условиях, что на временной оси располагаются уже обслуженные заявки первого приоритета.

№ 42
Какой способ построения моделирующих алгоритмов позволяет моделировать в системе зависимые события?
• Способ повременного моделирования с постоянным и переменным шагом.

№ 43
В чем характерная особенность отказов первого рода?
• Они приводят к временному прекращению процесса обслуживания очередной заявки с сохранением достигнутого состояния.

№ 44
В чем характерная особенность взаимодействия периодов безотказной работы и периодов устранения отказов?
• Эти периоды не могут пересекаться и должны чередоваться.

№ 45
Чему равна плотность обобщенного потока Эрланга 2-го порядка?
• .

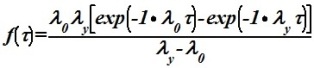№ 46
Что такое критерий эффективности?
• Правило, с помощью которого выбирается наиболее выгодный вариант структуры моделируемой системы.

№ 47
Что такое показатель эффективности?
• Мера степени достижения поставленной цели.

№ 48
Как нужно поступить, если в моделируемой системе массового обслуживания число каналов заранее неизвестно?
• Сделать число каналов переменным, т.е. включить его в состав входных параметров.

№ 49
Какой входной параметр позволяет определить вид текущего отказа при его формировании, если в системе могут возникать отказы первого и второго рода?
• Вероятность появления отказа первого рода.

№ 50
Чем характеризуется ''паутинообразная'' модель фирмы с обучением?
• Поставщики учитывают сложившуюся тенденцию изменения цен и с их учетом планируют, выпуск продукции на очередной отрезок времени.

№ 51
Как выглядит формула вычисления средневзвешенной цены в “паутинообразной” модели фирмы?
• P(ρ)=P_T-1- ρ(P_T-1-P_T-2).

№ 52
Что означает равенство весового коэффициента нулю в “паутинообразной” модели фирмы?
• Oбучение в модель не заложено.

№ 53
Как выглядит уравнение локального равновесия рынка?
• S_T=D_T+W_T.

№ 54
Что означает равенство числового фактора нулю в производственной модели фирмы?
• Время работы с изделием во всех цехах одинаково.

№ 55
Предметом теории массового обслуживания является:
• построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, характер потока заявок и т.п.) с показателями эффективности СМО, описывающими ее способность справляться с потоком заявок.

№ 56
Под случайным (вероятностным или стохастическим) процессом понимается:
• процесс изменения во времени состояния какой-либо системы в соответствии с вероятностными закономерностями.

№ 57
Случайный процесс называется марковским или случайным процессом без последствия, если:
• для любого момента времени вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент to и не зависят от того, когда и как система пришла в это состояние.

№ 58
Поток характеризуется интенсивностью λ:
• частотой появления событий или средним числом событий, поступающих в СМО в единицу времени.

№ 59
Поток событий называется потоком без последействия, если:
• для любых двух непересекающихся участков времени τ₁ и τ₂ - число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.

№ 60
Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно:
• стационарен, ординарен, регулярен и не имеет последействия.

№ 61
Свойство присущее только показательному распределению состоит в следующем:
• если промежуток времени, распределенный по показательному закону, уже длился некоторое время τ, то это никак не влияет на закон распределения части промежутка T-(τ/2): он будет таким же, как и закон распределения всего промежутка T.

№ 62
Какая система массового обслуживания называется многофазной?
• Cистема массового обслуживания, в которой процесс обслуживания требований состоит из нескольких этапов, выполняемых последовательно на различных обслуживающих устройствах.

№ 63
Сформулируйте правило составления уравнений Колмогорова.
• В левой части каждого из них стоит производная вероятности i - го состояния. В правой части - сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i - го состояния).

№ 64
Процесс гибели и размножения. Предельные вероятности вычисляются по следующим формулам для конечного числа состояний системы:
• ; ; ; .

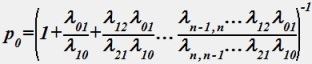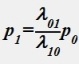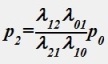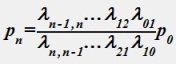№ 65
Утверждение:
• Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе (очереди) равно среднему числу заявок в системе (в очереди), деленному на интенсивность потока заявок.

№ 66
Предельная вероятность состояния S_i показывает:
• среднее относительное время пребывания системы в этом состоянии.

№ 67
Классическая задача Эрланга имеет следующую формулировку:
• имеется n каналов, на которые поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность μ. Найти предельные вероятности состояний системы и показатели ее эффективности.

№ 68
Для СМО с неограниченной очередью при ρ<1 любая заявка, пришедшая в систему, будет обслужена:
• то есть, вероятность отказа P_отк=0, относительная пропускная способность Q=1, а абсолютная пропускная способность равна интенсивности входящего потока заявок, то есть A=λ.

№ 69
Универсальным методом статистического моделирования называют:
• метод Монте-Карло.

№ 70
Идея метода Монте-Карло состоит в том, что:
• вместо аналитического описания СМО производится “розыгрыш” случайного процесса, проходящего в СМО, с помощью специально организованной процедуры.

№ 71
Формулой Уилсона или формулой наиболее экономичного объема партии является:
• .

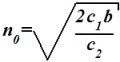№ 72
Какова вероятность того, что операция окажется неуспешной, т.е. ее доход будет меньше среднего ожидаемого дохода m?
• F(m).

№ 73
Рассчитайте среднюю ожидаемую доходность от операции Q, если

qi	5	10	6	4
pi	0,2	0,5	0,1	0,2

• 7,4

№ 74
Найдите риск операции (σ).

qi	5	10	6	4
pi	0,2	0,5	0,1	0,2

• 2,65

№ 75
Вероятность появления события А равна 0,35. Найдите вероятность того, что событие А не произойдет.
• 0,65

№ 76
Поток клиентов в супермаркете представляет собой пуассоновский поток с интенсивность 2 человека в минуту. z - случайная величина, равномерно распределенная на интервале (0,1). Определите, через сколько минут после открытия магазина появится первый покупатель, если z=0,45?
• 0,4

№ 77
Бензоколонка обслуживает поток машин. Время обслуживания представляет собой величину, равномерно распределенную на интервале (1,2). z - случайная величина, равномерно распределенная на интервале (0,1). Определите период обслуживания машины, если z=0,65.
• 1,65

№ 78
Мастерская занимается ремонтом обуви. Время, которое мастер тратит на обслуживание одного клиента распределено по нормальному закону с математическим ожиданием равным 1,5 и среднеквадратическим отклонением равным 1. z_i - случайные величины, равномерно распределенные на интервале (0,1). Определите время обслуживания заявки, если z₁=0,93; z₂=0,55; z₃=0,85; z₄=0,4; z₅=0,25; z₆=0,72; z₇=0,39; z₈=0,63; z₉=0,18; z₁₀=0,97; z₁₁=0,49; z₁₂=0,21.
• 1,65

№ 79
На предприятие поступают заявки на изготовление изделий. Поток этих требований представляет собой пуассоновский поток с интенсивностью 0,5 заявок в минуту. Время обслуживания распределено по показательному закону со средним значением равным 10 минутам. Определите, покинет ли следующая заявка данную систему не обслуженной, если предыдущая заявка начала обслуживание в 12:00, а ее обслуживание закончилось в 12:06; максимальное время ожидания равно 0,5 минут; z - случайная величина, равномерно распределенная на интервале (0,1). z=0,36.
• Заявка будет не обслужена.

№ 80
На телефонную станцию поступают звонки. Средняя продолжительность разговора равна 4 минуты. Вычислите интенсивность потока обслуживания.
• 0,25

№ 81
В одноканальную систему массового обслуживания поступает поток заявок с интенсивностью 0,5 заявок в минуту. Поток обслуживания имеет интенсивность 1 заявка в минуту. Определите относительную пропускную способность.
• 0,67

№ 82
В одноканальную систему массового обслуживания поступает поток заявок с интенсивностью 4 заявки в минуту. Поток обслуживания имеет интенсивность 3 заявки в минуту. Определите абсолютную пропускную способность.
• 1,71

№ 83
В многоканальной системе интенсивность входного потока равна 5 заявок в минуту, а интенсивность потока обслуживания равна 2 заявки в минуту. Вычислите интенсивность нагрузки канала.
• 2,5

№ 84
На аэродроме расположено 2 посадочные полосы. Если заняты обе полосы, то самолет не может приземлиться, и покидает аэропорт. Найдите вероятность того, что самолет покинет аэропорт, если интенсивность нагрузки посадочной полосы равна 1,2.
• 0,24

№ 85
В многоканальной системе массового обслуживания относительная пропускная способность равна 0,5. Определите среднее число занятых каналов, если интенсивность входного потока равна 4 заявки в минуту, а интенсивность обслуживания равна 1 заявка в минуту.
• 2

№ 86
В одноканальной системе массового обслуживания с неограниченной очередью интенсивность входного потока равна 0,3 заявки в минуту, а интенсивность обслуживания - 2 заявки в минуту. Определите среднее число заявок в очереди.
• 0,03

№ 87
В одноканальной системе массового обслуживания интенсивность входного потока равна 2 заявки в минуту. Какой должна быть интенсивность обслуживания, что бы очередь бесконечно росла?
• Меньше 2.

№ 88
В одноканальной системе массового обслуживания с неограниченной очередью интенсивность входного потока заявок равна 2 заявки в минуту. Определите среднее время пребывания заявки в системе, если среднее число заявок в системе равно 3.
• 1,5

№ 89
В одноканальной системе массового обслуживания с неограниченной очередью интенсивность входного потока заявок равна 4 заявки в минуту. Определите среднее время пребывания заявки в очереди, если среднее число заявок в очереди равно 2.
• 0,5

№ 90
В многоканальной системе массового обслуживания с неограниченной очередью интенсивность входного потока заявок равна 0,5 заявки в минуту, интенсивность обслуживания равна 4 заявки в минуту. Определите среднее число заявок в системе, если среднее число заявок в очереди равно 3.
• 3,13

№ 91
Вычислите критический путь графа, представленного на рисунке.

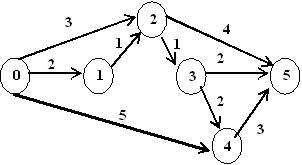
• 9

№ 92
По графу, изображенному на рисунке, вычислите резерв пути 0→1→3→4.

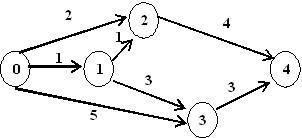
• 1

№ 93
Вычислите коэффициент напряженности работы (2,3) для сетевого графика на рисунке.

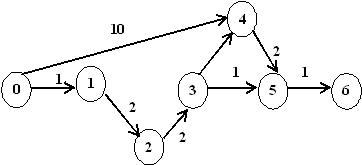
• 0,8

№ 94
Найдите вероятность того, что срок выполнения комплекса работ не превысит 15 суток, если: t _кр=14; σ_кр=10; Ф(0,1)=0,5398.
• 0,77

№ 95
Некоторая работа (i,j) имеет следующие оценки:
1. Оптимистическая: t_o(i,j)=2;
2. Пессимистическая: t_п(i,j)=4;
3. Наиболее вероятная: t_нв(i,j)=3.
Вычислите среднее значение продолжительности работы t(i,j).
• 3

№ 96
Потребность сборочного предприятия составляет 110 тыс. изделий в год. Эти детали расходуются в процессе производства равномерно и непрерывно. Детали заказываются раз в год и поставляются партиями одинакового объема, указанного в заказе. Хранение детали на складе обходится 0,5 д.е. за одну деталь в сутки. Затраты на доставку партии составляют 2000 д.е. Вычислите оптимальный объем одной партии (считать, что в году 365 дней).
• 1553

№ 97
Вычислите, насколько процентов увеличатся затраты на создание и хранение запаса, если оптимальный объем одной партии, равный 2000, увеличить до 2500.
• 3,1

№ 98
Предприятие закупает агрегат с запасными блоками к нему. Стоимость одного блока равна 10 д.е. В случае выхода агрегата из строя из-за поломки блока отсутствующего в запасе, простой агрегата, и срочный заказ нового блока к нему обойдется 130 д.е. Найдите плотность убытков из-за неудовлетворенного спроса (округлить до сотых).
• 0,93

№ 99
Потребность сборочного предприятия составляет 150 тыс. изделий в год. Эти детали расходуются в процессе производства равномерно и непрерывно. Детали заказываются раз в год и поставляются партиями одинакового объема, указанного в заказе. Оптимальный объем одной партии составляет 3300 деталей. Вычислите оптимальный интервал между поставками (считать, что в году 365 дней).
• 8,03

№ 100
Известно, что в модели управления запасами величина среднего ежедневного спроса равна 50, а среднеквадратическое отклонение ежедневного спроса равно 10. z_i - случайные величины, равномерно распределенные на интервале (0,1).Определите случайную величину дневного спроса, распределенную по нормальному закону, если z₁=0,93; z₂=0,62; z₃=0,54; z₄=0,41; z₅=0,35; z₆=0,78; z₇=0,27; z₈=0,66; z₉=0,49; z₁₀=0,23; z₁₁=0,91; z₁₂=0,39.
• 55,8