Информатика. Часть III
Кафедра ПрЭ
Четвергов К.В.
Томск-2001

№ 1
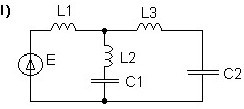
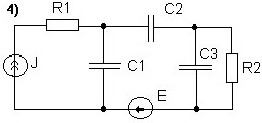
Топологически вырожденные схемы.
•
•

№ 2
Чему равен порядок системы дифференциальных уравнений математической модели электрической цепи?

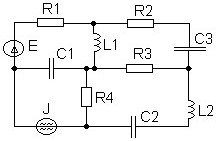
• 5

№ 3
Математическая модель линейной электрической цепи с постоянными параметрами, содержащей реактивные элементы, представляет собой:
• систему линейных дифференциальных уравнений с постоянными коэффициентами

№ 4
Для приведенной схемы электрической цепи указать переменные состояния

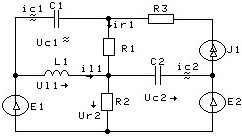
• ic1

№ 5
Для приведенной схемы электрической цепи указать входные переменные

• ic1

№ 6
Для приведенной электрической цепи составить уравнение для определения ic через переменные состояния

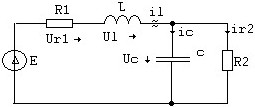
• il-0.2Uc

№ 7
Для приведенной электрической цепи составить уравнение для определения Ul через переменные состояния

• -2il-Uc+10

№ 8
Для приведенной электрической цепи составить уравнение для определения Ur1 через переменные состояния

• 2il

№ 9
Для приведенной электрической цепи составить уравнение для определения ir2 через переменные состояния

• 0.2Uc

№ 10
Для приведенной электрической цепи определить необходимое число уравнений по первому закону Кирхгофа

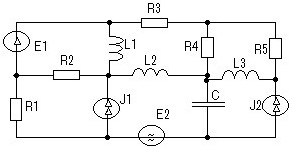
• 5

№ 11
Для приведенной электрической цепи определить необходимое число уравнений по второму закону Кирхгофа

• 4

№ 12
Какое из рекуррентных соотношений соответствует явной численной схеме Эйлера:
• x_k+1=x_k+hG_k

№ 13
Какое из рекуррентных соотношений соответствует неявной численной схеме Эйлера:
• x_k+1=(E-hA)^-1(x_k+hB)

№ 14
Какое из рекуррентных соотношений соответствует численной схеме трапеций:
• x_k+1=(2$E-hA)^-1[(2E+hA)x_k+2hB]

№ 15
Какое из представленных рекуррентных соотношений соответствует модифицированной численной схеме трапеций:
• x_k+1=x_k+|h/2|[G(t_k,x_k)+G(t_k+h,x_k+hG_k)]

№ 16
Какое из представленных рекуррентных соотношений соответствует численной схеме Рунге-Кутта четвертого порядка:
•

№ 17
Каким порядком аппроксимации обладает явная численная схема Эйлера?
• 1

№ 18
Каким порядком аппроксимации обладает неявная численная схема Эйлера?
• 1

№ 19
Каким порядком аппроксимации обладает численная схема трапеций?
• 2

№ 20
Каким порядком аппроксимации обладает модифицированная численная схема трапеций?
• 2

№ 21
Для математической модели dx/dt=-5x+b при x₀=0 и h=0.2 определить х₂ с помощью неявной численной схемы Эйлера.
• 0.15*N

№ 22
Для математической модели dx/dt=-5x+b при x₀=0 и h=0.4 определить х₂ с помощью численной схемы трапеций.
• 0.2*N

№ 23
Математическая модель электрической цепи имеет вид

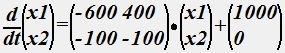
Определить постоянные времени τ₁ (в мс) и τ₂ (в мс).
• 2 5

№ 24
Математическая модель электрической цепи имеет вид

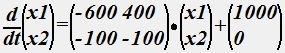
Определить время переходного процесса (в мс).
• 25

№ 25
Математическая модель электрической цепи имеет вид

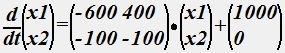
Определить постоянную времени (в мс).
• 10

№ 26
Математическая модель электрической цепи имеет вид

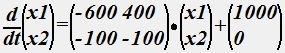
Определить круговую частоту собственных колебаний (в рад/c)
• 200

№ 27
Собственные числа матрицы А математической модели:
1) λ₁=-1000, λ₂=-2000
2) λ₁=-5000, λ₂=-2000
3) λ₁=1000, λ₂=-3000
4) λ₁=-3000, λ₂=-8000
В каком случае время переходного процесса максимально?
• 1

№ 28
Собственные числа матрицы А математической модели:
1) λ₁=-1000, λ₂=-2000
2) λ₁=-5000, λ₂=-2000
3) λ₁=1000, λ₂=-3000
4) λ₁=-3000, λ₂=-8000
В каком случае время переходного процесса минимально?
• 4

№ 29
Собственные числа матрицы А математической модели:
1) λ₁=-1000, λ₂=-2000
2) λ₁=-5000, λ₂=-2000
3) λ₁=1000, λ₂=-3000
4) λ₁=-3000, λ₂=-8000
В каком случае переходный процесс расходящийся?
• 3

№ 30
Для математической модели некоторой цепи

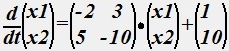
Определить установившееся состояние x1_c и x2_c.
• 8 5

№ 31
Для математической модели некоторой цепи

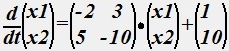
Определить постоянные интегрирования c1 и c2, если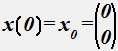
.
• -8 -5

№ 32
Из приведенных вариантов областей устойчивости численных схем выбрать соответствующий явной схеме Эйлера

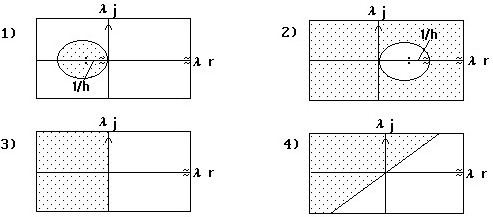
• 1

№ 33
Из приведенных вариантов областей устойчивости численных схем выбрать соответствующий неявной схеме Эйлера

• 2

№ 34
Из приведенных вариантов областей устойчивости численных схем выбрать соответствующий схеме трапеций

• 3

№ 35
Из приведенных вариантов областей устойчивости численных схем выбрать соответствующий условно устойчивой численной схеме

• 1

№ 36
Из приведенных вариантов областей устойчивости численных схем выбрать соответствующий абсолютно устойчивой численной схеме

• 2 3

№ 37
Для численной явной схемы Эйлера определить максимально возможный шаг интегрирования (h_max), если собственные числа матрицы А математической модели:
λ₁=-2000, λ₂=-1000.
• 0.001

№ 38
Для численной явной схемы Эйлера определить максимально возможный шаг интегрирования (h_max), если собственные числа матрицы А математической модели:
λ₁=-1000, λ₂=-500.
• 0.002

№ 39
Для численной явной схемы Эйлера определить максимально возможный шаг интегрирования (h_max), если собственные числа матрицы А математической модели:
λ₁=-200+j100, λ₂=-200-j100.
• 0.008

№ 40
Для численной явной схемы Эйлера определить максимально возможный шаг интегрирования (h_max), если собственные числа матрицы А математической модели:
λ₁=-1000+j2000, λ₂=-1000-j2000.
• 0.004

№ 41
Будет ли численная явная схема Эйлера устойчива, если собственные числа матрицы А математической модели λ₁-500+j500, λ₂=-500-j500, а шаг интегрирования h=0.003?
• нет

№ 42
Будет ли численная явная схема Эйлера устойчива, если собственные числа матрицы А математической модели λ₁=-500+j500, λ₂=-500-j500, а шаг интегрирования h=0.004? На сколько необходимо изменить шаг (Δh) интегрирования, чтобы схема стала устойчивой.
• 0.002

№ 47
Реализация математической модели - получение той или иной информации об объекте.

№ 52
В любой момент времени алгебраическая сумма токов в узле равна нулю. Укажите расшифрованное понятие.
• первый закон Кирхгофа

№ 53
В любой момент времени алгебраическая сумма ЭДС в контуре равна алгебраической сумме падений напряжения на элементах этого контура.
• второй закон Кирхгофа

№ 54
Алгебраическое уравнение, корни которого являются собственными чиcлами матрицы.
• характеристическое уравнение

№ 55
Величины, характеризующие скорость затухания свободной составляющей.
• постоянные времени

№ 56
Расстояние между соседними узлами сеточной области.
• шаг дискретизации

№ 57
Численные схемы, условия устойчивости которых зависят от величины шага интегрирования.
• условно устойчивые численные схемы

№ 58
Численные схемы, область устойчивости которых включает всю левую полуплоскость комплексной #mathlamda-плоскости.
• абсолютно устойчивые численные схемы