Компьютерное моделирование и проектирование электронных приборов и устройств
для специальности 200307
Саликаев Ю.Р.
Кафедра ЭП
Томск-2005

Вычислительный эксперимент. Представление чисел в ЭВМ.

№ 1
Выделите основополагающее понятие (0) и расставьте остальные в порядке следования (1-5) согласно схемы его построения:
•
0 - вычислительный эксперимент;
1 - объект исследования;
2 - математическая модель;
3 - численный метод;
4 - программа для ЭВМ;
5 - проведение вычислений и анализ результатов.

№ 2
Метод исследования, основанный на построении и анализе с помощью ЭВМ математических моделей (ММ) изучаемого объекта, называют вычислительный эксперимент.

№ 3
Основу схемы вычислительного эксперимента составляет триада: модель - метод (алгоритм) - программа.

№ 4
Как двоичная так и десятичная системы относятся к позиционным системам счисления.

№ 5
В позиционной системе с основанием r запись a=±a_n*a_n-1...a₀a_-1a_-2... означает, что a=±(a_nrⁿ+a_n-1*r^n-1+...+a₀*r⁰+a_-1*r^-1+a_-2*r^-2+...).

№ 6
При представлении чисел в форме с фиксированной запятой разрядная сетка делится на 3 части.

№ 7
При представлении чисел в форме с фиксированной запятой разрядная сетка отводится:
• в равной степени под целую и дробную части числа.

№ 8
При представлении чисел в форме с плавающей запятой разрядная сетка делится на 4 части.
• 4.

№ 9
При представлении чисел в форме с плавающей запятой разрядная сетка отводится:
• в большей степени под мантиссу числа.

№ 10
Число 103,67 в форме с плавающей запятой имеет порядок равный:
• 3.

Требования к вычислительным методам.

№ 11
Под численным методом понимается такая интерпретация ММ (“дискретная модель”), которая доступна для реализации на ЭВМ.

№ 12
Можно выделить две группы требований к численным методам. Первая группа связана с адекватностью дискретной модели исходной математической задаче, и вторая группа - с реализуемостью численного метода на ЭВМ.

№ 13
К группе требований к численным методам, связанных с адекватностью дискретной модели, относятся такие требования как устойчивость, корректность, сходимость.

№ 14
Задача называется устойчивой по исходному параметру х, если решение y непрерывно от него зависит. Другими словами, конечные, малые погрешности в исходной величине приводят к малым погрешностям в результате расчетов.

№ 15
Задачи, чувствительные к погрешностям исходных данных, называются неустойчивыми.

№ 16
Задача называется поставленной корректно, если для любых значений исходных данных из некоторого класса ее решение существует, единственно и устойчиво по исходным данным.

№ 17
Численный алгоритм (метод) называется корректным в случае существования и единственности численного решения при любых значениях исходных данных, а также в случае устойчивости этого решения относительно погрешностей исходных данных.

№ 18
Говорят, что итерационная последовательность сходится к точному решению x=a, если при неограниченном возрастании числа итераций предел этой последовательности существует и равен а:
. В этом случае имеем сходящийся численный метод.

№ 19
Под сходимостью разностного (сеточного, дискретного) метода понимается стремление значения решения разностной (дискретной) модели задачи к соответствующим значениям решения исходной задачи при стремлении к нулю параметра дискретизации.

№ 20
Правильно ли при оценке погрешности результатов полагаться на порядок погрешности исходных данных?
• Да, только для устойчивых задач.

Погрешности при вычислениях на ЭВМ.

№ 21
Погрешность результата вычисления суммы чисел на ЭВМ:
• минимизируется в случае суммирования от меньшего к большему.

№ 22
При вычислении на ЭВМ следует избегать:
• вычитания близких чисел.

№ 23
Различают два вида погрешностей - абсолютную и относительную. Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате его округления. Относительная погрешность - это отношение абсолютной погрешности к значению числа.

№ 24
Относительная точность в ЭВМ с плавающей запятой определяется числом разрядов t, отводимых для записи мантиссы.

№ 25
При сложении или вычитании чисел их абсолютные погрешности складываются. Относительная погрешность суммы заключена между наибольшим и наименьшим значением относительных погрешностей слагаемых; на практике принимается наибольшее значение.

№ 26
При умножении чисел друг на друга их относительные погрешности складываются. При делении чисел друг на друга их относительные погрешности складываются.

№ 27
Отметьте устранимые по отношению к численному методу погрешности.
• Погрешности метода.
• Погрешность дискретизации.

№ 28
В ЭВМ чаще всего используется представление чисел в форме с плавающей запятой, т.е. в виде a=M*r^p, где r - основание системы счисления, p - целое число (положительное, отрицательное или нуль) и r^-1≤“M”<1.

№ 29
Минимальное положительное число M₀, которое может быть представлено в ЭВМ с плавающей запятой называется машинным нулем.
Число M_∞=M₀^-1 называют машинной бесконечностью.

№ 30
Сколько разрядов сетки отводится под порядок числа, если максимально представимое число на этой сетке 2⁶³?
• 6.

Итерационные методы для систем нелинейных уравнений.

№ 31
Выберите метод, отличающийся областью применения.
• Метод Симпсона.

№ 32
Отметьте неверное утверждение. Метод Ньютона отличается от метода релаксации:
• точностью.

№ 33
Метод релаксации можно записать в виде x^k+1=S(x^k), где S(x)=x-τF(x).
Метод сходится, если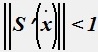
.

№ 34
Итерационный метод Ньютона для решения системы m нелинейных алгебраических уравнений определяется системой уравнений
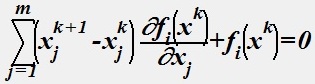, i=1,2,3,...,m
из которой последовательно, начиная с заданного x⁰=(x₁⁰,...,x_m⁰) находятся векторы x^k, k=1,2,...

№ 35
Метод Ньютона имеет квадратичную (наилучшую, наискорейшую, наибыстрейшую, лучшую, хорошую) сходимость, если начальное приближение выбрано достаточно хорошо.
Ответ:

№ 36
Модифицированный метод Ньютона имеет вид F´(x⁰)(x^k+1-x^k)+F(x^k)=0 и обладает линейной сходимостью.

№ 37
Метод Якоби для системы нелинейных алгебраических уравнений состоит в последовательном решении уравнений f_i(x₁^k+,x₂^k+,...,x_i-1^k+,x_i^k+,x_i+1^k+,...,x_m^k+)=0, i=1,2,...,m. В ответ введите шесть цифр, соответствующих верхним индексам после знака “+” переменных x_i^k.
Ответ: (0,0,0,1,0,0)

№ 38
Метод Зейделя для системы нелинейных алгебраических уравнений состоит в последовательном решении уравнений f_i(x₁^k+,x₂^k+,...,x_i^k+,x_i+1^k+,...,x_m^k+)=0. В ответ введите шесть цифр, соответствующих верхним индексам после знака “+” переменных x_i^k.
Ответ: (1,1,1,0,0)

№ 39
Роль ошибок округлений в образовании общей погрешности тем сильнее, чем медленнее сходимость итерационного процесса.

№ 40
Когда внешние итерации осуществляются одним методом, а внутренние итерации - другим получается некоторый новый метод, сочетающий свойства исходных методов, называемый гибридным методом.

Методы решения систем линейных алгебраических уравнений.

№ 41
Выберите метод, отличающийся областью применения.
• Метод Эйткена.

№ 42
Неверное утверждение. Метод LU-разложения предпочтительнее метода Гаусса, так как:
• требует меньшего количества арифметических операций.

№ 43
Неверное утверждение. Метод прогонки находит свое применение при:
• вычислении определенных интегралов.

№ 44
В результате прямого хода (прямой подстановки) метода Гаусса система уравнений приводится к виду
x₁+a₁₂⁽¹⁾x₂+a₁₃⁽¹⁾x₃+...+a_1n⁽¹⁾x_n=a_1,n+1⁽¹⁾
x₂+a₂₃⁽²⁾x₃+...+a_2n⁽²⁾x_n=a_2,n+1⁽²⁾
x₃+...+a_3n⁽³⁾x_n=a_3,n+1⁽³⁾
. . . x_n=a_n,n+1⁽ⁿ⁾.
Для получения решения необходимо провести обратный ход (обратную подстановку).

№ 45
Уравнения

.
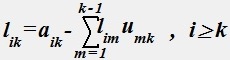
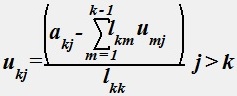описывают алгоритм разложения на треугольные матрицы, называемый алгоритмом Краута, используемом в методе LU-факторизации (разложения).

№ 46
Для решения СЛАУ с трехдиагональной матрицей применяется метод прогонки.

№ 47
Коэффициенты вычисляемые по формулам
.
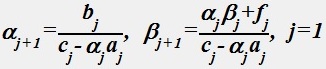α₁=χ₁, β₁=μ₁.
называются прогоночными, а сам процесс их расчета - прямой прогонкой.

№ 48
Процесс рассчета неизвестных по формуле
y_j=α_j+1y_j+1+β_j+1, j=0,1,...,N-1,
.
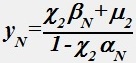называется обратной прогонкой.

№ 49
Количество арифметических операций, выполняемых в ходе метода Гаусса пропорционально третьей степени числа неизвестных уравнений.

№ 50
LU-разложение можно произвести тремя эквивалентыми способами: чередованием строк и столбцов (метод Крамера); разложением по строкам и эквивалентом метода Гаусса.

Интерполяция функций.

№ 51
Преимуществом сплайнов перед обычной интерполяцией является, во-первых, их сходимость и, во-вторых, устойчивость процесса вычислений.

№ 52
В случае, когда интерполируется одна и та же функция f(х), но число узлов интерполяции постепенно увеличивается, удобнее применять:
• формулу Ньютона.

№ 53
Если узлы интерполяции фиксированы и интерполируется не одна, а несколько функций, то удобнее пользоваться:
• формулой Лагранжа.

№ 54
Наибольшее распространение получили:
• кубические сплайны.

№ 55
Точки х_k, расположенные по правилу

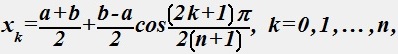
называются Чебышевскими узлами интерполяции, величина отклонения остаточного членa интерполяционного многочлена Лангранжа от нуля при этом оказывается минимальной.

№ 56
Интерполяция состоит в следующем: для данной функции y=f(x) строим многочлен θ(x) степени m, принимающий в заданных точках x_i те же значения y_i, что и функция f(x), т.е. θ(x_i)=y_i, i=0,1,...,n.

№ 57
Интерполяционные многочлены могут строиться как для всего интервала так и отдельно для разных частей рассматриваемого интервала изменения x. В первом случае имеем глобальную, а во втором кусочную (локальную) интерполяцию.

№ 58
Закончите фразу. Как правило, интерполяционные многочлены используются для представления функции в промежуточных точках между крайними узлами интерполяции, т. е. при x₀<x<x_n. Однако иногда они используются и для приближенного вычисления функции вне рассматриваемого отрезка (x<x₀, x>x_n). Это приближение называют экстраполяцией.

№ 59

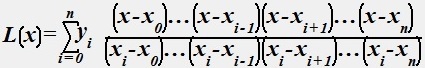
Эта формула называется интерполяционным многочленом Лагранжа.

№ 60

Эта формула называется интерполяционным многочленом Ньютона.

№ 61
Пусть задано 0, 1,..., n соответствий значений функции и аргумента. Степень полинома m при интерполяции:
• =n.

Аппроксимация и сглаживание функций.

№ 62
Отметьте неверное утверждение. Для аппроксимации функций используется:
• многочлен Ньютона.

№ 63
Многочлен, наименее уклоняющийся от нуля называется:
• многочленом Чебышева.

№ 64
Многочлены Чебышева не применяются для:
• сглаживания функций.

№ 65
Корни (нули) многочлена Чебышева расположены в точках
, k=0,1,...,n-1,
а максимумы (минимумы, экстремумы) - в точках
, k=0,1,...,n.

№ 66
Выберите метод, отличающийся областью применения.
• Интерпретация.

№ 67
Если не требуется строгого выполнения условия прохождения функции через все узловые точки, а приоритет отдается простой и компактной записи функции, то для такого приближения используют аппроксимацию - наилучшее приближение функции, заданной таблично.

№ 68
В качестве универсальных функций при аппроксимации используются ортогональные полиномы степени m<n. Введем обобщенный многочлен и будем рассматривать его значения только в узлах x_k, т. е. θ(x_k)=c₀θ₀(x_k)+c₁θ₁(x_k)+...+c_nθ_n(x_k), k=0,1,...,m.
Функции θ_k называются базисными и должны быть ортогональны друг другу.

№ 69
Для вектора погрешностей можно ввести ту или иную норму, например,
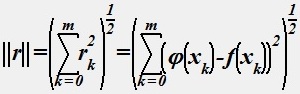(1)
или
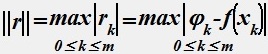(2)
Задача о наилучшем приближении функции f(х) заданной таблично, состоит в нахождении коэффициентов с₀,с₁,...,с_п, исходя из условия минимизации (1) или (2). В зависимости от выбора между (1) или (2) получим различные задачи. Так, (1) соответствует задача о наилучшем среднеквадратичном приближении, а (2) - задача о наилучшем равномерном приближении функции, заданной таблично.

№ 70
Пусть имеется таблица значений {f_i}_i^N=0 функции f(х), полученная, например, путем измерения некоторой физической величины или с помощью численных расчетов. Может оказаться, что f(x) сильно меняется на отдельных участках. В этом случае иногда целесообразно применить процедуру сглаживания (осреднения).
.

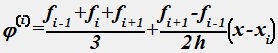№ 71
Пусть задано 0, 1, ...,n соответствий значений функции и аргумента. Степень полинома m при аппроксимации:
• <n.

Численное дифференцирование и интегрирование.

№ 72
Порядок аппроксимации:
Левой разностной производной - 1.
Правой разностной производной - 1.
Центральной разностной производной - 2.

№ 73
Разностные формулы для производных повышенного порядка аппроксимации получают используя:
• многочлен Лагранжа.

№ 74
Разностные формулы для производных повышенного порядка аппроксимации используют значения в пяти узлах.

№ 75
Формула Симпсона основана на замене подынтегральной функции:
• параболой.

№ 76
Погрешность u_x,i-u´(x_i), возникающая при замене дифференциального выражения u´(x_i) разностным выражением u_x,i, называется погрешностью аппроксимации.

№ 77
Выберите метод, отличающийся областью применения.
• Метод дихотомии.

№ 78
Какой порядок точности имеет формула прямоугольников?
• 2.

№ 79
Какой порядок точности имеет формула трапеций?
• 2.

№ 80
Какой порядок точности имеет формула Симпсона?
• 4.

№ 81
Как соотносятся погрешности формулы прямоугольников и формулы трапеций?
• В 2 раза меньше.

№ 82
Сеткой на отрезке [a,b] называется любое конечное множество точек этого отрезка. Функция, определенная в точках сетки называется сеточной функцией. Точки x_i принадлежащие сетке называются узлами. Равномерной сеткой на [a,b] называется множество точек ω_h={x_i=a+ih, i=0,1,...,N}, где h=(b-a)/N - шаг сетки.

Численное решение дифференциальных уравнений.

№ 83
Закончите фразу. Система обыкновенных дифференциальных уравнений du_i(t)|/dt=f_i(t,u₁,u₂,...,u_m), t>0, i=1,2,...,m, дополненная условиями u_i(0)=u_i⁽⁰⁾, i=1,2,...,m называется задачей Коши.

№ 84
Решение дифференциального уравнения по рекуррентной формуле y_n+1=y_n+τf(t_n,y_n), n=0,1,2,..., y₀=u₀ называется методом Эйлера.

№ 85
Фиксируем точку t и построим последовательность сеток ω_τ таких, что τ→0 и t_n=nτ=t. Говорят, что метод y_n+1=y_n+τf(t_n,y_n), n=0,1,2,..., y₀=u₀ сходится в точке t, если |y_n-u(t_n)|→0 при τ→0, t_n=t. Метод сходится на отрезке (0,T], если он сходится в каждой точке t∈(0,T]. Говорят, что метод имеет р-й порядок точности, если существует число р>0 такое, что |y_n-u(t_n)|=O(τ^p) при τ→0.

№ 86
Функция
называется невязкой или погрешностью аппроксимации разностного уравнения .
на решении исходного уравнения

Говорят, что разностный метод аппроксимирует исходное дифференциальное уравнение, если Ψ_n⁽¹⁾→0 при τ→0. Разностный метод имеет р-й порядок аппроксимации, если Ψ_n⁽¹⁾=O(τ^p).

№ 87
Система ОДУ
,
,
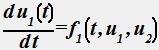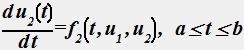дополненная условиями u₁(a)=μ₁, u₂(b)=μ₂, называется граничной (краевой) задачей.

№ 88
Выберите метод, отличающийся областью применения.
• Метод Краута.

№ 89
Какой порядок аппроксимации имеет метод Эйлера?
• 1.

№ 90
Какой порядок аппроксимации имеет симметричная схема?
• 2.

№ 91
Какой порядок аппроксимации имеет метод Рунге Кутта со средней производной?
• 2.

№ 92
Какой порядок аппроксимации имеет метод Рунге Кутта с производной в средней точке?
• 2.

№ 93
Какого максимального порядка аппроксимации используются методы Рунге Кутта?
• 4.

№ 94
Выберите метод, отличающийся областью применения.
• Метод релаксации.

№ 95
Метод стрельбы может использовать:
• методы Рунге Кутта.

№ 96
Решение граничной задачи разностным методом может быть продолжено:
• методом Гаусса.

Уменьшение погрешностей при вычислениях.

№ 97
Формулы Рунге и Эйткена не могут быть применены для:
• метода Гаусса.

№ 98
Апостериорную оценку порядка погрешности метода можно найти по формуле:
• Эйткена.

№ 99
Метод Стеффенсена, имеющий квадратичную сходимость, получается из метода релаксации путем модернизации по алгоритму:
• Эйткена.

№ 100
Что определяется по первой формуле Рунге?
• Главный член погрешности.

№ 101
Что определяется по второй формуле Рунге?
• Уточненное значение искомой величины.

№ 102
Что определяется по формуле Эйткена?
• Апостериорная оценка порядка погрешности метода.

№ 103
Формулы Рунге и Эйткена можно применять к любым сеточным методам, априорную оценку погрешностей которых можно записать через главный член погрешности в виде степенной зависимости от шага.

№ 104
Формулу Эйткена можно использовать для тестирования программ, реализующих вычислительные методы с известной априорной погрешностью.

№ 105
В случае, когда необходимо повысить порядок точности (аппроксимации) применяемого метода более чем на единицу, применяется формула Рунге-Ромберга. Для увеличения этого параметра на 3 необходимо провести расчет с четырьмя значениями шага.

№ 106
Первая формула Рунге позволяет вычислять определенный интеграл с заданной точностью ε>0 путем автоматического выбора переменного шага интегрирования h_i.