Моделирование экономических процессов
для специальности 351400
Мицель А.А.
Кафедра АСУ
Томск-2004

Основные понятия экономико-математического моделирования.

№ 1
Что понимается под экономико-математическими методами?
• Cовокупность экономических и математических научных дисциплин, объединенных для изучения социально-экономических систем и процессов.

№ 2
Задачами экономико-математического моделирования являются:
• aнализ экономических объектов и процессов;
• прогнозирование развития экономических процессов;
• выработка управленческих решений на всех уровнях хозяйственной иерархии.

№ 3
Адекватность модели -
• соответствие модели моделируемому объекту или процессу по существенным для исследования свойствам объекта или процессу.

№ 4
Оптимальное решение -
• наилучшее в каком-то смысле среди допустимых решений.

№ 5
Математическое моделирование включает:
• постановку экономической проблемы и ее качественный анализ;
• построение математической модели и ее анализ;
• подготовка исходной информации;
• численное решение, анализ численных результатов и их применение.

№ 6
По общему целевому назначению экономико-математические модели делятся на:
• теоретико-аналитические и прикладные.

№ 7
По типу подхода к изучаемым социально-экономическим системам модели делятся на:
• дескриптивные и нормативные модели.

№ 8
По конкретному предназначению выделяют:
• балансовые модели;
• трендовые модели;
• оптимизационные и имитационные модели.

Задачи.

№ 9
Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок; при этом используется сырье трех типов: S₁, S₂, S₃.
Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:

Вид сырья	S1	S2	S3
Нормы расхода сырья на 1 пару сапог, усл.ед.	5	2	3
Нормы расхода сырья на 1 пару красовок, усл.ед.	3	1	2
Нормы расхода сырья на 1 пару ботинок, усл.ед.	4	1	2
Расход сырья на один день, усл. ед.	2700	800	1600

Найти ежедневный объем выпуска каждого вида обуви (сапог; кросовок; ботинок).
• 0; 500; 300

№ 10
Предприятие производит продукцию трех видов и использует сырье двух типов. Норма затрат сырья на единицу продукции каждого вида
Стоимость единицы сырья каждого типа задана вектором В=(10,15). Каковы общие затраты предприятия на производство 100 единиц продукции первого вида, 200 единиц продукции второго вида и 150 единиц продукции третьего вида?
• 28000

№ 11
Имеются три банка, каждый из которых начисляет вкладчику определенный годовой процент (свой для каждого банка). Имеется три вкладчика, у каждого по 6000руб. Вкладчики разместили свои деньги в трех банках.
Первый вкладчик 1/3 вклада вложил в банк №1, 1/2 вклада - в банк №2 и оставшуюся часть - в банк №3 и к концу года сумма этих вкладов возросла до 7000 руб.
Второй вкладчик 1/6 вклада положил в банк №1, 2/3 - в банк №2 и 1/6 - в банк №3 , к концу года сумма вкладов составила 6950 руб.
Третий вкладчик 1/2 вклада положил в банк №1, 1/6 - в банк №2 и 1/3 вклада в банк №3, сумма вкладов в конце года составила 7050 руб.
Какой процент выплачивает каждый банк?
• 0,2; 0,15; 0,15

№ 12
Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице:

Тип заготовок	А	Б	В
Способ раскроя №1	3	1	4
Способ раскроя №2	2	6	1
Способ раскроя №3	1	2	5

Найти план выполнения задания.
• 90; 15; 60

Модели производства.

№ 13
Закон убывающей эффективности - это:
• уменьшение прироста производства с ростом объема затрачиваемого ресурса.

№ 14
Производственная функция - это:
• функция, независимая переменная которой принимает значение объемов затраченного ресурса, а зависимая переменная принимает значение объема выпускаемой продукции.

№ 15
Чему равна ПФ при нулевых затратах фактора производства?
• =0.

№ 16
Что показывает изокванта?
• Наборы объемов ресурсов, которые обеспечивают один и тот же объем выпуска продукции.

№ 17
Что показывает предельная производительность?
• На сколько единиц увеличится объем выпуска, если объем затрат одного ресурса увеличится на единицу при неизменном объеме другого ресурса.

№ 18
Что показывает эластичность выпуска по i-му ресурсу?
• На сколько % увеличится объем выпуска, если объем затрат одного ресурса увеличится на 1% при неизменном объеме другого ресурса.

№ 19
Что показывает предельная норма замены i-го ресурса j-ым?
• На сколько единиц нужно увеличить затраты j-го ресурса, при неизменном выпуске, если затраты i-го ресурса уменьшатся на 1.

№ 20
Чему равна эластичность замещения ресурсов для ПФ Солоу?
• 1/(1+ρ).

№ 21
Что показывает функция спроса?
• Обратную зависимость между ценой ресурса и спросом на него.

№ 22
Какие ресурсы называются взаимодополняемыми?
• Частная производная функции спроса на один ресурс по цене на другой меньше 0.

№ 23
Какие ресурсы называются взаимозаменяемыми?
• Частная производная функции спроса на один ресурс по цене на другой больше 0.

№ 24
В статической производственной функции не зависит от времени:
• параметры и значение функции.

№ 25
Укажите производственную функцию Кобба-Дугласа.
• .

№ 26
Дана производственная функция y=f(K,L). Производительность труда, капиталоотдача и капиталовооруженность труда определяются так:
• y/L; y/K; K/L;

№ 27
Дана линейная ПФ y=aK+bL. Производительность труда z и капиталовооруженность труда k связаны соотношением:
• a*k+b.

№ 28
Дана производственная функция y=f(x₁,x₂). Свойство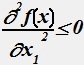
означает:
• c ростом затрат 1-го ресурса при неизменном количестве другого ресурса величина прироста выпуска на каждую дополнительную единицу не растет.

№ 29
Дана производственная функция y=f(x₁,x₂). Свойство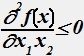
означает:
• при росте одного ресурса предельная эффективность другого ресурса возрастает.

№ 30
Постоянные издержки:
• не зависят от объема производства.

№ 31
Переменные издержки:
• это издержки на единицу продукции.

Задачи.

№ 32
Завод производит пылесосы. Зависимость количества выпускаемых пылесосов от количества задействованных станков имеет вид y=100*K^0.6. Вычислить предельную и среднюю производительность фондов (M,A).
• 60*K^-0.4, 100*K^-0.4.

№ 33
Завод производит пылесосы. Зависимость количества выпускаемых пылесосов от количества задействованных станков имеет вид y=100*K^0.6. Вычислить капиталоемкость, эластичность выпуска по капиталу (K/y;E).
• 0.01*K^0.4, 0.6.

№ 34
Автопредприятие заключило договор с потребителем на перевозки металлообрабатывающих станков от завода изготовителя до потребителя. Зависимость стоимости перевозимых станков от стоимости фондов (стоимости автомобилей + амортизация) имеет вид y=50*K^0.7. Вычислить предельную и среднюю производительность фондов (M,A).
• 35*K^-0.3, 50*K^-0.3.

№ 35
Автопредприятие заключило договор с потребителем на перевозки металлообрабатывающих станков от завода изготовителя до потребителя. Зависимость стоимости перевозимых станков от стоимости фондов (стоимости автомобилей + амортизация) имеет вид y=100*L^0.6. Вычислить трудоемость, эластичность выпуска по труду (L/y;E).
• 0.01*L^0.4, 0.6.

№ 36
Электротехническая компания выпускает светильники. Зависимость выпускаемой продукции в стоимостном исчислении от затрат труда приведена в таблице:

Период	1 - ый месяц	2 - ый месяц	3 - ый месяц	4 - ый месяц	5 - ый месяц
L, y.e.	100	120	130	140	160
y, y.e.	1588.6	1724.5	1787.7	1848.4	1962.8

Найти параметры a,b для производственной функции вида y=a*L^b.
• 200; 0,45

№ 37
Чему равна эластичность однофакторной ЛПФ y=a+b*x?
• <1.

Двухфакторные ПФ.

№ 38
Объем продукции, выпускаемой отраслью, связан с объемом капитала и трудовых ресурсов функцией Y=50*K^0.6*L^0.3, у.д.е. Найти предельную производительность капитала и среднюю производительность труда (M_K, A_L).
• 30*K^-0.4*L^0.3, 50*K^0.6*L^-0.7.

№ 39
Объем продукции, выпускаемой отраслью, связан с объемом капитала и трудовых ресурсов функцией Y=50*K^0.6*L^0.3, у.д.е. Найти предельную производительность труда и среднюю производительность капитала (M_K, A_L).
• 15*K^0.6*L^-0.7, 50*K^-0.4*L^0.3.

№ 40
В таблице приведены значения объема выпуска для различных значений капитала и трудовых ресурсов:

K L	100	200	300	400
10	29.929	36.847	41.613	45.364
20	48.62	59.858	67.600	73.694
30	64.577	79.503	89.787	97.880
40	78.983	97.239	109.817	119.716

Найти параметры a, α, β для производственной функции вида y=a*K^α*L^β.
• 1,5; 0,3; 0,7

№ 41
Найти R_L,K для ПФКД y=a*K^α*L^β. Использовать формулу: R_ij=-dx_j / dx_i
• β/α*K/L.

№ 42
Найти E_L, E_K для ПФКД.
• E_L<1; E_K<1.

№ 43
Найти R_K,L для ПФКД y=a*K^α*L^β. Использовать формулу: R_ij=-dx_j / dx_i
• α/β*L/K.

№ 44
Для ЛПФ вычислить эластичность замещения труда капиталом E_L,K.
• →∞.

Балансовые модели.

№ 45
Суть балансового метода исследования социально-экономических систем:
• метод взаимного сопоставления имеющихся материальных, трудовых и финансовых ресурсов и потребностей в них.

№ 46
Какой принцип лежит в основе схемы межотраслевого статического баланса?
• Разделение совокупного продукта на две части: промежуточный и конечный продукт.

№ 47
Что содержится в 1-ом квадранте МОБ?
• Межотраслевые потоки продукции.

№ 48
Что содержится в 2-ом квадранте МОБ?
• Конечный продукт всех отраслей материального производства.

№ 49
Что содержится в 3-ем квадранте МОБ?
• Национальный доход со стороны его стоимостного состава.

№ 50
Что содержится в 4-ом квадранте МОБ?
• Конечное распределение и использование национального дохода.

№ 51
Как вычисляются коэффициенты прямых материальных затрат - a_ij?
• x_ij / X_j.

№ 52
Что показывают коэффициенты прямых материальных затрат - a_ij?
• Какое количество продукции i-ой отрасли необходимо, если учитывать только прямые затраты, для производства единицы продукции в j-ой отрасли.

№ 53
Как вычисляется матрица коэффициентов полных материальных затрат - B?
• (E-A)^-1.

№ 54
Что показывают коэффициенты полных материальных затрат?
• Показывает, какое количество продукции i- й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j -й отрасли.

№ 55
Матрица А называется продуктивной, если существует X≥0 , такое что:
• X > A*X.

№ 56
Необходимое и достаточное условие продуктивности матрицы А:
• выполнение одного из условий продуктивности.

№ 57
Основное балансовое равенство в межотраслевом балансе труда:
• t*X=T*Y.

№ 58
Экономический смысл коэффициентов прямой трудоемкости:
• затраты живого труда на единицу продукции отрасли.

№ 59
Экономический смысл коэффициентов полной трудоемкости:
• совокупные затраты живого труда и затраты овеществленного труда, перенесенные на продукт через израсходованные средства производства.

№ 60
Основное балансовое равенство в межотраслевом балансе фондов:
• f*X=F*Y.

№ 61
Экономический смысл коэффициентов прямой фондоемкости:
• затраты фондов непосредственно занятых в производстве данной отрасли, в расчете на единицу ее валовой продукциию.

№ 62
Экономический смысл коэффициентов полной фондоемкости:
• объем фондов, необходимых во всех отраслях для выпуска единицы конечной продукции j-ой отрасли.

№ 63
Основное отличие статической модели межотраслевого баланса от динамической.
• в динамической модели производственные капитальные вложения выделяются из состава конечной продукции и включается учет фактора времени.

Задачи.

№ 64
Имеется три отрасли: промышленность, сельское хозяйство и прочие отрасли. Дана матрица прямых затрат и вектор конечной продукции в у.е. Найти плановый объем валовой продукции.

• (102,197; 41,047; 26,383)

№ 65
В таблице приведены коэффициенты прямых материальных затрат, объемы конечной продукции, объемы фондов по отраслям в межотраслевом балансе для трех отраслей:

Производящие отрасли	1	2	3	Ф
Коэффициент прямых затрат-1	0.2	0.5	0.2	400
Коэффициент прямых затрат-2	0.2	0.3	0.2	500
Коэффициент прямых затрат-3	0.1	0.2	0.4	300
Конечная продукция	50	0	30

Рассчитать коэффициенты прямой и полной фондоемкости. Ответ введите в виде последовательности чисел: сначала коэффициенты прямой фондоемкости, затем коэффициенты полной фондоемкости.
• 3,803; 4,549; 2,465; 11,1; 18,411; 13,945

№ 66
Два цеха выпускают продукцию двух видов: первый цех продукцию первого вида, второй цех продукцию второго вида. Часть выпускаемой продукции идет на внутреннее потребление, остальная является конечным продуктом.

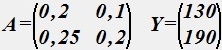
Проверить продуктивность матрицы.
• Продуктивна.

№ 67
В таблице приведены потоки материальных затрат, объемы конечной и валовой продукции в у.е для двух отраслей:

Отрасли производители	Отрасли потребители
	Текущее материальное потребление		Конечная продукция	Валовая продукция
	1	2
1	65	30	40	130
2	25	40	90	155

Рассчитать матрицу прямых и полных материальных затрат. Ответ введите в виде последовательности чисел - сначала для матрицы прямых материальных затрат (построчно), затем для матрицы полных материальных затрат.
• 0,5; 0,194; 0,192; 0,258; 2,223; 0,581; 0,575; 1,498

№ 68
На основании данных, приведенных в таблице, рассчитать коэффициенты прямой и полной трудоемкости:

Производящие отрасли	1	2	3	L
Коэффициент прямых затрат-1	0.2	0.5	0.2	100
Коэффициент прямых затрат-2	0.2	0.3	0.2	300
Коэффициент прямых затрат-3	0.1	0.2	0.4	250
Конечная продукция	50	0	30

Ответ введите в виде последовательности чисел: сначала коэффициенты прямой трудоемкости, затем коэффициенты полной трудоемкости.
• 0,951; 2,73; 2,054; 4,573; 9,483; 8,109

Линейное программирование.

№ 69
Сформулируйте задачу планирования производства.
• Для изготовления нескольких видов продукции используют различные виды ресурсов. Нужно составить план производства, при котором прибыль максимальна.

№ 70
Сформулируйте задачу составления рациона.
• Имеется несколько видов корма, содержащих питательные вещества (например, S1,S2,S3). Составить дневной рацион, имеющий минимальную стоимость, а содержание питательных веществ не менее установленного предела.

№ 71
Сформулируйте задачу о загрузке оборудования.
• Предприятию задан план производства продукции по времени и номенклатуре. Составить план работы станков (максимально распределить выпуск продукции между станками), чтобы затраты на производство были минимальны.

№ 72
Сформулируйте задачу о раскрое материалов.
• Составить план раскроя материала (раскрой может быть произведен различными способами), который обеспечивает максимальное число комплектов.

№ 73
Сформулируйте задачу технического контроля.
• На фирме существует отдел технического контроля, на котором работают контролеры различных разрядов. Определить оптимальный состав Отдела технического контроля, при котором общие затраты на контроллеров минимальны.

№ 74
Где расположено оптимальное решение на допустимой области?
• На одной из вершин допустимой области.

№ 75
Стандартная форма записи задач линейного программирования:
• min f(x)=C^Tx
Ax=b, b>0;
x≥0.

№ 76
Что называют допустимым решением?
• Вектор Х, удовлетворяющий всем ограничениям ЗЛП.

№ 77
Допустимая область - это:
• множество всех допустимых решений.

№ 78
В каком случае ЗЛП называется противоречивой?
• Если допустимая область равна нулю.

№ 79
Какой план называют оптимальным?
• План Х*, для которого целевая функция достигает минимума или максимума.

№ 80
Сформулируйте двойственную задачу ЛП.
• Определить такой набор цен ресурсов, при котором общие затраты на ресурсы минимальны (при условии, что затраты на ресурсы при производстве каждого вила продукции будут не менее цены этой продукции).

№ 81
Основное неравенство теории двойственности:
•.

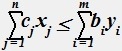№ 82
Экономический смысл Первой теоремы двойственности:
• план производства и набор оценок ресурсов оказывается оптимальным только тогда, когда прибыль от произведенной продукции при внешних ценах равна затратам на ресурсы по внутренним ценам.

№ 83
Сформулируйте Вторую теорему двойственности.
• Компоненты оптимального решения двойственной задачи равен значениям частных производных целевой функции.

№ 84
Сформулируйте четвертую теорему двойственности.
• Компоненты оптимального решения двойственной задачи равны по абсолютной величине коэффициентам при соответствующих переменных целевой функции прямой задачи, записанной для оптимального плана.
• Компоненты оптимального решения прямой задачи равны по абсолютной величине коэффициентам при соответствующих переменных целевой функции двойственной задачи, записанной для оптимального плана.

№ 85
Объективно обусловленные оценки - это:
• компоненты оптимального решения двойственной задачи.

№ 86
Укажите особенности экономико-математической модели транспортной задачи:
• система ограничений есть система уравнений;
• коэффициенты при переменных системы ограничений равны единице или нулю;
• каждая переменная входит в систему ограничений два раза 4.

№ 87
Сформулируйте транспортную задачу.
• Составить такой план перевозок для каждой пары “поставщик - потребитель” так, чтобы мощности всех поставщиков были реализованы, спросы всех потребителей были удовлетворены, суммарные затраты на перевозку были бы минимальны.

№ 88
В открытой модели транспортной задачи:
• ограничения заданы в виде неравенств.

№ 89
Назовите один из методов нахождения первоначального базисного распределения поставок?
• Метод “северо-западного” угла.

№ 90
Сформулируйте критерий оптимальности базисного распределения поставок.
• Базисное распределение поставок оптимально тогда и только тогда, когда оценки всех свободных клеток неотрицательны.

№ 91
Решение транспортной задачи, в оптимальном плане перевозок которой есть нулевые оценки свободных клеток, называется:
• неединственным.

№ 92
Эквивалентность между элементами производственной и транспортной системы устанавливается следующим образом:
• в транспортной системе предложение в пункте I соответствует объему производства в период I в производственной системе;
• спрос в пункте j в транспортной системе соответствует реализации в период j в производственной системе;
• стоимость перевозки из пункта I в пункт j в транспортной системе соответствует стоимости производства и хранения за период от I до j в производственной системе.

№ 93
Основное отличие метода наименьших стоимостей от метода “северо-западного” угла заключается в следующем:
• в методе наименьших стоимостей учитываются транспортные расходы.

№ 94
Что называется потенциалом данной строки (столбца)?
• Число, которое прибавляется к коэффициентам затрат выделенной строки (столбца).

№ 95
Понятие целочисленного программирования.
• Раздел математического программирования, изучающий экстремальные задачи, в которых на искомые переменные накладывается условие целочисленности.

№ 96
Как называется метод решения задач целочисленного программирования?
• Метод Гомори.

№ 97
Сформулируйте задачу о назначениях.
• Имеется n работников, которые могут выполнить n работ. Известен доход, который приносит i-ый работник при выполнении j-ой работы. Требуется поручить каждому из работников выполнение одной работы, чтобы максимизировать суммарный доход.

№ 98
Укажите метод решения задач многокритериальной оптимизации:
• оптимизация одного, признанного наиболее важным критерия, остальные критерии играют роль дополнительных ограничений;
• упорядочение заданного множества критериев и последовательная оптимизация по каждому из них;
• сведение многих критериев к одному путем введения экспертных весовых коэффициентов для каждого их критериев.

№ 99
В чем суть критерия оптимальности Парето?
• Суть в улучшении одних показателей при условии, чтобы другие не ухудшались.

№ 100
Что называют областью Парето?
• Множество допустимых решений, для которых невозможно одновременное улучшение всех частных показателей эффективности.

Задачи по линейному программированию.

№ 101
Для изготовления сплава из меди, олова и цинка в качестве сырья используют два сплава тех же металлов, отличающиеся составом и стоимостью. Данные от этих сплавах приведены в таблице:

Компоненты сплава	Содержание компонентов в %
	сплав № 1	сплав № 2
Медь	10	10
Олово	10	30
Цинк	80	60
Стоимость 1 кг	4	6

Получаемый сплав должен содержать не более 2 кг меди, не менее 3 кг олова, а содержание цинка может составлять от 7,2 до 12,8 кг. Определить количества Xj, j=1,2, сплавов каждого вида, обеспечивающие получение нового сплава с минимальными затратами на сырье. Составить математическую модель задачи и решить задачу. Ответ введите в виде последовательности чисел через пробел для количества сплава Xj, j=1, 2.
• 2; 9,333

№ 102
Для изготовления сплава из меди, олова и цинка в качестве сырья используют два сплава тех же металлов, отличающиеся составом и стоимостью. Данные от этих сплавах приведены в таблице:

Компоненты сплава	Содержание компонентов в %
	сплав № 1	сплав № 2
Медь	10	10
Олово	10	30
Цинк	80	60
Стоимость 1 кг	4	6

Получаемый сплав должен содержать не более 2 кг меди, не менее 3 кг олова, а содержание цинка может составлять от 7,2 до 12,8 кг. Определить количества Xj, j=1,2, сплавов каждого вида, обеспечивающие получение нового сплава с минимальными затратами на сырье. Сформулировать двойственную задачу и решить ее. Ответ введите в виде последовательности чисел через пробел для переменных двойственной задачи.
• 0; 13,333; 3,333; 0

№ 103
Для изготовления двух видов изделий А1 и А2 завод использует в качестве сырья алюминий и медь. На изготовлении изделий заняты токарные и фрезерные станки. Исходные данные задачи приведены в таблице:

Виды ресурсов	Аллюминий, кг	Медь, кг	Токарные станки, станко-час	Фрезерные станки, станко-час	Прибыль на 1 изделие, тыс.руб
Объем ресурсов	570	420	5600	3400
Нормы расхода на 1 изделие А1	10	20	300	200	3
Нормы расхода на 1 изделие А2	70	50	400	100	8

Определить количество Xj, j=1,2 изделий Aj, которые необходимо изготовить для достижения максимальной прибыли. Составить математическую модель задачи и решить задачу. Ответ введите в виде последовательности чисел через пробел для количества изделий Xj, j=1,2.
• 1; 8

№ 104
Для изготовления двух видов изделий А1 и А2 завод использует в качестве сырья алюминий и медь. На изготовлении изделий заняты токарные и фрезерные станки. Исходные данные задачи приведены в таблице:

Виды ресурсов	Аллюминий, кг	Медь, кг	Токарные станки, станко-час	Фрезерные станки, станко-час	Прибыль на 1 изделие, тыс.руб
Объем ресурсов	570	420	5600	3400
Нормы расхода на 1 изделие А1	10	20	300	200	3
Нормы расхода на 1 изделие А2	70	50	400	100	8

Определить количество Xj, j=1,2 изделий Aj, которые необходимо изготовить для достижения максимальной прибыли. Сформулировать двойственную задачу и решить ее. Ответ введите в виде последовательности чисел через пробел для переменных двойственной задачи.
• 0,011; 0,144; 0; 0

№ 105
Из одного города в другой ежедневно отправляются пассажирские и скорые поезда. В таблице 3 указаны: состав поезда каждого типа, количество имеющихся в парке вагонов различных видов для формирования поездов и максимальное число пассажиров, на которое рассчитан вагон каждого вида.

Поезда	Скорый	Пассажирский	Число пассажиров	Парк вагонов
Багажный	1	1	-	12
Почтовый	1	-	-	8
Плацкартный	5	8	58	81
Купейный	6	4	40	70
Мягкий	3	1	32	26

Определить число скорых x1 и пассажирских x2 поездов, которые необходимо формировать ежедневно из имеющегося парка вагонов, чтобы число перевозимых пассажиров было максимальным. Составить математическую модель задачи и решить задачу. Ответ введите в виде последовательности чисел через пробел для количества скорых и пассажирских поездов.
• 5; 7

№ 106
Из одного города в другой ежедневно отправляются пассажирские и скорые поезда. В таблице 3 указаны: состав поезда каждого типа, количество имеющихся в парке вагонов различных видов для формирования поездов и максимальное число пассажиров, на которое рассчитан вагон каждого вида.

Поезда	Скорый	Пассажирский	Число пассажиров	Парк вагонов
Багажный	1	1	-	12
Почтовый	1	-	-	8
Плацкартный	5	8	58	81
Купейный	6	4	40	70
Мягкий	3	1	32	26

Определить число скорых x1 и пассажирских x2 поездов, которые необходимо формировать ежедневно из имеющегося парка вагонов, чтобы число перевозимых пассажиров было максимальным. Сформулировать двойственную задачу и решить ее. Ответ введите в виде последовательности чисел через пробел для переменных двойственной задачи.
• 10; 0; 0; 576; 0

№ 107
Завод производит продукцию двух видов A1 и А2, используя сырье, запас которого составляет 16 т. Согласно плану выпуск продукции А1 должен составлять не менее 60% общего объема выпуска. Расход сырья на изготовление 1 т продукции А1 и А2 составляет соответственно 0.05 и 0.1 т. Стоимость 1 т продукции А1 и А2 составляет соответственно 900 руб. и 500 руб. Определить план выпуска продукции А1 и А2, при котором стоимость выпущенной продукции будет максимальной. Составить математическую модель задачи и решить задачу. Ответ введите в виде последовательности чисел для количества продукции А1 и А2.
• 320; 0

№ 108
Завод производит продукцию двух видов A1 и А2, используя сырье, запас которого составляет 16 т. Согласно плану выпуск продукции А1 должен составлять не менее 60% общего объема выпуска. Расход сырья на изготовление 1 т продукции А1 и А2 составляет соответственно 0.05 и 0.1 т. Стоимость 1 т продукции А1 и А2 составляет соответственно 900 руб. и 500 руб. Определить план выпуска продукции А1 и А2, при котором стоимость выпущенной продукции будет максимальной. Сформулировать двойственную задачу и решить ее. Ответ введите в виде последовательности чисел через пробел для переменных двойственной задачи.
• 18000; 0

№ 109
Процесс изготовления изделий двух видов Р1 и Р2 состоит в последовательной обработке каждого из них на трех станках. Время использования i-го станка составляет b_i часов в сутки (i=1,2,3). Время обработки каждого изделия j-го вида (j=1,2) на i-м станке равно a_ij часам. Прибыль от реализации одного изделия j-го вида составляет c_j руб. Составить план суточного выпуска изделий так, чтобы прибыль от их производства была максимальной для следующих исходных данных:

Обрабатывающие станки	Время работы станков bi, час	Время обработки изделий, aij, час
		Р1	Р2
1	10	3,5	1,2
2	15	2,4	3,8
3	18	0,5	1,0
Стоимость единицы продукции, cj, руб		400	750

Составить математическую модель задачи и решить задачу. Ответ введите в виде последовательности чисел для количества изделий Р1 и Р2.
• 0; 3,947

№ 110
Процесс изготовления изделий двух видов Р1 и Р2 состоит в последовательной обработке каждого из них на трех станках. Время использования i-го станка составляет b_i часов в сутки (i=1,2,3). Время обработки каждого изделия j-го вида (j=1,2) на i-м станке равно a_ij часам. Прибыль от реализации одного изделия j-го вида составляет c_j руб. Составить план суточного выпуска изделий так, чтобы прибыль от их производства была максимальной для следующих исходных данных:

Обрабатывающие станки	Время работы станков bi, час	Время обработки изделий, aij, час
		Р1	Р2
1	10	3,5	1,2
2	15	2,4	3,8
3	18	0,5	1,0
Стоимость единицы продукции, cj, руб		400	750

Сформулировать двойственную задачу и решить ее. Ответ введите в виде последовательности чисел для переменных двойственной задачи.
• 0; 197,368; 0

№ 111
Предприятие, располагающее ресурсами сырья трех видов Bi (i=1,2,3,4) может производить продукцию четырех видов Aj (j=1,2,3,4). В таблице указаны затраты ресурсов Bi на изготовление 1 т продукции Aj, объем ресурсов и прибыль, получаемая от изготовления 1 т продукции Aj.

Вид сырья	Вид продукции
	А1	А2	А3	А4	Объем ресурсов
В1	4	5	2	3	60
В2	30	14	18	22	400
В3	16	14	8	10	138
Прибыль, руб.	48	25	56	30

Определить ассортимент выпускаемой продукции, при котором полученная прибыль будет максимальной и при условии что продукции A2 необходимо выпустить не менее 8 т, продукции A4 - не более 5 т, а продукции A1 и A3 - в отношении 2:1. Составить математическую модель задачи и решить задачу. Ответ введите в виде последовательности чисел для количества изделий Aj (j=1,2,3,4).
• 1,3; 8; 0,65; 0

№ 112
Предприятие, располагающее ресурсами сырья трех видов Bi (i=1,2,3,4) может производить продукцию четырех видов Aj (j=1,2,3,4). В таблице указаны затраты ресурсов Bi на изготовление 1 т продукции Aj, объем ресурсов и прибыль, получаемая от изготовления 1 т продукции Aj.

Вид сырья	Вид продукции
	А1	А2	А3	А4	Объем ресурсов
В1	4	5	2	3	60
В2	30	14	18	22	400
В3	16	14	8	10	138
Прибыль, руб.	48	25	56	30

Определить ассортимент выпускаемой продукции, при котором полученная прибыль будет максимальной и при условии, что продукции A2 необходимо выпустить не менее 8 т, продукции A4 - не более 5 т, а продукции A1 и A3 - в отношении 2:1. Сформулировать двойственную задачу и решить ее. Ответ введите в виде последовательности чисел для переменных двойственной задачи.
• 0; 0; 3,8; 28,2; 0; 12,8

№ 113
Предприятие, располагающее ресурсами сырья трех видов Bi (i=1,2,3,4) может производить продукцию четырех видов Aj (j=1,2,3,4). В таблице указаны затраты ресурсов Bi на изготовление 1 т продукции Aj, объем ресурсов и прибыль, получаемая от изготовления 1 т продукции Aj.

Вид сырья	Вид продукции
	А1	А2	А3	А4	Объем ресурсов
В1	7	9	1	3	65
В2	35	24	38	23	450
В3	18	16	66	35	150
Прибыль, руб.	74	36	66	35

Определить ассортимент выпускаемой продукции, при котором полученная прибыль будет максимальной и при условии что производственные издержки на 1 т продукции Aj, (j=1,2,3,4) составляют соответственно 3, 9, 12 и 6 руб., а суммарные издержки не должны превышать 96 руб. Составить математическую модель задачи и решить задачу. Ответ введите в виде последовательности чисел для количества изделий Aj (j=1,2,3,4).
• 8,333; 0; 0; 0

№ 114
Предприятие, располагающее ресурсами сырья трех видов Bi (i=1,2,3,4) может производить продукцию четырех видов Aj (j=1,2,3,4). В таблице указаны затраты ресурсов Bi на изготовление 1 т продукции Aj, объем ресурсов и прибыль, получаемая от изготовления 1 т продукции Aj.

Вид сырья	Вид продукции
	А1	А2	А3	А4	Объем ресурсов
В1	7	9	1	3	65
В2	35	24	38	23	450
В3	18	16	66	35	150
Прибыль, руб.	74	36	66	35

Определить ассортимент выпускаемой продукции, при котором полученная прибыль будет максимальной и при условии что производственные издержки на 1 т продукции Aj, (j=1,2,3,4) составляют соответственно 3, 9, 12 и 6 руб., а суммарные издержки не должны превышать 96 руб. Сформулировать двойственную задачу и решить ее. Ответ введите в виде последовательности чисел для переменных двойственной задачи.
• 0; 0; 4,111; 0

№ 115
Завод получает 4 вида полуфабрикатов Bi в количествах: B1- 400 т, B2 - 250 т, B3 -350 т и B4 -100 т. В результате смешения этих компонентов получают 3 вида продукции Aj. Пропорции смешиваемых полуфабрикатов следующие: для A1- 2:3:5:2, для A2 - 3:1:2:1, для A3 - 2:2:1:3. Стоимость 1 т продукции Aj составляет: A1 - 12 руб., A2 -10 руб., A3-15 руб. Составить оптимальный план выпуска продукции по критерию максимальной стоимости выпущенной продукции. Составить математическую модель задачи и решить задачу. Ответ введите в виде последовательности чисел для количества продукции Aj (j=1,2,3).
• 0; 0; 600

№ 116
Завод получает 4 вида полуфабрикатов Bi в количествах: B1- 400 т, B2 - 250 т, B3 -350 т и B4 -100 т. В результате смешения этих компонентов получают 3 вида продукции Aj. Пропорции смешиваемых полуфабрикатов следующие: для A1- 2:3:5:2, для A2 - 3:1:2:1, для A3 - 2:2:1:3. Стоимость 1 т продукции Aj составляет: A1 - 12 руб., A2 -10 руб., A3-15 руб. Составить оптимальный план выпуска продукции по критерию максимальной стоимости выпущенной продукции. Сформулировать двойственную задачу и решить ее. Ответ введите в виде последовательности чисел для переменных двойственной задачи.
• 0; 0; 0; 72

№ 117
Завод получает 4 вида полуфабрикатов Bi в количествах: B1 - 450 т, B2 - 200 т, B3 - 300 т и B4 - 150 т. В результате смешения этих компонентов получают 3 вида продукции Aj. Пропорции смешиваемых полуфабрикатов следующие: для A1 - 2:4:5:3, для A2 - 2:1:1:2, для A3 - 1:2:4:3. Составить оптимальный план выпуска продукции по критерию максимального использования полуфабрикатов. Составить математическую модель задачи и решить задачу. Ответ введите в виде последовательности чисел для количества продукции Aj (j=1,2,3).
• 0; 0; 700

№ 118
Завод получает 4 вида полуфабрикатов Bi в количествах: B1 - 450 т, B2 - 200 т, B3 - 300 т и B4 - 150 т. В результате смешения этих компонентов получают 3 вида продукции Aj. Пропорции смешиваемых полуфабрикатов следующие: для A1 - 2:4:5:3, для A2 - 2:1:1:2, для A3 - 1:2:4:3. Составить оптимальный план выпуска продукции по критерию максимального использования полуфабрикатов. Сформулировать двойственную задачу и решить ее. Ответ введите в виде последовательности чисел для переменных двойственной задачи.
• 0; 1,4; 0; 2,8