
Моделирование систем
для специальности 210100
Решетникова Г.Н.
Кафедра КСУП
Томск-2004
№ 1
Что характеризует качественные различия модели и оригинала?
• Упрощенность модели.
№ 2
Что характеризует количественные различия между моделью и оригиналом?
• Приближенность модели.
№ 3
Модель “черного ящика” отражает следующие свойства системы:
• целостность;
• обособленность от среды.
№ 4
Модель состава системы описывает:
• элементы и подсистемы, из которых состоит система.
№ 5
Системой называется:
• совокупность взаимосвязанных элементов, обособленная от среды и взаимодействующая с ней как целое.
№ 6
Системы, моделирование которых затруднительно вследствие недостатка информации для управления, называются:
• сложными.
№ 1
Математическое моделирование - это:
• метод исследования реальных явлений или процессов путем построения их математических моделей и исследования этих моделей.
№ 2
Решая прямую задачу при построении математической модели, получают:
• выходные данные модели.
№ 3
Решая обратную задачу при построении математической модели, получают:
• характеристики модели.
№ 4
Укажите независимые переменные:
• переменные, характеризующие состояние системы;
• входные воздействия;
• воздействия внешней среды.
№ 5
Укажите зависимые переменные:
• выходные характеристики;
• показатели эффективности.
№ 6
Если математическая модель не содержит случайных элементов, то имеем:
• детерминированную модель.
№ 7
Если математическая модель содержит случайные элементы, то имеем:
• вероятностную модель.
№ 1
Статистическое моделирование - это:
• вид компьютерного моделирования, позволяющий получать статистические данные о процессах в моделируемой системе.
№ 2
Совокупность приемов, позволяющих получать решения математических или физических задач при помощи случайных многократных испытаний - это:
• метод Монте-Карло.
№ 1
Суть методов Монте-Карло заключается в том, что для вычисления интеграла I строится последовательность I1I2,... для которой справедливо:
• ![]() .
.
№ 2
Оценка дисперсии случайной величины #mathksi может быть вычислена по формуле:
• 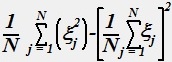 .
.
№ 3
Погрешность простейшего метода Монте-Карло приблизительна равна:
• 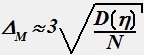 .
.
№ 4
Вычисление однократного интеграла на интервале [0,1] простейшим методом Монте-Карло осуществляется следующим образом:
• ![]() .
.
№ 5
Вычисление однократного интеграла на интервале [0,1] геометрическим методом Монте-Карло осуществляется следующим образом:
• I=V/N.
№ 6
Погрешность геометрического метода Монте-Карло приблизительна равна:
• 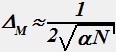 .
.
№ 1
Имитационная модель - это:
• программы и алгоритмы, позволяющие имитировать на ЭВМ поведение отдельных элементов системы и связей между ними в течение заданного времени моделирования.
№ 2
Все имитационные модели функционируют как модели:
• типа черного ящика.
№ 3
Два типа целей имитационного моделирования.
• Приобретение.
• Сохранение.
№ 4
Чтобы обеспечить имитацию параллельных событий системы, в имитационной модели используют:
• системное модельное время.
№ 5
Принцип ‘Δt’ заключается в изменении:
• модельного времени с фиксированным шагом.
№ 6
Принцип ‘Δx’ заключается в изменении:
• модельного времени в моменты наступления событий.
№ 7
Способ имитации системы - это способ:
• формирования фазовой траектории системы.
№ 8
Укажите способы имитации:
• способ, основанный на просмотре активностей;
• процессный.
№ 9
На первом этапе имитационного моделирования проводится:
• построение математической модели.
№ 10
На втором этапе имитационного моделирования проводится:
• разработка моделирующего алгоритма и построение имитационной модели.
№ 11
На третьем этапе имитационного моделирования проводится:
• исследование исходной системы с помощью имитационной модели.
№ 12
В результате имитационного моделирования системы при заданных значениях вектора параметров fi1´∈FI1 и интервала [0,T] получают:
• фазовую траекторию системы;
• значения показателей эффективности.
№ 1
Агрегативное моделирование - это:
• представление сложной системы в виде конечного числа взаимосвязанных элементов, допускающих стандартное математическое описание.
№ 2
А - модель в момент времени t*∈[t0,T] находится в особом состоянии, если t* - момент:
• поступления воздействия внешней среды;
• выдачи выходного сигнала;
• поступления управляющего сигнала.
№ 3
Область в пространстве, при попадании фазовой траектории агрегата в которую выдается выходной сигнал, называется:
• критической областью.
№ 4
Множество всех возможных состояний агрегата разделяется на подмножества:
• особых состояний;
• неособых состояний.
№ 5
Агрегат - это:
• абстрактное математическое описание моделей различного типа.
№ 1
Интеграл I=∫abf(x)dx вычисляется по квадратурной формуле правых прямоугольников:
• ![]() .
.
№ 2
Задача Коши для обыкновенного дифференциального уравнения y´=f(x,y(x)), y(x0)=y0 решается методом Адамса:
• yi+1 = yi + h/24 [ 55f(xi,yi)-59f(xi-1,yi-1)+37f(xi-2,yi-2)-9f(xi-3,yi-3) ].
№ 1
Интерполяционная формула Ньютона:
• Pn(x)=f(x0)+(x-x0)f(x0,x1)+(x-x0)(x-x1)f(x0,x1,x2)+(x-x0)(x-x1)+...+(x-xn-1)f(x0,x1,...,xn).
№ 2
Интерполяционная формула Лагранжа:
• 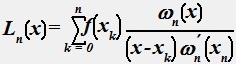 .
.
№ 3
Решение нелинейного уравнения f(x)=0 методом Ньютона осуществляется по итерационной формуле:
• 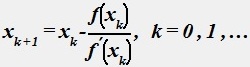 .
.
№ 4
Решение нелинейного уравнения f(x)=0 методом простых итераций осуществляется по итерационной формуле:
• xk+1=θ(xk), k=0,1,...
№ 5
Метод Лобачевского нахождения корней полинома основан на соотношениях:
• Виетта.
№ 6
Какая система линейных алгебраических уравнений называется хорошо обусловленной?
• Eсли малым погрешностям исходных данных соответствуют малые погрешности в решении.
№ 7
Какая система линейных алгебраических уравнений называется плохо обусловленной?
• Eсли малым погрешностям исходных данных соответствуют большие погрешности в решении.
№ 5
Абсолютная погрешность функции y=f(x1,x2,..,xn) относительно соответствующих погрешностей аргументов вычисляется по формуле:
• ![]() .
.
№ 6
Относительная погрешность функции y=f(x1,x2,..,xn) относительно соответствующих погрешностей аргументов вычисляется по формуле:
• 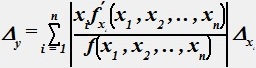 .
.
№ 12
Для того чтобы погрешность интерполирования была наименьшей, необходимо в качестве узлов интерполирования брать корни многочлена:
• Чебышева.
№ 7
Исходя из каких условий строятся коэффициенты параболического сплайна?
• Совпадение значений функции и сплайна в узловых точках.
• Непрерывность первой производной сплайна.
• Непрерывность сплайна.
№ 8
Как вычисляется кубическая норма вектора x=(x1,x2,..xn)T?
• ||x||=max|xi|.
№ 9
Как вычисляется кубическая норма матрицы A=(aij), i,j=1,n ?
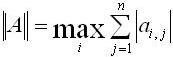
№ 10
При решении краевой задачи для обыкновенного дифференциального уравнения методом сеток функция решения ищется в виде:
• y(x0),y(x1),..y(xn).
№ 11
ППри решении краевой задачи для обыкновенного дифференциального уравнения методом коллокации функция решения ищется в виде:
• ![]() .
.
№ 1
Модель объекта управления x°(t)=f(x(t),u(t)) является:
• непрерывной;
• нелинейной;
• стационарной;
• детерминированной.
№ 2
Система управления называется адаптивной, если:
• объем априорной информации об объекте достаточен для достижения цели управления.
№ 3
Переменные состояния описывают:
• поведение системы в будущем
| на главную | база по специальностям | база по дисциплинам | статьи |
Другие статьи по теме
