
Моделирование систем - 2
для специальности 220200
Шевченко Н.Ю.
Кафедра АОИ
Томск-2003
№ 1
Сколько игроков принимают участие в антагонистической игре?
• (2)
№ 2
При каких условиях игра называется бесконечной?
• хотя бы у одного игрока бесконечное множество стратегий.
№ 3
Игра, в которой целью каждого игрока является максимизация индивидуального выигрыша без возможностей объединения игроков, называется:
• некооперативной.
№ 4
Игра, в которой интересы игроков прямо противоположны, называется:
• антагонистической.
№ 5
Стратегия игрока – это:
• правило поведения игрока от начала до конца игры.
№ 6
В математическую модель игры не входит:
• цена игры.
№ 7
Конечной целью исследования игры является:
• нахождение оптимальных стратегий для каждого из игроков.
№ 8
Сколько игроков может принимать участие в кооперативной игре?
• любое количество больше одного.
№ 9
При нахождении решения игры прежде всего учитываются предпочтения:
• все игроки равны.
№ 10
Существуют ли общие принципы оптимальности для всех игр?
• нет, для каждого класса игр выбираются свои принципы оптимальности.
Игра имеет решение в чистых стратегиях.
Найти цену игры.
№ 11
| 3 | 5 | 2 | 1 |
| 2 | 2 | 2 | 2 |
| 4 | 4 | 5 | 3 |
| 1 | 3 | 5 | 2 |
№ 12
| -2 | 4 | -3 | 1 |
| 5 | 0 | 0 | 2 |
| 3 | 2 | -1 | 6 |
| 4 | 6 | 0 | -2 |
№ 14
| 2 | 1 | 3 | 5 |
| 4 | 5 | 6 | 4 |
| 6 | 8 | 6 | 6 |
| 2 | 1 | 1 | 1 |
№ 16
| -5 | 6 | 2 | 3 |
| 4 | -2 | 6 | 0 |
| 2 | 3 | 9 | 1 |
| 4 | 5 | 4 | 5 |
№ 23
| 3 | 4 | 4 | 3 |
| -2 | 5 | 2 | 6 |
| 3 | 4 | 5 | 1 |
| 0 | 2 | 9 | 5 |
Найти седловую точку (указать оптимальные стратегии игроков).
№ 13
| -2 | 4 | -3 | 1 |
| 5 | 0 | 0 | 2 |
| 3 | 2 | -1 | 6 |
| 4 | 6 | 0 | -2 |
№ 15
| 2 | 1 | 3 | 5 |
| 4 | 5 | 5 | 4 |
| 6 | 8 | 6 | 6 |
| 9 | 1 | 1 | 7 |
№ 19
| 8 | 7 | 2 | 1 |
| 3 | 4 | 4 | 4 |
| 5 | 5 | 4 | 2 |
| 9 | 7 | 5 | 4 |
№ 20
| 4 | 3 | 6 | 5 |
| 3 | 2 | 8 | 0 |
| 5 | 0 | 4 | 3 |
| 1 | 1 | 5 | 7 |
№ 22
| 3 | 0 | 6 | 7 |
| 2 | 2 | 4 | 5 |
| 6 | 1 | 2 | 2 |
| 5 | 5 | 5 | 5 |
Определить количество седловых точек в игре.
№ 17
| 2 | 1 | 3 | 2 |
| 1 | 1 | 1 | 1 |
| 3 | 2 | 2 | 2 |
| 1 | 1 | 3 | 2 |
№ 18
| -1 | 0 | 1 | -2 |
| 1 | 2 | 0 | -2 |
| 1 | 2 | 2 | 1 |
| 1 | 3 | 3 | 1 |
№ 21
| 2 | 3 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 2 | 2 | 3 | 2 |
| 2 | 4 | 1 | 2 |
Сократите, если возможно, данную платежную матрицу. До каких размеров сократилась матрица? Ответ введите в виде двух чисел (количество строк и количество столбцов).
№ 24
| 8 | 7 | 2 | 5 |
| 3 | 4 | 4 | 4 |
| 5 | 5 | 4 | 2 |
| 9 | 7 | 5 | 4 |
№ 25
| 5 | 3 | 2 | 4 |
| 7 | 6 | 0 | 4 |
| 2 | 8 | 3 | 3 |
| 9 | 2 | 2 | 2 |
№ 26
| 5 | 2 | 4 | 4 |
| 3 | 9 | 2 | 0 |
| 7 | 6 | 8 | 8 |
| 5 | 2 | 8 | 3 |
№ 27
| 5 | 2 | 1 | 4 |
| 4 | 5 | 3 | 3 |
| 2 | 5 | 5 | 6 |
| 7 | 3 | 0 | 2 |
№ 28
Какой из предложенных методов решения антагонистических игр является приближенным?
• итеративный.
№ 29
Какой из предложенных методов решения антагонистических игр предназначен для решения игр размерностью 2х2?
• аналитический.
№ 30
Какой из предложенных методов решения антагонистических игр является точным и универсальным?
• линейного программирования.
№ 31
Можно ли решить данную игру аналитическим методом?
| 8 | 7 | 2 | 5 |
| 3 | 4 | 4 | 4 |
| 5 | 5 | 4 | 2 |
| 9 | 7 | 5 | 4 |
Можно ли решить данную игру графическим методом?
№ 32
| 5 | 2 | 4 | 4 |
| 3 | 9 | 2 | 0 |
| 7 | 6 | 8 | 8 |
| 5 | 2 | 8 | 3 |
№ 33
| 5 | 2 | 1 | 4 |
| 2 | 5 | 3 | 3 |
| 2 | 5 | 5 | 6 |
| 7 | 3 | 1 | 2 |
№ 34
| 4 | 10 | 3 | 3 |
| 5 | 3 | 2 | 1 |
| 1 | 2 | 9 | 8 |
| 5 | 7 | 4 | 2 |
№ 35
Какая из форм представления игр является наиболее наглядной для описания многоходовой игры?
• позиционная форма игры.
№ 36
Какая из форм представления игр является наиболее наглядной для описания конечной антагонистической игры?
• матричная форма игры.
№ 37
В какой форме обычно представляют кооперативные игры?
• в форме характеристической функции.
№ 38
Какая из форм представления игр является наиболее наглядной для описания бесконечной антагонистической игры?
• нормальная форма игры.
№ 39
Какая из форм представления игр является наиболее наглядной для описания некооперативной игры двух лиц?
• матричная форма игры.
№ 40
В какой форме должна быть представлена многоходовая антагонистическая игра с полной информацией для нахождения решения?
• в позиционной.
№ 41
В какой форме должна быть представлена многоходовая антагонистическая игра с неполной информацией для нахождения решения?
• в матричной.
№ 42
Какая из форм представления игр является наиболее наглядной для описания некооперативной игры трех лиц?
• нормальная форма игры.
№ 43
Бесконечная игра трех лиц может быть представлена:
• только в нормальной форме.
№ 44
Кооперативная игра двух лиц может быть представлена:
• в матричной форме и в форме характеристической функции.
Дана бесконечная антагонистическая игра:
№ 45
Г=<[1,3],[0,1],x2+y2>. Является ли данная игра игрой на единичном квадрате?
• да.
№ 46
Г=<[1,3],[0,1],x2+y2>. Данная игра является:
• выпуклой.
№ 47
Г=<[0,1],[0,1],x2-y2+xy>. Данная игра:
• не относится к выпуклой, вогнутой и выпукло-вогнутой.
№ 48
Г=<[-1,1],[0,1],2xy-x2+y2. Данная игра является:
• выпукло-вогнутой.
№ 49
Г=<[0,1],[1,2.3],x2+y2+xy>. Является ли данная игра игрой на единичном квадрате?
• нет.
№ 50
Г=<[-1,3],[0,2],3x-x3-y2. Данная игра является:
• вогнутой.
№ 51
Г=<[1,3],[0,1],x2+y2-5xy>. В данной игре решение в чистых стратегиях имеется:
• у второго игрока.
№ 52
Г=<[1,3],[0,1],2y-3x2+y2+xy>. В данной игре решение в чистых стратегиях имеется:
• у обоих игроков имеется решение в чистых стратегиях.
№ 53
Г=<[1,3],[0,1],x2-y2-4xy+2y>. В данной игре решение в чистых стратегиях имеется:
• у обоих игроков решение имеется только в смешанных стратегиях.
№ 54
Г=<[1,3],[0,1],6xy-x2-y2>. В данной игре решение в чистых стратегиях имеется:
• у первого игрока.
№ 55
Г=<[-1,3],[0,2],3x+x3-y2>. Данная игра:
• не относится к выпуклой, вогнутой и выпукло-вогнутой.
Дана некооперативная игра двух лиц:
Определить точку status quo
№ 56
| A | B | ||||
| 4 | 3 | 2 | 5 | 2 | 2 |
| 6 | 5 | 4 | 4 | 3 | 4 |
| 3 | 5 | 3 | 7 | 1 | 5 |
№ 58
| A | B | ||||||
| 4 | 3 | 2 | 4 | 5 | 7 | 1 | 8 |
| 6 | 2 | 5 | 0 | 3 | 6 | 2 | 4 |
№ 60
| A | B | ||||
| 7 | -2 | 2 | 2 | 1 | 1 |
| 4 | 4 | 5 | 1 | -2 | 1 |
| 2 | 2 | 3 | 2 | 1 | 1 |
№ 62
| A | B | ||||||
| 4 | 2 | 3 | 2 | 6 | 3 | 4 | 7 |
| 2 | 3 | 1 | 2 | 5 | 2 | 3 | 4 |
№ 64
| A | B | ||||||
| 5 | 5 | 4 | 7 | 0 | 2 | -1 | 4 |
| 3 | 2 | 4 | 0 | -2 | 2 | 1 | 3 |
| 6 | 0 | 1 | 8 | -1 | -3 | 0 | 0 |
№ 66
| A | B | ||||||
| 5 | 3 | 0 | -4 | 7 | 4 | 2 | 4 |
| 6 | 5 | 2 | 3 | 6 | 6 | 3 | 6 |
| 0 | 4 | 2 | 8 | 9 | 1 | 2 | 3 |
Определить оптимальные стратегии игроков
№ 57
| A | B | ||||
| 4 | 3 | 2 | 3 | 2 | 5 |
| 0 | 5 | 3 | 4 | 3 | 4 |
| 3 | 5 | 3 | 7 | 4 | 5 |
№ 59
| A | B | ||||||
| 1 | 1 | 2 | 5 | 0 | 3 | 1 | 4 |
| 4 | 4 | -3 | 5 | -2 | -1 | 2 | 5 |
№ 61
| A | B | ||||
| 3 | 4 | -2 | 7 | 2 | 5 |
| 9 | 3 | 4 | 2 | 3 | 3 |
| 7 | 5 | 6 | 6 | 8 | 4 |
№ 63
| A | B | ||
| 0 | 0 | 5 | 3 |
| 3 | 2 | 4 | 6 |
№ 65
| A | B | ||||
| 6 | 7 | 5 | 2 | 6 | 0 |
| 0 | 0 | 1 | 0 | -2 | 1 |
| 8 | 6 | -2 | 1 | 2 | 2 |
| 6 | 1 | 0 | 1 | 5 | 1 |
№ 67
| A | B | ||||
| 2 | 4 | 6 | 4 | 5 | 5 |
| 3 | 0 | 5 | 7 | 0 | 6 |
| 3 | 4 | 3 | 4 | 7 | 2 |
| 2 | 9 | 0 | 2 | 9 | 3 |
Дана кооперативная игра трех лиц:
№ 68
X={1,2,3},Y={2,4,6},Z={0,3}
Jx=Jy=Jz=x+y+z
Определить характеристическую функцию коалиции {x,y}.
• (18)
№ 69
X={1,2,3},Y={2,4,6},X={0,3}
Jx=Jy=Jz=x+y+z
Определить характеристическую функцию максимальной коалиции.
• (36)
№ 70
X={1,2,3},Y={2,4,6},Z={0,1,3}
Jx=2xy-yz, Jy=Jz=x+y+z
Определить характеристическую функцию коалиции {x}.
• (6)
№ 71
X={1,3},Y={0,2,4,6},Z={0,3}
Jx=Jy=xy-2z, Jz=x+y+z
Определить характеристическую функцию коалиции {y,z}.
• (13)
№ 72
X={0,2,5},Y={2,4},Z={0,3,4}
Jx=Jy=Jz=xz+y-z
Определить характеристическую функцию коалиции {y}.
• (0)
№ 73
X={1,2,3},Y={2,4,6},Z={0,3}
Jx=x+z, Jy=y+x, Jz=y+z
Определить характеристическую функцию коалиции {x,z}.
• (11)
№ 74
X={1,2},Y={2,4,6,8},Z={0,1,3}
Jx=Jy=Jz=x+y-z
Определить характеристическую функцию максимальной коалиции.
• (30)
№ 75
X={1,2,3},Y={2,4,6},Z={0,3}
Jx=xy-z, Jy=y-z, Jz=x+y+z
Определить характеристическую функцию коалиции {x,y}.
• (18)
№ 76
X={1,2,3},Y=Z={2,4,6}
Jx=Jy=x+y+z, Jz=2z-x-y
Определить характеристическую функцию коалиции {z}.
• (3)
№ 77
X={1,2,3},Y={2,4,6},Z={0,3}
Jx=Jy=Jz=x+y+z
Определить характеристическую функцию коалиции {x,z}.
• (16)
№ 78
X={1,2,3},Y={2,4,6},Z={0,3}
Jx=xy-z, Jy=y-z, Jz=x+y+z
Определить характеристическую функцию максимальной коалиции.
• (33)
№ 79
X={1,2,3},Y=Z={2,4,6}
Jx=Jy=x+y+z, Jz=2z-x-y
Определить характеристическую функцию коалиции {x,y}.
• (22)
Дана кооперативная игра трех лиц в форме характеристической функции:
№ 80
νx=2, νy=1, νz=2, νxy=5, νxz=6, νyz=7, νxyz=10
Для данной игры справедливо высказывание:
• C-ядро существует.
№ 81
νx=3, νy=1, νz=0, νxy=10, νxz=16, νyz=12, νxyz=18
Для данной игры справедливо высказывание:
• C-ядро не существует: не выполняется дополнительное условие по двойным коалициям.
№ 82
νx=4, νy=5, νz=2, νxy=8, νxz=10, νyz=8, νxyz=14
Для данной игры справедливо высказывание:
• C-ядро не существует: не выполняется условие супераддитивности.
№ 83
νx=0, νy=3, νz=2, νxy=5, νxz=6, νyz=7, νxyz=10
Пометьте вектора, которые являются дележами данной игры:
• (3,3,4);
• (1,5,4).
№ 84
νx=6, νy=4, νz=5, νxy=12, νxz=12, νyz=11, νxyz=20
Пометьте вектора, которые являются дележами данной игры:
• (10,5,5);
• (6,7,7).
№ 85
νx=1, νy=0, νz=2, νxy=4, νxz=6, νyz=4, νxyz=10
Пометьте вектора, которые являются дележами данной игры:
• (3,0,7);
• (1,7,2);
• (3,3,4.
№ 86
νx=2, νy=2, νz=2, νxy=15, νxz=12, νyz=14, νxyz=18
Пометьте вектора, которые являются дележами данной игры:
• (6,6,6);
• (3,12,3).
№ 87
νx=3, νy=3, νz=1, νxy=7, νxz=6, νyz=8, νxyz=12
Рассмотрим следующие дележи:
a=(4,4,4), b=(3,3,6), c=(6,3,3),
Правильные условия доминирования:
![]() .
.
№ 88
νx=2, νy=0, νz=1, νxy=8, νxz=6, νyz=4, νxyz=10
Рассмотрим следующие дележи:
a=(3,5,2), b=(2.5,4,3.5), c=(2,5,3),
Правильные условия доминирования:
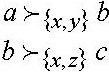 .
.
№ 89
νx=0, νy=3, νz=1, νxy=8, νxz=10, νyz=10, νxyz=16
Рассмотрим следующие дележи:
a=(6,5,5), b=(9,4,3), c=(2,6,8), d=(1,5,10)
Правильные условия доминирования:
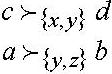 .
.
Дана кооперативная игра двух лиц в форме характеристической функции:
№ 90
ν1=2, ν2=1.5, ν1=5
Определить вектор Шепли.
• (2.75, 2.25)
№ 91
ν1=1, ν2=3.5, ν1=4
Определить вектор Шепли.
• (0.75, 3.25)
№ 92
ν1=3, ν2=5, ν1=12
Определить вектор Шепли.
• (5, 7)
№ 93
ν1=4, ν2=2, ν1=8
Определить вектор Шепли.
• (5, 3)
№ 94
ν1=1, ν2=2.5, ν1=4
Определить N-ядро игры.
• (1.25, 2.75)
№ 95
ν1=12, ν2=7, ν1=20
Определить N-ядро игры.
• (12.5, 7.5)
№ 96
ν1=2, ν2=4.5, ν1=12
Определить вектор Шепли.
• (4.75, 7.25)
№ 97
ν1=8, ν2=12, ν1=18
Определить вектор Шепли.
• (7, 11)
№ 98
ν1=12, ν2=10, ν1=34
Определить N-ядро игры.
• (18, 16)
№ 99
ν1=7, ν2=9, ν1=20
Определить N-ядро игры.
• (9, 11)
№ 100
ν1=10, ν2=8, ν1=28
Определить вектор Шепли.
• (15, 13)
| на главную | база по специальностям | база по дисциплинам | статьи |
Другие статьи по теме
