Системный анализ и исследование операций
для специальности 230102 (220200)
Разработка управленческих решений
для специальности 080504
Теория принятия решений
для специальности 230102
Кафедра АОИ
Турунтаев Л.П.
Томск-2007

Основы методологии разработки управленческих решений.

№ 1
Процесс разработки и принятия управленческих решений с технологической точки зрения включает этапы:
• выявление и описание проблемной ситуации, формирование целей системы управления, генерация альтернативных решений, формирование критериев выбора решений, оценка возможных решений, принятие (выбор) решения, контроль исполнения и анализ последствий от принятого решения.

№ 2
Системный анализ –
• практический раздел системных исследований проблем в сфере организационного управления, для решения которых отсутствуют отработанные способы их решения.

№ 3
Исследование операций –
• научная дисциплина количественного обоснования принимаемых решений на базе методов математического моделирования.

№ 4
Что первично в теории принятия решений?
• Проблема.

№ 5
Для нетривиальной задачи принятия решений (ЗПР) характерно:
• Один критерий оценки решений и множество возможных ситуаций (исходов) реализации решений.
• Множество критериев оценки решений и множество возможных ситуаций реализации решений.
• Множество критериев оценки решений и одна ситуация реализации решений.

№ 6
К типовым задачам исследования операций можно отнести следующие:
• управления запасами, упорядочения и согласования, распределительные.

№ 7
Основным предположением использования критериального языка обоснования решений является:
• альтернативу можно оценить конкретным числом через критерий эффективности.

№ 8
- использования языка бинарных отношений:
• альтернативы должны быть взаимно независимыми.

№ 9
Задачи принятия решений в условиях определенности отличаются от задач принятия решений в условиях неопределенности тем, что:
• в первом случае – исход решения задачи описывается однозначно, во втором – через множество возможных состояний системы.

№ 10
В зависимости от новизны проблемной ситуации решения делятся на:
• стандартные, оригинальные, усовершенствованные.

Генерация и измерение решений.

№ 11
В чем особенность генерации решений для хорошо формализуемых задач управления?
• Генерируемое множество допустимых решений определяется математическими зависимостями в виде имитационной модели задачи управления.

№ 12
К методам генерации решений относятся следующие методы:
• мозгового штурма;
• когнитивных карт;
• деловые игры.

№ 13
Принципиальное отличие метода мозгового штурма от синектического метода генерирования альтернатив:
• Метод мозгового штурма разработан для генерирования максимального количества альтернатив в отличие от синектического метода.
• При синектическом методе генерирования альтернатив в обсуждении экспертами допускается критика высказываний в отличие от метода мозгового штурма.

№ 14
Идея метода морфологического анализа генерации решений:
• В генерации альтернативных решений путем перебора возможных сочетаний значений параметров проектируемой системы.

№ 15
Идея метода когнитивных карт:
• В изучении стабильности работы системы управления и определения альтернатив её устойчивой работы на основе анализа знакового графа причинных связей между основными элементами данной системы.

№ 16
Экспертные методы измерения объектов:
• Метод парных сравнений.
• Метод ранжирования.

№ 17
Основание для применения аксиоматического подхода оценки полезности решений:
• Аксиомы независимости альтернатив по полезности.
• Аксиомы взаимной независимости критериев оценки альтернатив.

№ 18
Функция полезности может быть определена:
• На множестве альтернатив.
• На множестве критериев.

№ 19
Измерительные шкалы:
• Ранговые, отношений, абсолютные.

№ 20
Особенности интервальной шкалы и шкалы отношений:
• Интервальная шкала и шкала отношений – это количественные шкалы измерения объектов.

Моделирование однокритериальных задач принятия решений в условиях определенности.

№ 21
Математическое программирование - это:
• раздел математики, изучающий поиск решений задач на оптимизационных математических моделях.

№ 22
Для оптимизационных и имитационных математических моделей обоснования решений характерно:
• Оптимизационные модели позволяют сгенерировать альтернативные решения и оценить их через критерии оптимальности, а имитационные модели позволяют только сгенерировать альтернативные решения.
• Имитационная модель представляет собой систему уравнений и ограничений, описывающих состояние исследуемой системы через её входные и выходные параметры.

№ 23
Областью генерируемых (допустимых) решений задач линейного программирования является:
• многоугольная выпуклая область решений, заданная системой ограничений на управляемые переменные.

№ 24
Верная содержательная постановка транспортной задачи линейного программирования:
• Имеется m поставщиков и n потребителей однородной продукции, возможности и потребности которых соответственно равны a_i и b_j, i=1;m, j=1;n. Стоимость перевозки одной единицы продукции из пункта i в пункт j равна C_ij. Определить план перевозки продукции от поставщиков к потребителям, минимизирующий общую стоимость всех перевозок.

№ 25
- задачи линейного программирования о назначениях:
• Имеется m потенциальных исполнителей (j=1;m) соответственно одной из имеющихся m работ (i=1;m). Известны затраты c_ij на выполнение j-м исполнителем i-й работы. Требуется назначить каждого исполнителя на одну работу так, чтобы минимизировать суммарные затраты.

№ 26
Чем отличаются математические постановки задач о назначениях и о коммивояжере?
• В математической постановке задачи о коммивояжере присутствует условие исключения подциклов.

№ 27
Рассматривается задача оптимизации плана производства нефтепродуктов, описанная в виде модели линейного программирования. Объём производства измеряется в тоннах. Задача решается на минимум издержек. Учитывается ограничение на время использования оборудования. В каких единицах измеряется значение коэффициентов матрицы для этого ограничения?
• Час/тонн.

№ 28
- В результате решения лимитирующим фактором оказалась мощность оборудования, измеряемая в тоннах перерабатываемой нефти. В каких единицах измеряется двойственная оценка соответствующего ограничения?
• Руб./тонн.

№ 29
Для приготовления вина “Букет роз” используется смесь из белого и красного сухих вин. Белого вина в готовой смеси должно быть не более 30%. Пусть x – количество белого вина, которое следует использовать для приготовления смеси, y – количество красного вина. Условие на содержание ингредиентов в готовой смеси:
• 0.7x <= 0.3y.

№ 30
Рассматривается задача о смесях. В задаче смешения исходными ингредиентами являются бензины марок А, В и С, октановые числа которых 76, 93 и 98. Октановое число смеси должно быть не менее 93. Какое неравенство формализует это условие, если за x1, x2и x3 приняты предназначенные для смешения количества бензинов А, В и С соответственно?
• 5x3 - 17x1 >=0.

Решение задач линейного программирования.

№ 31
Решить задачу графически. Ответ в виде двух чисел (значение x₁; значение x₂).
-x₂→min.
x₁+x₂≥1.
x₁+x₂≤2.
x₁-x₂≤1.
x₁-x₂≤-1.
x₁, x₂≥0.
• (0;2)

№ 32
Дана исходная задача линейного программирования.
2x₁+3x₂→min.
-5x₁+3x₂≤15.
x₁-2x₂≥4.
x₁, x₂≥0.
Если каждое из ограничений модели связано с ограничением на соответствующий ресурс, то какие из ресурсов (ограничений) являются дефицитными?
• Второй.

№ 33
- Какая задача будет являться к ней двойственной, если y₁, y₂ - двойственные оценки ограничений?
• 15y₁-4y₂→min.
5y₁+y₂≤2.
-3y₁-2y₂≤3.
y₁, y₂≥0.

№ 34
Дана транспортная задача линейного программирования (возможности поставщиков и потребности потребителей заданы справа и внизу матрицы).

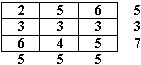
Оценить оптимальный план решения задачи, указав суммарные затраты на перевозку.
• (49)

№ 35
В задаче линейного программирования о назначениях известны затраты на выполнение каждым исполнителем соответствующих работ (три исполнителя и три работы).

17	26	5
10	9	14
16	23	24

Суммарные затраты на выполнение всех работ:
• (23)

№ 36
Дана матрица расстояний между четырьмя городами («-» означает, что переезд по маршруту закрыт).

-	4	6	5
4	-	8	8
5	6	-	3
7	7	4	-

Оцените оптимальный план решения задачи о коммивояжере, указав суммарные затраты на объезд всех городов с возвращением в исходный город.
• (19)

№ 37
(«-» означает, что дорогу проложить невозможно).

-	3	-	1
3	-	5	-
6	5	-	3
2	-	4	-

Необходимо проложить сеть дорог наименьшей протяженностью, позволяющей попасть в любой из городов.Протяженность:
• (8)

№ 38
Сеть с истоком в вершине 1 и стоком в вершине 5. Задана функция пропускных способностей сети в виде матрицы смежности, («-» означает, что дуга закрыта).

-	-	-	-	-
2	-	-	-	-
3	4	-	-	-
5	1	2	-	-
-	2	3	3	-

Оцените величину пропускной способности по разрезу сети r(Z,S), где Z и S – множество вершин; Z = {1,2,3}, S={4,5}
• (13)

№ 39
Сетевой график в терминах событий с указанием длительности выполнения работ в виде матрицы смежности. Вершина 1 – начальное событие, вершина 5 – конечное событие.

-
1	-
2	2	-
	3		-
	4	3	1	-

Длина критического пути:
• (6)

№ 40
Распределить ресурс объёмом в 40 единиц между двумя предприятиями таким образом, чтобы суммарный доход от использования выделенных ресурсов предприятиям был бы максимальным.

Объём выделяемого ресурса	Доход предприятия 1	Доход предприятия 2
0	0	0
10	9	8
20	20	19
30	31	30
40	37	38

Суммарный доход предприятий:
• (39)

Решение многокритериальных задач принятия решений в условиях определенности.

№ 41
Решается транспортная задача перевозки однородных грузов от поставщиков к потребителям (размерность задачи два на два) с учетом двух критериев: К1 – финансовые затраты (т.руб.); К2 – временные затраты (час.). Возможности поставщиков - a1 и a2 , потребности потребителей – b1 и b2, коэффициенты затрат на одну единицу груза для соответствующих критериев приведены в таблицах.

1	4	b1=3
2	3	b2=7
a1=5	a2=5

5	2	b1=3
4	3	b2=7
a1=5	a2=5

В каких пределах будет изменяться оценка компромиссных решений по критерию К1 (нижняя оценка, верхняя оценка).
• (22;28)

№ 42
- по критерию К2.
• (32;38)

№ 43
- Значимость критериев К1 и К2 оценивается через весовые коэффициенты, их взять соответственно 0,8 и 0,2. Нормализацию коэффициентов матриц затрат для соответствующих критериев производить соответственно через максимальные коэффициенты соответствующих матриц.
Оцените через критерии К1 (т.руб.) и К2 (час.) компромиссное решение, найденное по принципу взвешенной суммы двух критериальных функций К1 и К2 (оценка компромиссного решения по критерию К1, оценка компромиссного решения по критерию К2).
• (22;38)

№ 44
Решается задача о назначениях работ их потенциальным исполнителям (размерность задачи два на два) с учетом двух критериев: К1 – финансовые затраты (т.руб.); К2 – временные затраты (час.). Матрицы затрат выполнения каждой работы каждым исполнителем по указанным критериям приводятся ниже.

1	4
2	3

5	2
4	3

В каких пределах будет изменяться оценка компромиссных решений по критерию К1 (нижняя оценка, верхняя оценка).
• (4;6)

№ 45
- по критерию К2.
• (6;8)

№ 46
Тренер гандбольной команды решает выставить на предстоящую игру персонально против трех игроков О1, О2 и О3 команды соперника своих трех игроков С1, С2 и С3. Возможности своих игроков (субъектов) и возможности игроков команды соперника (объектов) тренер оценивает по трем критериям:
1. бег 100 метров (сек.);
2. рост (см.);
3. выносливость (низкая - 3, средняя - 4, высокая -5).

	Субъект	С1	С2	С3
Критерии	1	11	12	15
Критерии	2	172	175	190
Критерии	3	4	4	4
	Объект	О1	О2	О3
Критерии	1	11	11	12
Критерии	2	180	170	185
Критерии	3	3	3	5

Определите один из вариантов расстановки игроков, близких по своим показателям. Укажите номер соперника для каждого игрока команды.
• (2,3; 1; 2,3)

№ 47

	Субъект	С1	С2	С3
Критерии	1	15	12	11
Критерии	2	190	175	174
Критерии	3	4	4	4
	Объект	О1	О2	О3
Критерии	1	11	11	12
Критерии	2	180	173	185
Критерии	3	3	3	5

• (2,1; 3; 1,2)

№ 48
Имеются три потенциальных исполнителя и три работы. Исполнители С1, С2 и С3 могут быть назначены на одну из трех работ О1, О2, О3. Назначение зависит от возможностей исполнителей и требований к выполняемым работам. Характеристики на исполнителей и на работы приведены по трем критериям.
1. Время выполнения (быстро – 5, не быстро – 4, медленно – 3).
2. Качество выполнения (отличное – 5, хорошее – 4, удовлетворительное – 3).
3. Оплата труда (высокая – 3, средняя – 4, низкая – 5).

	Исполнитель	С1	С2	С3
Критерии	1	5	4	3
Критерии	2	3	4	5
Критерии	3	4	4	4
	Работа	О1	О2	О3
Критерии	1	5	5	4
Критерии	2	4	3	4
Критерии	3	3	3	5

Определите один из вариантов назначения исполнителей на работу. Укажите номер исполнителя для каждoй работы.
• (2,3; 1; 2,3)

№ 49

	Исполнитель	С1	С2	С3
Критерии	1	4	5	3
Критерии	2	4	3	5
Критерии	3	4	4	4
	Работа	О1	О2	О3
Критерии	1	5	5	4
Критерии	2	3	4	4
Критерии	3	3	3	5

• (2; 1,3; 3,1)

№ 50
Имеются три потенциальных сотрудника организации С1, С2 и С3 и три вакантные должности О1, О2, О3. Расстановка кадров производится в соответствии с возможностями претендентов и требованиями со стороны организации. Оценки возможностей субъектов (назначаемых сотрудников) и объектов (должностей) приведены по трем критериям.
1. Профессиональная подготовленность (высокая – 5, средняя – 4, низкая - 3).
2. Умение руководить коллективом (высокое – 5, среднее – 4, низкое - 3).
3. Практический опыт (большой – 5, небольшой – 4, отсутствует – 3).

	Сотрудник	С1	С2	С3
Критерии	1	4	3	5
Критерии	2	4	5	3
Критерии	3	4	4	4
	Работа	О1	О2	О3
Критерии	1	5	5	4
Критерии	2	4	3	4
Критерии	3	3	3	5

• (2,1; 3; 1,2)

Принятие решений на языке бинарных отношений.

№ 5
Владелец бензоколонки думает о том, каков должен быть размер его станции: Х1 – маленькая станция, Х2 – небольшая, Х3 – средняя, Х4 – большая. В результате анализа возможных состояний рынка сбыта (е1 - хороший рынок, е2 - средний рынок, е3 - плохой рынок) он оценил возможные исходы решений в виде матриц парных сравнений, в которых цифра 1 означает, что альтернатива по строке не уступает альтернативе по столбцу.

Укажите наилучший вариант решения, используя критерий Байеса.
• X2.
• X3.

№ 5
Магазин «Молоко» продает в розницу молочные продукты. Директор магазина должен определить, сколько бидонов сметаны следует закупить у производителя для торговли в течение недели. Вероятности того, что спрос на сметану в течение недели будет 7; 8 и 9 бидонов, равны соответственно 0,2; 0,3; 0,5. Результат анализа возможных состояний рынка сбыта (е1 – спрос на 7 бидонов, е2 - спрос на 8 бидонов, е3 - спрос на 9 бидонов).

Сколько бидонов сметаны следует закупить у производителя для торговли в течение недели?
• (8)

№ 51
Оценка игроков спортивной команды (альтернатив) производится на основании пяти критериев, перечисленных в порядке убывания их значимости: К1 - морально-волевая подготовка; К2 – вес игрока; К3 – бег 100м; К4 – психологическая подготовка; К5 – рост игрока. Оценки игроков по критериям приведены в таблице.

Игроки	Х1	Х2	Х3
Мор-волевая (в баллах)	10	5	8
Вес (в кг)	100	110	90
Бег 100м (в сек.)	15	14	13
Псих.подготовка (шкала наимен.)	Низкая	Средняя	Высокая
Рост (в см.)	200	210	190

Тренер отдает предпочтение игрокам с высокими оценками по всем критериям (для бега – оценки имеют обратное направление шкалы). Установите на множестве альтернатив отношение Парето, по порядку указанному в матрице. (1 – есть отношение, 0 – нет отношения)

Парето
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (0;0;0;0;0;0)

№ 52
- мажоритарное отношение.

Мажоритарное
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (1;0;0;1;1;0)

№ 53
- лексикографическое отношение.

Лексикографическое
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (0;0;1;1;1;0)

№ 54

Игроки	Х1	Х2	Х3
Мор-волевая (в баллах)	4	5	8
Вес (в кг)	80	110	90
Бег 100м (в сек.)	14	14	13
Псих.подготовка (шкала наимен.)	Низкая	Средняя	Высокая
Рост (в см.)	180	210	190

- отношение Парето.

Парето
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (1;1;0;0;0;0)

№ 55
- мажоритарное отношение.

Мажоритарное
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (1;1;0;1;0;0)

№ 56
- лексикографическое отношение.

Лексикографическое
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (1;1;0;1;0;0)

№ 63
Оценки игроков по критериям в таблице приведены в абсолютной шкале измерения.

Игроки	Х1	Х2	Х3
Мор-волевая (в баллах)	0	1	0
Вес (в кг)	0	1	1
Бег 100м (в сек.)	1	0	0
Псих.подготовка (шкала наимен.)	0	1	0
Рост (в см.)	0,6	1	0

- отношения Подиновского без учета значимости критериев.

Подиновского
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (1;1;0;0;0;1)

№ 64
- отношения Подиновского с учетом значимости критериев.

Подиновского
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (1;1;0;0;0;1)

№ 65

Игроки	Х1	Х2	Х3
Мор-волевая (в баллах)	0	0	1
Вес (в кг)	0	1	1
Бег 100м (в сек.)	1	0	0
Псих.подготовка (шкала наимен.)	0	1	0
Рост (в см.)	1	1	0

- отношения Подиновского без учета значимости критериев.

Подиновского
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (1;1;0;0;0;1)

№ 66
- отношения Подиновского с учетом значимости критериев.

Подиновского
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (1;1;0;0;0;0)

№ 67
Малый производитель ряда продуктов из сыра определяет, сколько ящиков сыра производить каждый месяц. Вероятность, что спрос будет 6 ящиков, равна 0.2, семь —0.3 и восемь —0.5.В результате анализа возможных состояний рынка сбыта (е1 – спрос на 6 ящиков, е2 - спрос на 7 ящиков, е3 - спрос на 8 ящиков) он оценил возможные исходы решений в виде матриц парных сравнений, в которых цифра 1 означает, что альтернатива по строке не уступает альтернативе по столбцу.

Сколько ящиков сыра должно производиться каждый месяц? (используется критерий Байеса)
• (7)

№ 68
Оценка игроков спортивной команды: К1 - морально-волевая подготовка; К2 – вес игрока; К3 – бег 100 м; К4 – психологическая подготовка; К5 – рост игрока. Значимость критериев представлена соответственно величинами: 15; 13; 10; 7; 5.
Определите индексы согласия доминирования альтернатив по методу “Электра”. Ответ в виде матрицы индексов согласия в десятичных дробях с точностью до сотых долей, например 0.33.

Индексы согласия
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (0.7;0.34;0.3;0.64;0.66;0.36)

№ 69
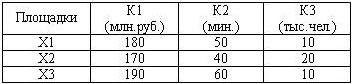
Предлагается построить аэропорт недалеко от города в одном из трех возможных мест расположения: Х1, Х2 и Х3. Оценка вариантов постройки аэропорта производилась по трем критериям: К1 – стоимость постройки; К2 – время в пути до центра города; К3 – количество людей, подвергающихся шумовым воздействиям. Значимость критериев представлена соответственно величинами: 6; 3; 1.

Индексы согласия
	Х1	Х2	Х3
Х1	-	(3)	(5)
Х2	(1)	-	(6)
Х3	(2)	(4)	-

• (0.9;0.1;0.1;0.1;1;0.9)

№ 70

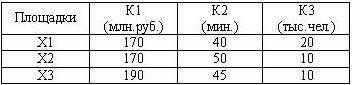
• (0.7;0.1;0.9;0.4;0.9;0.7)

Принятие решений на языке функций выбора.

№ 71
Оценка научно-технических проектов производится по четырем критериям, измеряемых в шкале наименований (в скобках дана шкала в порядке убывания предпочтения): К1 – ожидаемая экономическая эффективность (высокая, средняя, низкая); К2 – срок выполнения проекта (менее 3-х лет, от 3-х до 5-ти лет, более 5-ти лет); К3 – срок окупаемости проекта (менее 2-х лет, от 2-х до 5-ти лет, более 5-ти лет); К4 – масштаб внедрения (за рубежом, в стране, в своём регионе). Оценки проектов по критериям приведены в таблице.

Проекты	Х1	Х2	Х3
Ожид.экон. эффективн.	Средняя	Высокая	Низкая
Срок выполнения	менее 3-х лет	более 5-ти лет	менее 3-х лет
Срок Окупаемости	менее 2-х лет	от 2-х до 5-ти лет	более 5-ти лет
Масштаб внедрения	в стране	за рубежом	в своём регионе

По функции выбора с учетом числа доминирующих критериев определить подмножество наилучших проектов.
• Х1.
• Х2.

№ 72

Проекты	Х1	Х2	Х3
Ожид.экон. эффективн.	Высокая	Средняя	Низкая
Срок выполнения	более 5-ти лет	менее 3-х лет	менее 3-х лет
Срок Окупаемости	от 2-х до 5-ти лет	менее 2-х лет	более 5-ти лет
Масштаб внедрения	за рубежом	в стране	в своём регионе

• Х1.
• Х2.

№ 73

Проекты	Х1	Х2	Х3
Ожид.экон. эффективн.	Высокая	Низкая	Средняя
Срок выполнения	более 5-ти лет	менее 3-х лет	менее 3-х лет
Срок Окупаемости	от 2-х до 5-ти лет	более 5-ти лет	менее 2-х лет
Масштаб внедрения	за рубежом	в своём регионе	в стране

• Х1.
• Х3.

№ 74

Проекты	Х1	Х2	Х3
Ожид.экон. эффективн.	Высокая	Низкая	Средняя
Срок выполнения	более 5-ти лет	менее 3-х лет	от 3-х до 5-ти лет
Срок Окупаемости	от 2-х до 5-ти лет	более 5-ти лет	менее 2-х лет
Масштаб внедрения	за рубежом	в своём регионе	в стране

• Х1.
• Х3.

№ 75

Проекты	Х1	Х2	Х3
Ожид.экон. эффективн.	Высокая	Низкая	Средняя
Срок выполнения	от 3-х до 5-ти лет	менее 3-х лет	от 3-х до 5-ти лет
Срок Окупаемости	от 2-х до 5-ти лет	более 5-ти лет	менее 2-х лет
Масштаб внедрения	за рубежом	за рубежом	в стране

• Х1.

№ 76

Проекты	Х1	Х2	Х3
Ожид.экон. эффективн.	Высокая	Низкая	Средняя
Срок выполнения	более 5-ти лет	менее 3-х лет	от 3-х до 5-ти лет
Срок Окупаемости	от 2-х до 5-ти лет	более 5-ти лет	менее 2-х лет
Масштаб внедрения	за рубежом	в своём регионе	в стране

По функции выбора методом идеальной точки в ранговой шкале измерений определить наилучший проект (проекты). Веса критериев считать равнозначными.
• Х3.

№ 77

Проекты	Х1	Х2	Х3
Ожид.экон. эффективн.	Средняя	Высокая	Низкая
Срок выполнения	менее 3-х лет	более 5-ти лет	от 3-х до 5-ти лет
Срок Окупаемости	менее 2-х лет	от 2-х до 5-ти лет	более 5-ти лет
Масштаб внедрения	в стране	за рубежом	в своём регионе

• Х1.

№ 78

Проекты	Х1	Х2	Х3
Ожид.экон. эффективн.	Высокая	Средняя	Низкая
Срок выполнения	более 5-ти лет	от 3-х до 5-ти лет	менее 3-х лет
Срок Окупаемости	от 2-х до 5-ти лет	менее 2-х лет	более 5-ти лет
Масштаб внедрения	за рубежом	в стране	в своём регионе

• Х2.

№ 79

Проекты	Х1	Х2	Х3
Ожид.экон. эффективн.	Высокая	Низкая	Средняя
Срок выполнения	более 5-ти лет	менее 3-х лет	от 3-х до 5-ти лет
Срок Окупаемости	от 2-х до 5-ти лет	более 5-ти лет	менее 2-х лет
Масштаб внедрения	за рубежом	в своём регионе	в стране

• Х3.

№ 80

Проекты	Х1	Х2	Х3
Ожид.экон. эффективн.	Высокая	Низкая	Средняя
Срок выполнения	более 5-ти лет	менее 3-х лет	от 3-х до 5-ти лет
Срок Окупаемости	менее 2-х лет	более 5-ти лет	от 2-х до 5-ти лет
Масштаб внедрения	в своём регионе	за рубежом	в стране

• Х3.

Решение однокритериальных задач принятия решений в условиях риска.

№ 81
Магазин «Молоко» продает в розницу молочные продукты. Директор магазина должен определить, сколько бидонов сметаны следует закупить у производителя для торговли в течение недели. Вероятности того, что спрос на сметану в течение недели будет 7; 8; 9; 10 бидонов, равны соответственно 0,2; 0,2; 0,5; 0,1. Покупка одного бидона сметаны обходится магазину в 70 у.е., а продается сметана по цене 110 у.е. за бидон. Если сметана не продана в течение недели, она портится, и магазин несет убытки. Оцените наилучший вариант, используя критерий Байеса. Число закупаемых бидонов:
• (8)

№ 82
Главный инженер предприятия решает, строить или не строить новую производственную линию, использующую высокую технологию. Если новое оборудование заработает, компания будет получать прибыль $200000. Если не заработает, то компания получит убыток $150000. Главный инженер считает, что шансы на неуспех нового процесса — 60%. Величина дохода этого решения:
• (0)

№ 83
Президент компании решает, строить или нет промышленное предприятие. Его решения сведены в следующую таблицу.

Варианты	Строить большой завод	Строить малый завод	Ничего не делать	Вероятность
Благоприятный рынок, $	400000	80000	0	0,4
Неблагоприятный рынок, $	-300000	-10000	0	0,6

Величина дохода этого решения:
• (26000)

№ 84
Малый производитель ряда продуктов из сыра определяет, сколько ящиков сыра производить каждый месяц. Вероятность, что спрос будет 6 ящиков, равна 0.1, семь —0.3 и восемь —0.5, девять —0.1. Затраты на каждый ящик — $45. а цена — $95. В случае непродажи ящика к концу месяца он списывается как испорченный. Число производимых ящиков в каждый месяц:
• (8)

№ 85
Владелец бензоколонки думает о том, каков должен быть размер его станции. После полного анализа маркетинговых факторов, относящихся к производству бензина и спросу на него, он разработал следующую таблицу.

Размер станции	Маленькая	Средняя	Большая	Очень большая	Вероятность
Хороший рынок, $	50000	80000	100000	300000	0,2
Средний рынок, $	20000	30000	30000	25000	0,5
Плохой рынок, $	-10000	-20000	-40000	-160000	0,3

Величина дохода:
• (25000)

№ 86
Предприятие является малым поставщиком химикатов, используемых в фотографии. Один товар, поставляемый им,— это ВС-6. Менеджер обычно имеет запас 11, 12 или 13 ящиков ВС-6 на каждую неделю. За каждый проданный ящик полученная прибыль равна $35. Так как ВС-6 является реактивом с коротким сроком годности, то в случае непродажи его к концу недели менеджер должен его уничтожить. Он теряет $56 в каждом случае, когда что-то не продал в конце недели. Вероятность продажи 11 ящиков—0.45, 12 ящиков—0.35. и вероятность продажи 13 ящиков —0.2. Число ящиков, необходимых иметь в запасе каждую неделю:
• (11)

№ 87
Для финансирования проекта бизнесмену нужно занять сроком на один год 35000 ф. ст. Банк может одолжить ему эти деньги под 19% годовых или вложить в другое дело со 100%-ным возвратом суммы, но под 11% годовых. Из прошлого опыта банкиру известно, что 10% таких клиентов ссуду не возвращают, но сумма возмещения от заложенного имущества составит 25000 ф.ст. Величина чистого дохода:
• (4985)

№ 88
Промышленное предприятие может получать выключатели от двух поставщиков. Объем поставки 10000 выключателей. Качество выключателей от этих поставщиков показано ниже.

Процент дефектов	1	3	5
Вероятность для поставщика А	0,7	0,2	0,1
Вероятность для поставщика В	0,3	0,4	0,3

Неисправный выключатель может быть отремонтирован за $0.50. Хотя качество у поставщика В ниже, но он просит за 10000 выключателей на $37 меньше, чем поставщик А. На сколько долларов будет отличаться доход одного решения от другого?
• (97)

№ 89
В результате исследования рынка было признано, что существует 3 варианта развития Проекта.
По “оптимистическому” сценарию:
Приведенные результаты составят 50 тысяч евро;
Приведенные затраты – 5 тысяч евро;
Вероятность наступления сценария – 0,25
По “нормальному» сценарию”:
Приведенные результаты составят 30 тысяч евро;
Приведенные затраты – 15 тысяч евро;
Вероятность наступления сценария – 0,5
По “пессимистическому” сценарию:
Приведенные результаты составят 15 тысяч евро;
Приведенные затраты – 20 тысяч евро;
Вероятность наступления сценария – 0,25
Величина ожидаемой прибыли при варианте развития проекта, при использовании критерия Байеса.
• (17.5 тыс. евро)

№ 90
Фирма купила станок за 100 ден.ед. Для его ремонта можно купить специальное оборудование за 50 ден.ед. или обойтись старым. Если станок выходит из строя, его ремонт с помощью спецоборудования обойдется в 10 ед., без спецоборудования - 40 ед. Известно, что в течение срока эксплуатации станок выходит из строя не более 3 раз: вероятность того, что станок не сломается –0,3; сломается 1 раз – 0,4 раз; сломается 2 раза – 0,2; сломается 3 раза – 0,1. Определить целесообразность приобретения специализированного ремонтного оборудования. Величина суммарных затрат на покупку станка и его эксплуатацию при этом решении:
• (144)

Решение многокритериальных задач принятие решений в условиях риска и неопределенности.

№ 91
Перед ЛПР стоит задача транспортировки грузов от поставщиков к потребителям автомобильным транспортом либо по асфальтированной дороге (Х1), либо по грунтовой (Х2), либо по гравийной (Х3). На пути следования транспорта встречаются переправы через речки, таможенные посты, границы и т.п. В день отправки автомобилей возможно изменение погодных условий (е1 – сухая ясная погода; е2 – кратковременные дожди; е3 – сильные продолжительные дожди), а вмести с ними и транспортных расходов (ремонт, бензин и т.п.). При условии, что известны матрицы исходов по критерию «Время» (временные затраты в днях) перевозки грузов от поставщиков к потребителям в различных погодных условиях и распределение вероятностей появления состояний внешней среды (р1=0,2; р2=0,4; р3=0,4), следует определить наилучшую альтернативу транспортировки грузов с учетом двух (равнозначных) критериев. Нормировку критериев производить относительно их максимальных значений из таблицы исходов. Возможные исходы транспортировки грузов:

	Дорога	Х1	Х2	Х3
Критерий «Деньги» (в т.руб.)	е1	30	20	10
Критерий «Деньги» (в т.руб.)	е2	40	30	20
Критерий «Деньги» (в т.руб.)	е3	50	70	40
Критерий «Время» (в днях)	е1	4	3	3
Критерий «Время» (в днях)	е2	4	4	5
Критерий «Время» (в днях)	е3	5	5	7

Определите наилучшую альтернативу транспортировки грузов.
• Х3.

№ 92

	Дорога	Х1	Х2	Х3
Критерий «Деньги» (в т.руб.)	е1	10	20	10
Критерий «Деньги» (в т.руб.)	е2	40	30	30
Критерий «Деньги» (в т.руб.)	е3	50	70	60
Критерий «Время» (в днях)	е1	4	3	3
Критерий «Время» (в днях)	е2	4	4	5
Критерий «Время» (в днях)	е3	5	5	7

• Х1.

№ 93

	Дорога	Х1	Х2	Х3
Критерий «Деньги» (в т.руб.)	е1	30	20	10
Критерий «Деньги» (в т.руб.)	е2	40	30	30
Критерий «Деньги» (в т.руб.)	е3	60	70	60
Критерий «Время» (в днях)	е1	4	3	2
Критерий «Время» (в днях)	е2	4	4	5
Критерий «Время» (в днях)	е3	5	5	7

• Х2.

№ 94

	Дорога	Х1	Х2	Х3
Критерий «Деньги» (в т.руб.)	е1	40	30	20
Критерий «Деньги» (в т.руб.)	е2	40	40	50
Критерий «Деньги» (в т.руб.)	е3	50	50	70
Критерий «Время» (в днях)	е1	3	2	1
Критерий «Время» (в днях)	е2	4	3	3
Критерий «Время» (в днях)	е3	6	7	6

• Х2.

№ 95

	Дорога	Х1	Х2	Х3
Критерий «Деньги» (в т.руб.)	е1	40	30	30
Критерий «Деньги» (в т.руб.)	е2	40	40	50
Критерий «Деньги» (в т.руб.)	е3	50	50	70
Критерий «Время» (в днях)	е1	1	2	1
Критерий «Время» (в днях)	е2	4	3	3
Критерий «Время» (в днях)	е3	5	7	6

• Х1.

№ 96
Сотруднику фирмы предлагается пройти курс обучения в одном из центров повышения квалификации:
х1 – курсы с дневной формой обучения;
х2 – курсы по заочной форме обучения;
х3 – курсы по дистанционной форме обучения.
Выбор центра сотрудник производил по следующим критериям:
К1- продолжительность обучения (года);
К2- плата за обучение (т.руб в год);
К3- качество обучения (1-высокое, 2- среднее);
Предпочтения решений по каждому критерию сотрудник представил в виде матриц парных сравнений, в которых цифра 1 означает, что альтернатива по строке не уступает альтернативе по столбцу. Значимость критериев оценил соответственно 0,3; 0.5; 0,2.

Определить функцию принадлежности решений к множеству недоминируемых решений через нечеткие отношения предпочтений Q по формуле:
,
x∈X

Х1	(1)
Х2	(2)
Х3	(3)

• (0.4;0.6;1)

№ 99

,
x∈X

Х1	(1)
Х2	(2)
Х3	(3)

• (1;1;1)

№ 101

,
x∈X

Х1	(1)
Х2	(2)
Х3	(3)

• (1;1;0.6)

№ 102
- Значимость критериев соответственно 0,3; 0.2; 0,5.

,
x∈X

Х1	(1)
Х2	(2)
Х3	(3)

• (1;0.4;0.6)

№ 105
-
,
x∈X

Х1	(1)
Х2	(2)
Х3	(3)

• (1;0.4;1)

Решение однокритериальных задач принятие решений в условиях неопределенности.

№ 106
Магазин «Молоко» продает в розницу молочные продукты. Директор магазина должен определить, сколько бидонов сметаны следует закупить у производителя для торговли в течение недели: 7, 8, 9 или 10 бидонов. Покупка одного бидона сметаны обходится магазину в 70 у.е., а продается сметана по цене 110 у.е. за бидон. Если сметана не продана в течение недели, она портится, и магазин несет убытки. Оцените наилучший вариант, используя критерий Вальда (гарантированного результата). Число закупаемых бидонов:
• (7)

№ 107
- критерий Сэвиджа.
• (8)

№ 108
Малый производитель ряда продуктов из сыра определяет, сколько ящиков сыра производить каждый месяц: 6, 7, 8 или 9. Затраты на каждый ящик — $45. а цена — $95. В случае непродажи ящика к концу месяца он списывается как испорченный. Наилучший вариант, используя критерий Вальда. Число производимых ящиков в каждый месяц:
• (6)

№ 109
- критерий Сэвиджа.
• (8)

№ 110
Предприятие является малым поставщиком химикатов, используемых в фотографии. Один товар, поставляемый им,— это ВС-6. Менеджер обычно имеет запас 11, 12 или 13 ящиков ВС-6 на каждую неделю. За каждый проданный ящик полученная прибыль равна $35. Так как ВС-6 является реактивом с коротким сроком годности, то в случае непродажи его к концу недели менеджер должен его уничтожить. Он теряет $56 в каждом случае, когда что-то не продал в конце недели. Критерий Вальда. Число ящиков, необходимых иметь в запасе каждую неделю:
• (11)

№ 111
- критерий Сэвиджа.
• (12)

№ 112
Владелиц бензоколонки думает о том, каков должен быть размер его станции. К его большому сожалению, он не знает, каков будет рынок в обозримом будущем, но в предположении возможного развития рынка, он смог оценить доходы его бизнеса (см. таблицу):

Размер станции	Хороший рынок, $	Средний рынок, $	Плохой рынок, $
Маленькая	50000	20000	-10000
Средняя	80000	30000	-20000
Большая	100000	30000	-40000
Очень большая	300000	25000	-160000

Оцените наилучший вариант решения, используя критерий Бернулли-Лапласа. Величина дохода этого решения.
• (55000)

№ 113
- критерий Сэвиджа. Величина риска (потерь) этого решения.
• (150000)

№ 114
Фирма купила станок за 100 ден.ед. в надежде произвести в течении его срока эксплуатации изделия на общую сумму 1000 ден.ед. Для его ремонта можно купить специальное оборудование за 50 ден.ед. или обойтись старым. Если станок выходит из строя, его ремонт с помощью спецоборудования обойдется в 10 ед., без спецоборудования - 40 ед. Известно, что в течение срока эксплуатации станок может сломаться 1 раз; сломаться 2 раза; сломаться 3 раза и вообще не сломаться. Определить целесообразность приобретения специализированного ремонтного оборудования, используя критерий Бернулли-Лапласа. Величина суммарных затрат на покупку станка и его эксплуатацию.
• (160)

№ 115
- критерий Вальда. Величина гарантированного чистого дохода с учетом затрат на покупку станка и его эксплуатацию.
• (880)