
Структура и алгоритмы обработки данных в ЭВМ
Кафедра АСУ
Горитов А.Н.
Томск-2000
№ 1
Атрибут объекта - это:
• уникальный набор свойств.
№ 2
Наборы атрибутов различных объектов:
• могут пересекаться, но не могут совпадать.
№ 3
Экземпляр объекта описывается:
• конкретным набором значений атрибутов.
№ 4
Минимальная адресуемая единица памяти:
• байт.
№ 5
Минимальным полем фиксированной длины является:
• полуслово.
№ 6
Важнейший архитектурный признак ЭВМ:
• слово.
№ 7
Структуры, обладающие свойством “непредсказуемости размера структуры в процессе ее обработки”:
• полустатические структуры;
• динамические структуры.
№ 8
Структуры, обладающие свойством “отсутствие физической смежности элементов структуры в памяти ЭВМ”:
• полустатические структуры;
• динамические структуры.
№ 9
К динамическим структурам относятся:
• связанные списки.
№ 10
К статическим структурам относятся:
• массивы, записи, множества.
№ 11
К полустатическим структурам относятся:
• стеки, очереди, деки.
№ 12
Статические структуры отличаются от полустатических:
• постоянством структуры в течении всего времени ее существования;
• отсутствием информации об отношениях между элементами в самих элементах структуры.
№ 13
Тип Character предназначен для:
• хранения одного символа - буквы, знака или кода.
№ 14
Тип Boolean предназначен для:
• запоминания логического значения.
№ 15
Индексы массива:
• могут вычисляться.
№ 16
Представление строки в Turbo Pascale:
• длина строкового типа в байтах равна его максимальной строке плюс единица;
• первый байт содержит текущую длину строки, следующие - символы строки.
№ 17
Вариантная часть в записи:
• должна быть последней.
№ 18,19
Множество это:
• неупорядоченная совокупность элементов;
• произвольный набор однотипных объектов, понимаемых как единое целое.
№ 20
Базовым типом множества может быть:
• перечислимый и интервальный.
№ 21
Множеством - степенью называется:
• множества всех подмножеств.
№ 22
var p:set of 0..9; i, j: integer;
Если i=3 и j=5, то какое значение получит переменная p при выполнении следующего оператора присваивания - p := [2*i..j]:
• [ ].
№ 23
Чему равен результат [ 1, 3, 5 ] * [ 2, 4 ]:
• [ ].
№ 24
Вычислить значения отношений:
1) [ 2 ] <> [ 2, 2, 2 ];
2) [ 'a', 'b' ] = [ 'b', 'a' ];
3) [ 4, 5, 6 ] = [ 4..6 ];
4) [ 'c, 'b' ] = [ 'c'..'b' ];
5) [ 2, 3, 5, 7 ] <= [ 1..9 ]
6) [ 3, 6..8 ] <= [ 2..7, 9 ]
• (false true true false true false)
№ 25
1) [ ] <= [ '0'..'9']
2) 'q' in [ 'a'..'z' ]
3) trunc (3.9) in [ 1, 3, 5 ];
4) odd (4) in [ ];
5) [ 2 ] < [ 1..3 ];
6) 66 = [ 66 ].
• (true true true false ошибка ошибка)
№ 26
Основной метод, используемый при файловой сортировки:
• метод слияния.
№ 27
В последовательном файле доступ к элементам:
• доступен только один элемент, другие - только путем последовательного продвижения по файлу.
№ 28
В качестве базового типа файла может быть:
• простой или структурированный, но не файл .
№ 29
Под слиянием упорядоченных файлов понимают:
• объединение этих файлов в одну упорядоченную последовательность при помощи циклического выбора элементов, доступных в данный момент
№ 31
Фазой называется:
• операция, которая однократно обрабатывает всё множество данных.
№ 32
Наименьший подпроцесс, который, повторяясь, образует процесс сортировки - это:
• проход.
№ 33
Название метода?
Метод сортировки файлов, который состоит в следующем:
1) последовательность А разбивается на две половины В и С;
2) последовательности В и С сливаются при помощи объединения отдельных элементов в упорядоченные пары;
3) полученной последовательности присваивается имя А, после чего повторяются шаги 1) , 2), при этом упорядоченные пары сливаются в упорядоченные четверки;
4) предыдущие шаги повторяются при этом четверки сливаются в восьмерки и т. д.
• простым слиянием.
№ 34
Метод сортировки, при котором каждый раз сливаются две самые длинные возможные последовательности называется:
• метод естественного слияния.
№ 35
const n = 100;
var aa : array [ 1..n ] of tt;
t: integer;
где tt - любой тип.
Это определение:
• стека.
№ 36
const n = 100;
var aa : array [ 1..n ] of tt;
f, r : integer;
где tt - любой тип.
Это определение:
• очереди.
№ 37
Чему будет равен указатель на стек, если стек стал пустым, после извлечения из него всех элементов?
• нулю.
№ 38
Дек - это:
• сочетание очереди и стека.
№ 39
Неверная операцию для очереди:
• включение нового элемента перед элементом с номером k.
№ 40
Стек - это линейный последовательный список, в котором:
• включение элементов выполняется с одного конца, т.е. доступен только последний элемент.
№ 41
В вершине стека находится:
• последний по времени поступления элемент.
№ 42
Стек считается пустым если:
• вершина стека смещена вниз на длину одной ячейки относительно низа стека.
№ 43
В односвязном списке каждый элемент состоит из:
• содержательного поля и поля указателя.
№ 44
Неверное свойство связных списков:
• невозможно включить элемент в связный список в любое место списка.
№ 45
Свойство, присущее кольцевому связному списку:
• просмотр списка можно начинать с любого элемента.
№ 46
Данные типа Pointer:
• указывают на некоторые данные или группу данных.
№ 47
Область памяти, ранее занимаемая элементом динамической структуры после ее освобождения:
• может повторно использоваться для этой же динамической структуры.
№ 48
Элементы, выделяемые динамически:
• не имеют имени.
№ 49
type A = array [ 1..100 ] of integer;
PA = ^a;
Здесь значение переменной PA является:
• ссылка на динамический объект, значением которого является массив из 100 целых чисел.
№ 50
Пусть Р - указатель, определенный ранее. Тогда Р^ означает:
• сама переменная.
№ 51
Указатель определен как
VAR J : ^integer;
• переменная J может использоваться только для ссылки на элементы типа integer.
№ 52
После введения в употребление ссылочной переменной она: ссылается на программные объекты; имеет своим значение пустую ссылку Nil?
• не имеет ни того, ни другого.
№ 53
Пусть объявлена переменная - var p : T;
При выполнении операции new(p):
• выделяется память для переменной типа Т, а переменная указатель р получает значение ссылки на динамически размещенную переменную.
№ 54
После выполнения блока программы
var j : ^integer;
new (j);
j^ : 7;
j := Nil;
• указатель j никуда не указывает, но область остается занятой.
№ 55
Процедура dispose(p):
• освобождает область памяти, на которую указывает указатель p.
№ 56
Ошибка при выполнении процедуры dispose(p) не выдается в случае:
• если р имеет любое значение, кроме Nil.
№ 57
Что описывает ниже приведенный фрагмент программы
type a = ^b;
b = record
name : integer;
c : a;
end;
var ff : a;
• стек.
№ 58
Что выполняет ниже приведенная процедура:
type a = ^b;
b = record
name : integer;
c : a;
end;
var ff : a;
Procedure d( k : integer);
var w : a;
begin
new (w);
w^.name := k;
w^.c := ff;
end;
• размещает новый элемент в стеке.
№ 59
type a = ^b;
b = record
name : integer;
c : a;
end;
var ff : a;
Procedure m(var u : integer);
var L : a;
begin
L := ff;
u := L^.name;
a := L^.c;
dispose( L );
end;
• извлекает элемент из стека.
№ 60
Описание
a = ^b;
b = record
name : integer;
c : a;
end;
d = record
aa = a;
bb = a;
end;
var E : d
Это:
• описание очереди.
№ 61
a = ^b;
b = record
name : integer;
c : a;
end;
d = record
aa = a;
bb = a;
end;
var E : d
Function S (m : d): Boolean;
begin
if m.aa = Nil then
S := true else S:= false
end;
Эта функция:
• проверка наличия элементов в очереди.
№ 62
a = ^b;
b = record
name : integer;
c : a;
end;
d = record
aa = a;
bb = a;
end;
var E : d
Procedure asd( var m : d; st : integer);
var p : a;
begin
new(p);
p^.name := st;
p^.c := Nil;
if s(m) then
begin
m.aa := p;
m.tt := p end
else begin
m.bb^.c := p;
m.tt := p
end;
end;
Это процедура выполняет:
• размещение нового элемента в очереди.
№ 63
a = ^b;
b = record
name : integer;
c : a;
end;
d = record
aa = a;
bb = a;
end;
var E : d
Function k ( m: d ): integer;
begin
k := m.aa^.name;
end;
Это функция выполняет:
• извлечение значения объекта, стоящего в начале очереди.
№ 64
a = ^b;
b = record
name : integer;
c : a;
end;
d = record
aa = a;
bb = a;
end;
var E : d
Procedure n ( var m : d );
var w : a;
begin
w := m.aa;
m.aa := m.aa^.next;
dispose(w);
end;
Эта процедура выполняет:
• удаление старшего элемента из очереди.
№ 65
Элемент в дереве, на который не ссылается ни какой другой элемент:
• корень.
№ 66
Элемент в дереве, на который могут ссылаться другие элементы, и он в свою очередь может ссылаться на несколько элементов следующего уровня иерархии:
• узел.
№ 67
Иерархическая структура, каждый элемент промежуточного уровня которого порожден только одним элементом более высокого уровня:
• дерево.
№ 68
Элементы дерева, которые не ссылаются на другие элементы:
• лист.
№ 69
Связь между элементами предыдущего уровня и последующего уровня в дереве:
• предок - потомок.
№ 70
“Вырожденным деревом” называют:
• список.
№ 71
Любое дерево нельзя описать:
• списками.
№ 72
Высотой дерева называется:
• максимальный уровень дерева.
№ 73
Степень дерева называется:
• максимальная степень всех узлов дерева.
№ 74
Длиной пути к вершине x называется:
• число ветвей или ребер, которые нужно пройти от корня к вершине x.
№ 75
Длина пути дерева - это:
• сумма длин путей всех его узлов.
№ 76
Бинарное дерево - это:
• дерево второй степени.
№ 77
Дано двоичное дерево.
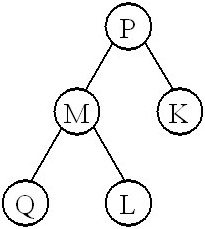
В какой последовательности выполняется обход вершин в случае:
обхода сверху вниз;
обхода слева направо;
обхода снизу вверх.
В ответе последовательность вершин для каждого обхода соответственно.
• (PMQLK, QMLPK, QLMKP)
№ 78
Обход сверху вниз. Вид записи:
• префиксная.
№ 79
Обход слева направо.
• инфиксная.
№ 80
Обход дерева снизу вверх:
• постфиксная.
№ 81
Последовательный поиск в массиве:
• работает как для упорядоченных так и для неупорядоченных массивов.
№ 82
Двоичный поиск в массиве:
• работает для упорядоченных массивов.
№ 83
Из N элементов организуется двоичное дерево. Его высота:
• log2N.
№ 84
Практическое использование сильно ветвящихся деревьев:
• формирование и использование крупномасштабных деревьев поиска.
№ 85
Страница в сильно ветвящемся дереве это:
• поддерево.
№ 86
Б-дерево - это:
• совокупность страниц, сформированных особым образом.
№ 87
Неверное свойство Б-деревьев:
• листья могут располагаться на различных уровнях.
№ 88
Б-дерево растет:
• от листьев к корню.
№ 90
Дано дерево:
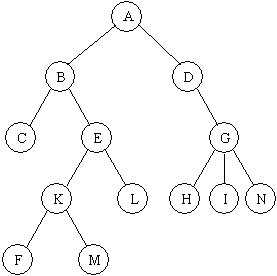
Сколько в дереве листьев?
• (7)
№ 91
- Сколько в дереве внутренних узлов?
• (5)
№ 92
- Длина путь до вершины M?
• (4)
№ 93
- Какова длина дерева?
• (31)
№ 94
- Разложить на вложенные скобки:
• [(A(B(C),E(K(F,M),L)),D(G(H,I,N))))]
№ 95
Даны два дерева:
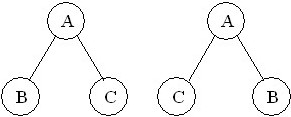
• они разные.
№ 96
Идеально-сбалансированное дерево это:
• все узлы расположены поровну слева и справа от каждого узла.
№ 99
Основное преимущество матрицы смежности:
• за один шаг можно ответить на вопрос существует ли ребро из x в y.
№ 100
Сколько ячеек памяти необходимо для представления графа с помощью списков инциденции (n - количество вершин, m - количество ребер):
• 2 x n x m.
№ 101
Рассмотрим следующий метод. Начинаем поиск с некоторой фиксированной вершины v0. Затем выбираем произвольную вершину u, смежную с v0 и повторяем наш просмотр от u. В общем случае предположим, что мы находимся в некоторой вершине v. Если существует новая (еще не просмотренная) вершина u, u-v, то мы рассматриваем эту вершину. (она перестает быть новой) начиная с нее, продолжаем поиск. Если же не существует новой вершины, смежной с v, мы говорим, что вершина v использована, возвращаемся в вершину, из которой попали в v и продолжаем поиск (если v=v0, то поиск закончен). Этот метод называется:
• поиск в ширину в графе.
№ 102
Произвольный путь, проходящий через каждое ребро графа ровно один раз, называется:
• Эйлеровым путем.
№ 103
Условие существования гамильтонова пути:
• граф должен быть связан и должен содержать не более чем две вершины нечетной степени.
№ 104
Путь, проходящий ровно один раз через каждую вершину:
• гамильтонов путь.
№ 105
В процессе вычисления расстояния от одной вершины a до другой вершины b в графе мы находим:
• расстояние от a до всех вершин графа.
№ 106
Алгоритм Дейкстры справедлив для графов, у которых:
• веса всех дуг неотрицательны.
№ 107
Критический путь в графе называется:
• максимальный по длине путь из a в b.
№ 108
Какой метод используется при отыскании фундаментального множества циклов:
• метод поиска в глубину.
№ 109
Гамильтонов путь?
• обход графа с проходом по всем узлам графа по одному разу.
№ 110
Алгоритмы с возвратом используются:
• при построении гамильтонова пути графа.
№ 111
С помощью какого из алгоритмов можно найти минимальный путь от исходной вершины X до произвольной вершины Y связанного графа:
• поиск в ширину.
№ 112
Вычислительная сложность алгоритма построения стягивающего дерева, использующего метод поиска в ширину:
• O(n+m).
№ 113
Вычислительная сложность общего алгоритма поиска кратчайшего пути от фиксированной вершины:
• O(n*m).
№ 114
Вычислительная сложность алгоритма Дейкстры нахождения кратчайшего пути:
• O (m log n).
| на главную | база по специальностям | база по дисциплинам | статьи |
Другие статьи по теме
