Сопротивление материалов
Кемеровский технологический институт пищевой промышленности
Яремчук А.И.
Томск-2003

№ 1
“Сопротивление материалов” решает задачи:
• на прочность, жесткость и устойчивость.

№ 2
Классификация внешней нагрузки по характеру приложения:
• сосредоточенная, распределенная и объемная нагрузки.

№ 3
- по характеру изменения во времени:
• статические, повторные и динамические.

№ 4
Конструкции подразделяются на элементы:
• стержень, оболочка, массив.

№ 5
Разновидностью стержня является элемент конструкции:
• брус.

№ 6
- разновидностью оболочки:
• пластина.

№ 7
Внутренние усилия в элементах конструкций определяются с помощью:
• метода сечений.

№ 8
Поперечная или перерезывающая сила и единицы измерения их в международной системе исчисления обозначаются буквой:
• Q, Н.

№ 9
- продольная сила:
• N, H.

№ 10
- крутящий момент:
• Mz; H*м.

№ 11
- изгибающиеся моменты:
• Mx и My, H*м.

№ 12
Величина полного напряжения в данной точке поперечного сечения:
• .

№ 13
Единицы измерения напряжения:
• Па.

№ 14
Величина в 1 Па:
• 1 ПА=1Н/1м².

№ 15
Полное напряжение раскладывается на?
• касательное и нормальное напряжения.

№ 16
Название и обозначение напряжения, лежащего в плоскости поперечного сечения:
• касательное, τ.

№ 17
- напряжение перпендикулярное плоскости поперечного сечения:
• нормальное, σ.

№ 18
Экспериментально, при механических испытаниях материалов в условиях линейного нагружения, определяют:
• предельное напряжение.

№ 19
Как некоторая доля от соответствующего предельного напряжения этого материала, назначается:
• допускаемое напряжение.

№ 20
Закон Гука:
• ε=σ/E.

№ 21
Величина коэффициента Пуассона:
• μ=|ε´/ε|.

№ 22
Относительное удлинение стержня:
• ε=Δl/A.

№ 23
Величина относительной поперечной деформации:
• ε´=ΔB/B.

№ 24
Абсолютное линейное удлинение (укорочение) отдельного участка бруса при растяжении или сжатии:
• Δl=(N*l)/(E*A).

№ 25
Полная линейная деформация стержня, состоящая из нескольких участков:
• .

№ 26
Жесткость площади поперечного сечения стержня при растяжении или сжатии:
• E*A.

№ 27
Нормальное напряжение при растяжении или сжатии:
• σ=N/A.

№ 28
Условие прочности при растяжении и сжатии:
• σ_max=N/A ≤ [σ].

№ 29
Величина площади поперечного сечения стержня из условия прочности:
• A ≥ N/[sigma].

№ 30
Скачок на эпюре продольных сил равен:
• величине приложенной силы.

№ 31
Перемещение в точке заделки центрально-сжатого стержня равно:
• 0.

№ 32
Для плоской системы можно составить:
• 3 уравнения статического равновесия.

№ 33
- для пространственной системы:
• 6 уравнений.

№ 34
При растяжении или сжатии симметричных стержней возникают внутренние силовые факторы:
• продольные силы - N; нормальные напряжения - σ.

№ 35
Уравнение совместности перемещений для один раз статически неопределимых стержней при растяжении и сжатии:
• δ^F+δ^R=0.

№ 36
Уравнение по определению степени статической неопределимости:
• с.с.н. = n-х.

№ 37
Число неизвестных внутренних усилий в уравнении по определению степени статической неопределимости обозначается буквой:
• n.

№ 38
Число уравнений статического равновесия в уравнении по определению степени статической неопределимости:
• x.

№ 39
Величина перемещения точки заделки от действия внешних сил в статически неопределимых системах уравнения совместности перемещений при растяжении и сжатии:
• δ^F.

№ 40
Величина перемещения точки заделки от действия силы реакции в статически неопределимых системах уравнения совместности перемещений при растяжении и сжатии:
• δ^R.

 

№ 41
Стержень, работающий на кручение -
• вал.

№ 42
Отрезок вала, находящийся между двумя скручивающими моментами -
• участок.

№ 43
Величина касательного напряжения:
• τ=M_кр/W_ρ.

№ 44
Обозначение полярного момента сопротивления сечения:
• W_ρ.

№ 45
Полярный момент сопротивления площади поперечного сечения для круга:
• W_ρ=πd³/16 ≈ 0,2d³.

№ 46
Условие прочности при кручении:
• τ_max=M_кр/W_ρ ≤ [τ].

№ 47
Диаметр вала из условия прочности при кручении:
• .

№ 48
Скачок на эпюре крутящих моментов равен:
• скручивающему моменту.

№ 49
Угла сдвига при кручении:
• γ=τ/G.

№ 50
Обозначение модуля сдвига:
• G.

№ 51
Угл закручивания для участка вала:
• θ=(M_кр*l)/(E*J_ρ).

№ 52
Жесткость площади поперечного сечения вала:
• G*J_ρ.

№ 53
Относительный угол закручивания:
• φ1=M_кр/(G*J_ρ).

№ 54
Условие жесткости:
• φ1_max=(M_кр/G*J_ρ) ≤ [φ1].

№ 55
Полярный момент инерции площади поперечного сечения вала:
• J_ρ=πd⁴/32 ≈ 0,1d⁴.

№ 56
Диаметр вала из условия жесткости:
• .

№ 57
Сколько уравнений статического равновесия и какое можно записать для вала, загруженного внешними скручивающими моментами и защемленным с обоих концов?
• одно, .

№ 58
С помощью какого уравнения решается один раз статически неопределимая задача при кручении?
• уравнения совместности перемещений.

№ 59
Уравнение совместности перемещений при решении статически неопределимой задачи:
• θ_A^T+θ_A^MA=0.

№ 60
Угол закручивания в точке заделки вала:
• θ=0.

 

№ 61
Геометрическая характеристика - статический момент сечения фигуры относительно какой-либо оси х:
• .

№ 62
Расстояние от центра тяжести фигуры до оси х обозначается:
• y_C.

№ 63
Статический момент сечения фигуры относительно какой-либо оси у:
• .

№ 64
Расстояние от центра тяжести фигуры до оси y:
• x_c.

№ 65
Ордината центра тяжести составного сечения:
• .

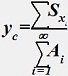№ 66
Абсцисса:
• .

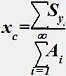№ 67
Осевой момент инерции сечения относительно оси x:
• .

№ 68
- относительно оси y?
• .

№ 69
Полярный момент инерции сечения:
• .

№ 70
- центробежный момент:
• .

№ 71
Центробежный момент инерции сечения J_xy, симметричного относительно какой-либо собственной оси инерции:
• 0.

№ 72
Момент инерции фигуры относительно какой-либо новой оси X₁, если известно, что расстояние от ее центральной оси X₀ до новой равно а:
• J_x1=J_x0+a²*A.

№ 73
y₁, y₀, b:
• J_y1=J_y0+b²*A.

№ 74
x₁ и y₁, x₀ и y₀, а и b?
• J_x1y1=J_x0y0+a*b*A.

№ 75
Осевые моменты инерции J_x и J_y прямоугольника при высоте h и ширине основания b:
• J_x=bh³/12, J_y=hb³/12.

№ 76
J_x и J_y прямоугольного треугольника:
• J_x=bh³/36, J_y=hb³/36.

№ 77
Угол поворота главных центральных осей U и V сечения относительно его центральных осей x₀ и y₀:
• .

№ 78
Максимальный главный момент инерции сечения:
•.

№ 79
Минимальный главный момент инерции сечения:
• .

№ 80
Центробежный момент инерции J_uν составного сечения относительно главных осей равен:
• 0.

 

№ 81
При изгибе возникают внутренние усилия:
• изгибающие моменты и поперечные силы.

№ 82
Стержень, работающий на изгиб -
• балка.

№ 83
Балка жестко закрепленная с одной стороны -
• консоль.

№ 84
Слой балки, в котором не возникают при изгибе деформации -
• нейтральный.

№ 85
Изгиб, если в поперечных сечениях балки возникает только внутренний изгибающий момент -
• чистый.

№ 86
При изгибе определяется численно как алгебраическая сумма всех активных и реактивных сил, взятых по одну сторону от сечения:
• поперечная сила.

№ 87
- как алгебраическая сумма моментов от всех активных и реактивных сил, взятых по одну сторону от этого сечения:
• изгибающий момент.

№ 88
Правило знаков для поперечных сил:

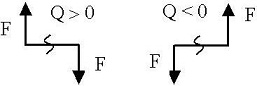
№ 89
Правило знаков для изгибающих моментов:

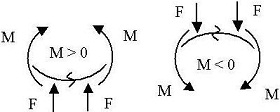
№ 90
Дифференциальная зависимость между изгибающим моментом и поперечной силой на длине участка балки:
• .

№ 91
- между поперечной силой и распределенной нагрузкой, действующей по длине участка балки:
• .

№ 92
Скачок на эпюре поперечных моментов при изгибе балки равен:
• сосредоточенной силе.

№ 93
- на эпюре изгибающих моментов:
• сосредоточенному моменту.

№ 94
Условие прочности по нормальным напряжениям при изгибе:
• .

№ 95
Момент сопротивления относительно оси х площади поперечного сечения балки и его единицы измерения в международной системе исчисления:
• W_x; M³.

№ 96
Прогиб при изгибе с помощью интеграла Мора:
• δ=∫₀¹(M_FM⁰*dx)/(EJ_x).

№ 97
- с помощью графоаналитического метода Верещагина:
• δ = (∑(ω_MF*M_c⁰) / EJ_x.

№ 98
Площадь эпюры изгибающего момента от внешних нагрузок при вычислении графоаналитического метода Верещагина:
• ω_MF.

№ 99
Ордината на эпюре изгибающих моментов, от единичной силы, находящейся под центром тяжести площади эпюры изгибающих моментов от внешних нагрузок:
• M_c⁰.

№ 100
Какая сила прикладывается в точке определения прогиба при вычислении графоаналитическим методом Верещагина?
• F₁=1.

 

№ 101
Одно из трех главных напряжений при котором возникает плоское напряженное состояние равно:
• 0.

№ 102
Для определения нормальных и касательных напряжений в наклонных площадках при плоском напряженном состоянии применяется:
• метод независимости действия сил.

№ 103
Максимальное главное напряжение при плоском напряженном состоянии:
• .

№ 104
- минимальное главное напряжение:
• .

№ 105
Максимальная величина касательного напряжения:
• .

№ 106
Величина относительной деформации в направлении оси х при объемном напряженном состоянии:
• ε_x=1/E*[σ_x-μ*(σ_y+σ_z)].

№ 107
- в направлении оси y:
• ε_y=1/E*[σ_y-μ*(σ_x+σ_z)].

№ 108
- в направлении оси z:
• ε_z=1/E*[σ_z-μ*(σ_x+σ_y)].

№ 109
Объемная относительная деформация при объемном напряженном состоянии:
• ε_ν=ε_x+ε_y+ε_z.

№ 110
Удельная потенциальная энергия формоизменения:
• .

№ 111
Вид деформации, который возникает, если продольная нагрузка приложена с некоторым эксцентриситетом относительно центра тяжести поперечного сечения стержня -
• внецентренное растяжение (сжатие).

№ 112
Напряжение в любой точке поперечного сечения стержня при внецентренном растяжении:
• .

№ 113
- при внецентренном сжатии:
• .

№ 114
Линия, делящая сечение стержня на две площади с противоположными по знаку напряжениями, при внецентренном растяжении или сжатии, называется:
• нулевая.

№ 115
Уравнение нулевой линии в виде уравнения прямой в отрезках:
• (x₀/a)+(y₀/b)=1.

№ 116
Отрезок (а), отсекаемый нулевой линией на оси х при внецентренном сжатии:
• a = -i_y² / x_F.

№ 117
- отрезок (b), на оси y площади поперечного сечения стержня:
• b = -i_x² / y_F.

№ 118
Величины радиусов инерции площади поперечного сечения относительно осей х и y:
• i_x=√(J_x/A), i_y=√(J_y/A).

№ 119
Условие прочности по растягивающим напряжениям при внецентренном растяжении стержня:
• σ_max=(N/A)+(M_x/W_x)+(M_y/W_y) ≤ [σ_ρ].

№ 120
- по сжимающим напряжениям:
• σ_max=-(N/A)-(M_x/W_x)-(M_y/W_y) ≤ [σ_СЖ].

 

№ 121
Условие прочности по третьей гипотезе прочности (гипотезе наибольших касательных напряжений) через главные напряжения:
• σ_ЭКВ=σ₁-σ₃ ≤ [σ].

№ 122
Величина эквивалентного момента по третьей теории прочности при совместном действии кручения и изгиба:
• M_ЭКВ = √(∑M_из² + M_КР²).

№ 123
- по четвертой теории:
• M_ЭКВ = √(∑M_из² + 0,75 M_КР²).

№ 124
Суммарный изгибающий момент:
• M_из=√(M_x² + M_y²).

№ 125
Осевой момент сопротивления сечения относительно оси х площади поперечного сечения вала:
• W_x = πd³/32 ≈ 0,1d³.

№ 126
Диаметр вала, из условия прочности при совместном действии кручения и изгиба:
• d ≥ √(M_ЭКВ/0,1[σ]).

№ 127
Величина скручивающего момента (Н*м), передаваемого на вал, если мощность N в лошадиных силах, а число оборотов n в об/мин:
• M_K=7162 N/n.

№ 128
N в кВт, n в об/мин:
• M_K=9736 N/n.

№ 129
N в кВт, #math omega в рад/с:
• M_K=N/ω.

№ 130
Зависимость, использующаяся для подбора сечений при совместном действии кручения и изгиба:
• .

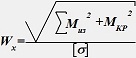№ 131
Для определения давления на вал в местах крепления шкивов от действия суммарных сил натяжения ветвей при кручении и изгибе применяют:
• метод приведения сил.

№ 132
Натяжение ветви t на шкиву с диаметром D:
• t=2M_К/D.

№ 133
Касательные напряжения от действия изгиба, при расчете на кручение с изгибом, не учитываются, так как:
• τ во много раз меньше σ.

№ 134
Четвертая гипотеза прочности для плоского напряженного состояния через главные напряжения:
• σ_ЭКВ=√(σ₁²+σ₃²-σ₁σ₃) ≤ [σ].

№ 135
- через нормальные σ и касательные напряжения τ:
• σ_ЭКВ=√(σ²+3τ²) ≤ [σ].

№ 136
Осевые моменты сопротивления сечения прямоугольника высотой h и шириной основания b:
• W_x=bh²/6, #l(W,y)=bh²/6.

№ 137
Какие точки площади поперечного сечения вала будут являться опасными при расчете на кручение и изгиб?
• окружность.

№ 138
Место вала, где наибольшее значение эквивалентного момента -
• опасное сечение.

№ 139
Единицы измерения стандартные величины диаметров валов -?
• мм.

№ 140
Зависимость между полярным и осевым моментами сопротивления плоского сечения для круга:
• W_ρ=2W_x.

 

№ 141
Формы равновесия:
• устойчивая, безразличная, неустойчивая.

№ 142
Сила, при наименьшем значении которой стержень теряет устойчивую форму равновесия:
• критическая сила F_кр.

№ 143
Значение сжимающей продольной силы F, по сравнению с критической силой F_кр., при которой стержень будет сохранять устойчивую форму равновесия:
• F<F_кр.

№ 144
- будет иметь безразличную форму:
• F=F_кр.

№ 145
- будет находиться в неустойчивой форме:
• F>F_кр.

№ 146
Критическая сила по формуле Эйлера:
• F_кр = (π²*E*J_min) / (μ*l)².

№ 147
Формула Эйлера применима при:
• λ ≥ λ_пред..

№ 148
Коэффициент приведения длины, зависящий от способа закрепления стержня, и величины этого коэффициента:
• μ; 2, 1, 0,75; 0,5.

№ 149
Гибкость стержня:
• λ = μ*l / i_min.

№ 150
Предельная гибкость стержня при продольном сжатии:
• l_пред.=√(π²E/σ_пред).

№ 151
Минимальный радиус инерции площади поперечного сечения стержня:
• i_min=√(j_min/A).

№ 152
Критическая сила по формуле Ясинского:
• F_кр.=A(a-bλ).

№ 153
Формула Ясинского, для определения критической силы при продольном изгибе, применима при:
• #math λ<λ_пред..

№ 154
Буквы а и b в формуле Ясинского для определения критической силы обозначают:
• эмпирические коэффициенты.

№ 155
Величины эмпирических коэффициентов:
• а=310 МПа; b=1,14 МПа.

№ 156
Допускаемая нагрузка [F], действующая на сжатый стержень, после определения критической силы F_кр:
• [F]=F_КР/n_y.

№ 157
Допускаемая нагрузка при любой гибкости продольно сжатого стержня:
• [F]=θ*[σ_C]*A.

№ 158
Коэффициент продольного изгиба θ зависит от:
• материала и гибкости.

№ 159
Предел измерения θ:
• 0÷1.

№ 160
Площадь поперечного сечения стержня при расчете на устойчивость:
• A=[F]/θ*[σ_C].

 

№ 161
Недостаточно для определения внутренних усилий уравнений статического равновесия:
• статически неопределимым системам.

№ 162,163
Степень статической неопределимости плоских рам:
• С = Х - 3, где “Х” - число неизвестных связей, “3” - число уравнений статики для плоской системы.

№ 164
Статическую неопределимость плоской рамы позволяет раскрыть:
• метод сил.

№ 165
Рама с отброшенными лишними связями и внешними нагрузками, остающаяся геометрически неизменяемой и статически определимой, называется:
• основной системой - ОС.

№ 166
Рама с заданными внешними нагрузками, а в направлении отброшенных связей приложены пока неизвестные усилия, называется:
• эквивалентной системой - ЭС.

№ 167
Неизвестные усилия эквивалентной системы определяются из:
• канонических уравнений метода сил.

№ 168
Физический смысл канонических уравнений метода сил:
• перемещение точки приложения неизвестных сил, в эквивалентной системе, по направлению этих неизвестных сил, вызванное действие всех сил равно нулю.

№ 169
Общий вид канонических уравнений для n раз статически неопределимой системы:
• δ₁₁*x₂+δ₁₂*x₂+δ₁₃*x₃+...+δ_1n*x_n+Δ_1F=0;
δ₂₁*x₂+δ₂₂*x₂+δ₂₃*x₃+...+δ_2n*x_n+Δ_2F=0;
--------------------------------------------
δ_n1*x₁+δ_n2*x₂+δ_n3*x₃+...+δ_nn*x_n+Δ_nF=0.

№ 170
В первом уравнении перемещение точки приложения первого лишнего неизвестного по его направлению от действия единичного значения этого неизвестного, обозначается:
• δ₁₁.

№ 171
В первом каноническом уравнении метода сил перемещение точки приложения первой неизвестной величины по ее направлению, вызванное истинным значением этой силы, обозначается:
• δ_{1 1}*x₁.

№ 172
В каноническом уравнении перемещение точки приложения первой неизвестной силы по ее направлению от действия внешних нагрузок, обозначается.
• Δ_1F.

№ 173,174,175
Коэффициенты канонического уравнения по способу Верещагина:
• .
• .
• .

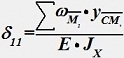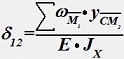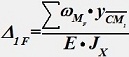№ 176
Площадь вогнутого параболического треугольника высотой “h” и шириной основания “b”:
• A=(1/3)b*h.

№ 177
- площадь выпуклого параболического треугольника:
• A=(2/3)b*h.

№ 178
Жесткое соединение в раме двух и более стержней называется:
• узлом.

№ 179
Проверка правильности построения окончательных эпюр внутренних усилий в точке узла рамы производится по уравнениям:
• ∑M=0; ∑X=0; ∑Y=0.

№ 180
В правильности построения окончательной эпюры изгибающих моментов от действия приложенных внешних нагрузок и найденных неизвестных усилий, убеждаются:
• деформационной проверкой.

 

№ 181
Характеры изменения напряжений:
• неустановившийся, установившийся, циклический.

№ 182
Однократная смена напряжений от наименьшего к наибольшему и обратно -
• цикл.

№ 183,184
Обозначения наибольшего и наименьшего по абсолютной величине напряжения цикла:
• P_max, P_min.

№ 185
Коэффициент ассиметрии цикла:
• r=p_min/p_max.

№ 186
Пределы величины коэффициента ассиметрии цикла:
• -1 ≤ r ≤ 1.

№ 187
Постоянная составляющая цикла:
• P_m = (P_max+ P_min) / 2.

№ 188
Коэффициент ассиметрии цикла при симметричном цикле изменения напряжений:
• r = -1.

№ 189
Небольшая величина периодически меняющегося напряжения, которой материал может противостоять практически долго без появления трещин усталости, называется:
• предел выносливости Pr.

№ 190
Условие прочности при циклических характерах изменения напряжений:
• P^D_max ≤ P_r/K_r.

№ 191
Круговая частота свободных колебаний #math omega системы с одной степенью свободы:
• ω=√(c/m).

№ 192
Коэффициент затухания колебаний:
• e=a/2m.

№ 193
При сильном нарастании величин амплитуд круговой частоты вынужденных колебаний φ1 и круговой частоты свободных колебаний ω, при стремлении φ1 → ω, наступит:
• явление резонанса.

№ 194
Работа падающего тела грузом Q с высоты H:
• W=Q(H+Δl_дин).

№ 195
Потенциальная энергия деформации при сжатии стержня:
• U=(Δl_дин*E*A)/2l.

№ 196
Динамическая деформация и величина напряжения при ударе грузом Q с высоты H неподвижного стержня:
• Δl_дин=Δl_cm*K_дин, σ_дин=σ_cm*K_дин.

№ 197
Динамический коэффициент при ударе в общем виде:
• K_дин=1+√(1+2H/Δl_cm).

№ 198
Величина деформации и напряжения при ударе, если произведено внезапное приложение нагрузки, т.е. H = 0:
• Δl_дин=2Δl_cm, σ_дин=2σ_cm.

№ 199
Динамический коэффициент, если соотношение двойной высоты падения к статической деформации более или равно 10:
• K_дин=√(1+2H/Δl_cm).

№ 200
Динамический коэффициент, если 2H/Δl_cm>110:
• K_дин=√(2H/Δl_cm).