
Cпецкурс-2
(Синергетика для программистов)
для специальности 220400
Кафедра АСУ
Зюзьков В.М.
Томск-2003
№ 1,2
Пусть f : R→R отображения на множестве вещественных чисел, определяемых законами:
1. f(x)=x+1
2. f(x)=x²+x+1
3. f(x)=sin(x+1)
4. f(x)=1
5. f(x)=x²-x+1
6. f(x)=cos(x+1)
Рассмотрим соответствующие одномерные дискретные динамические системы (R,f). Имеют неподвижную точку системы:
• (3,4,6)
№ 3
Пусть f : R→R отображение на множестве вещественных чисел, определяемое законом f(x)=0.5x+1. Одномерная дискретная динамическая система (R,f) имеет неподвижную точку:
• 2
№ 4
Определяемое законом f(x)=2x–10. Неподвижная точка:
• 10
№ 5
f(x)=x²+x+1.
• Неподвижных точек нет.
№ 6
f(x)=x²+x–1.
• Две неподвижных точки.
№ 7
f(x)=x²+x.
• Одна неподвижная точка.
№ 8
f(x)=sin(x).
• Неподвижных точек бесконечно.
№ 9
f(x)=max(x,10).
• Неподвижных точек бесконечно.
№ 10
Пусть f : N→N отображение на множестве целых положительных чисел, определяемое законом f(n)=min(n,10). Одномерная дискретная динамическая система (R,f).
• Количество неподвижных точек конечно и больше двух.
№ 11
Если при любых начальных условиях x0 из некоторой области при достаточно больших временах фазовая точка окажется сколь угодно близко к фазовой траектории A, то такая фазовая траектория называется аттрактором и является исключительной.
№ 12
Множество Ω всех начальных состояний {x0}, определяющих фазовые траектории, асимптотически притягивающихся к данному аттрактору A, называется бассейном этого аттрактора.
№ 13
Логистическое отображение f : x→λx(1-x) при некоторых 0<λ≤4 показывает хаотическое поведение. Значение λ:
• 4.
№ 14
Эволюция регулярного (нехаотического) движения, при котором с изменением управляющего параметра происходит бесконечная последовательность удвоения периода, приводящая к возникновению хаотического движения, называется сценарием ....
• Фейгенбаума.
№ 15
Рассмотрим динамическую систему (X, f), где на X задано расстояние d. Будем называть отображение f : X→X хаотическим, если выполняются следующие условия:
• f транзитивно;
• f биективно.
№ 16
Первым обнаружил странный аттрактор:
• Лоренц.
№ 17
Длина классического канторова множества, определенного на отрезке [0, 1]:
• 0.
№ 18
Пусть I - конечный замкнутый или бесконечный интервал в R. Если непрерывное отображение I→I имеет цикл периода 4, то оно имеет также и:
• цикл периода 2;
• неподвижную точку.
№ 19
Цикл периода 6:
1) циклы каждого четного периода m такого, что m > 4;
2) цикл периода 2;
3) неподвижную точку.
№ 20
Цикл периода 5:
• циклы каждого четного периода m такого, что m > 4;
• неподвижную точку.
№ 21
Цикл периода 3, то оно имеет также и цикл любого периода.
№ 22,23,24
Пусть dim обозначает топологическую размерность, dimH – размерность Хаусдорфа, dimM – размерность Минковского.
• Для всех множеств в евклидовом пространстве выполняется соотношение: dim X≤dimH X≤dimM X.
• Для всех фракталов: dim X<dimH X≤dimM X.
• Для всех самоподобных фракталов: dim X<dimH X=dimM X.
№ 25,26,27,28
• Классическое канторово множество на единичном отрезке имеет фрактальную размерность между 0 и 1.
• Снежинка Коха - между 1 и 2.
• Салфетка Серпинского - между 1 и 2.
• График нигде не дифференцируемой функции - между 1 и 2.
№ 29
• График функции Вейерштрасса является фракталом.
№ 30
• Линейное отображение в евклидовом пространстве переводит треугольники в треугольники.
• Частным случаем линейного отображения в евклидовом пространстве является подобие.
№ 31
• Детерминированный и рандомизированный алгоритмы позволяют построить аттрактор системы итерированных функций.
№ 32
Пространство K непустых компактов из Rn можно сделать метрическим, это позволит нам говорить о сходимости последовательности множеств при изучении ifs-систем. Определяемое расстояние называется
• расстоянием Хаусдорфа.
№ 33
Каждая система итерированных функций порождает предельное множество.
• Это предельное множество является единственным аттрактором.
• Это предельное множество можно получить с помощью рандомизированного алгоритма.
№ 34
В общем случае для построения системы итерированных функций вводится множество сжимающих отображений {Fi, коэффициент сжатия si < 1}, 1≤i≤m, действующих на Rn. Эти m отображений используются для построения одного сжимающего отображения F в пространстве K всех непустых компактов из Rn.
№ 35
Этот привлекательный способ сжатия изображения заключается в том, что исходное изображение разбивают на компоненты и считают их аттракторами некоторых систем итерированных функций. Такой метод называется
• фрактальное сжатие.
№ 36
Теорема. Предположим, что |c|<2. Пусть z∈C и пусть zn=fcn(z) для n = 1,2,3, ... . Если существует такое n0, что |zn0)|≥.., то имеет место ![]() , то есть орбита {fn(z)}n=1∞ стремится к бесконечности и z не принадлежит множеству Жюлиа J(fc).
, то есть орбита {fn(z)}n=1∞ стремится к бесконечности и z не принадлежит множеству Жюлиа J(fc).
• (2)
№ 37,38
• Отображение fc:C→C, fc(z)=z2+c, ведет себя хаотично на своем множестве Жюлиа.
№ 39
Пусть M - множество Мандельброта.
• Для каждой точки c∈M соответствующее ей множество Жюлиа J(fc) связно.
№ 40
• Граница множества Мандельброта является фракталом.
• Хаусдорфова размерность границы множества Мандельброта между 1 и 2.
№ 41
• Фрактал – это множество, у которого размерность Хаусдорфа больше топологической размерности.
№ 42
Клеточные автоматы были введены в конце 40-х годов
• Станиславом Уламом и Джоном фон Нейманом.
№ 43
Клеточный автомат можно рассматривать как альтернативу традиционным математическим методам при моделировании природных явлений. Модель, описываемая с помощью системы дифференциальных уравнений в частных производных, во многих случаях может быть заменена моделью с клеточным автоматом.
№ 44,45
Исследуя клеточные автоматы, С. Вольфрам выяснил, что эволюция одномерных клеточных автоматов может быть отнесена к одному из следующих четырех общих классов (в скобках приводится аналогия с физическими и вычислительными системами):
однородные (стабильные) состояния (предельные точки);
периодические структуры (предельные циклы);
хаотическая структура (странные аттракторы);
сложные локализованные структуры (возможная аналогия с универсальными вычислениями).
№ 46
Одномерный клеточный автомат “эволюционирует” дискретно во времени, на каждом шаге переходя к новой строке клеток. Состояние каждой клетки в новой строке определяется применением конкретного правила к значению клетки в предыдущей строке, лежащей непосредственно выше новой клетки. Правило изотропно – это означает, что одно и то же правило определяет значение каждой новой клетки; и правило локально, т.е. в правиле используются значения только соседних клеток. Правило применяется ко всем клеткам в строке одновременно.
№ 47
Генетические законы Конуэя для игры “Жизнь” удивительно просты.
1. Каждая живая клетка, у которой два или три соседа, живет и сохраняется до следующего поколения.
2. Клетка погибает, если у нее более чем три соседа (от недостатка места), совсем нет соседей или только один сосед (от одиночества).
3. Когда рядом с какой-нибудь мертвой (пустой) клеткой есть три живые соседние клетки, то эта клетка становится живой.
4. Клетки погибают и рождаются одновременно. Они образуют одно поколение. За один ход в игре осуществляется переход от одного поколения к другому.
№ 48,49
Игра “Жизнь”.
• Конфигурации, не обладающие в начале игры симметрией, обнаруживают тенденцию к переходу в симметричные формы.
• Существуют конфигурации, которые не имеют предшествующих конфигураций.
• Существуют конфигурации, передвигающиеся по диагоналям.
• С помощью игры “Жизнь” можно моделировать произвольные вычисления.
№ 50,51
• Сущность самоорганизации системы заключается в том, что её структурная реорганизация происходит без явного давления или вмешательства окружающей среды. Другими словами, ограничения на форму (организацию) системы есть внутреннее свойство этой системы, которое является результатом взаимодействия компонентов системы и обычно прямо не связано с физической природой компонентов. Система может эволюционировать во времени или пространстве, находясь в стабильных формах или показывая переходные процессы.
№ 52
• Теория сложных систем изучает системы, для которых использование систем уравнений становится практически невозможным (по причинам их большого числа или просто их отсутствия), а статистические методы еще не действуют.
№ 53,54
• Если рассматриваются дискретные отображения (каскады), то время дискретно: { tn } (n – целое; tk<tl при k < l). Номер n момента tn принимают за независимую переменную. Уравнения движения выражают значения динамических переменных в момент n+1 через их значения в предшествующий момент времени n, например, x(n+1)=F(x(n)).
• Функцию факториал можно рассматривать как динамическую систему с дискретным счетом времени.
№ 55
• Если два отображения сопряжены, то сопряжены (или эквивалентны) и динамические системы, порождаемые этими отображениями. Каждой траектории одной динамической системы соответствует траектория другой динамической. Асимптотические свойства соответствующих друг другу траекторий одинаковы.
№ 56
• Квадратичное полиномиальное отображение имеет три параметра f(x)=ax²+bx+c. Два из этих параметров лишние с точки зрения динамики. Все квадратичные отображения являются топологически сопряженными, причем эта сопряженность достигается с помощью аффинного гомеоморфизма.
№ 57
• Для логистического отображения f:x→ λ x(1-x) при фиксированном 0<λ ≤ ;4 существует самое большее один аттрактор A, и бассейн этого аттрактора - открытое множество, которое плотно в интервале [0, 1]. Аттрактор A является либо циклом, либо бесконечным множеством.
№ 58
• Бесконечная последовательность бифуркаций удвоения для логистического уравнения обладает универсальными свойствами, обнаруженными Фейгенбаумом. Во-первых, значения точек бифуркаций стремятся к пределу λ*=3.569... . Во-вторых, отношение разностей значений управляющего параметра, соответствующих последовательным бифуркациям удвоения периода, с ростом номера бифуркации стремится к пределу:
![]() .
Константа σ = 4,669162… называется постоянной Фейгенбаума.
.
Константа σ = 4,669162… называется постоянной Фейгенбаума.
№ 59
• Пусть динамическая система определяется некоторым параметром. Точками бифуркации называются те значения параметра, при которых система проявляет качественную перестройку своего поведения.
№ 60
• Странные аттракторы возникают в режиме детерминированного хаоса и имеют два существенных отличия: траектория такого аттрактора непериодическая (она не замыкается) и режим функционирования неустойчив (малые отклонения от режима нарастают).
№ 61,62
• Строгая формулировка существенной зависимости от начальных условий такова. Отображение f обладает существенной зависимостью от начальных условий, если существует такое σ>0, что для любого x∈X и U - произвольного открытого множества, содержащего x, существуют такое целое число n > 0 и такая точка y∈U, для которых σ(fn(x),fn(y))>σ.
№ 63
• Число x принадлежит канторову множеству “средних третей” в том и только в том случае, если его можно представить троичной дробью, используя лишь цифры 0 и 2.
• Пусть I - конечный замкнутый или бесконечный интервал в R. Если непрерывное отображение I→I имеет цикл периода 3, то оно имеет и неподвижную точку.
№ 64
• L–системы Фибоначчи и Туэ обладают эффектом эмерджентности: локальные правила переписывания влекут за собой глобальный эффект – простую связь между поколениями.
№ 65
• Можно с помощью L–системы построить кривую на плоскости, топологическая размерность которой равна 2.
№ 66
• Все квадратичные отображения являются топологически сопряженными, причем эта сопряженность достигается с помощью аффинного гомеоморфизма. Причем это остается в силе и для комплексной переменной.
№ 67,68,69
• Одномерный клеточный автомат “эволюционирует” дискретно во времени, на каждом шаге переходя к новой строке клеток. Состояние каждой клетки в новой строке определяется применением конкретного правила к значению клетки в предыдущей строке, лежащей непосредственно выше новой клетки. Правило изотропно – это означает, что одно и то же правило определяет значение каждой новой клетки; и правило локально, т.е. в правиле используются значения только соседних клеток. Правило применяется ко всем клеткам в строке одновременно.
№ 70,71,72
• Доказано существование одномерного клеточного автомата, который является универсальным компьютером.
№ 73
Множество { xi(t0) } считается координатами точки в K-мерном пространстве состояний системы, которое называется пространством состояний. Элемент этого пространства, соответствующий состоянию системы, называется фазовая точка.
№ 74
Для ifs–системы { F1,F2, ... Fm } определяем преобразование Хатчинсона в пространстве компактных евклидовых множеств F(E)=F1(E) ∪ F2(E) ∪ . . . ∪ Fm(E), E ∈ K.
Теорема. Преобразование Хатчинсона является сжимающим отображением на K с расстоянием h. Его коэффициент сжатия равен s = max{ s1, s2, . . . , sm }
Расстояние h определил Хаусдорф.
№ 75
Теорема. Пусть F1,F2,...,Fm - сжимающие отображения на Rn. Для произвольного начального множества E0∈K система итерированных функций En=FE(n- 1), n=1,2,..., где F - преобразование …, сходится в метрике Хаусдорфа к единственному множеству E∈K
Ученый, в честь которого названо преобразование F: Хатчинсон.
№ 76
Существуют два различных алгоритма для построения аттракторов систем итерированных функций. Более эффективно позволяет построить аттрактор системы итерированных функций:
• Рандомизированный алгоритм.
№ 77
Когда множество Жюлиа является несвязным, оно называется пыль Фату и является канторовым множеством на плоскости.
№ 78
Ученый, в честь которого названо множество всех значений параметра c, для которых множества Жюлиа J(fc) связны:
• Мандельброт.
№ 79
Можно легко найти соответствующую систему итерированных функций, для которой аттрактором будет:
• лист папоротника;
• салфетка Серпинского;
• кривая Коха.
№ 80
Можно найти соответствующую L–систему для построения фракталов:
• кривая Пеано;
• кривая Коха;
• салфетка Серпинского.
№ 81
В алфавите L–системе Фибоначчи:
• 2 символа.
№ 82
Длина классического канторова множества:
• 0.
№ 83
Площадь кривой Коха:
• 0.
№ 84
Фрактал – это множество, для которого размерность Хаусдорфа больше топологической размерности.
№ 85
Упорядочим все натуральные числа следующим образом:
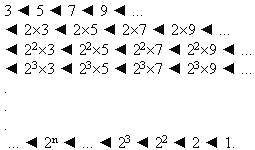
Сначала идут все нечетные числа, потом все нечетные, умноженные на 2, потом - на 4, и т. д. После бесконечного множества таких бесконечных “секций” стоит секция степеней двойки, выстроенных в обратном порядке. Советский математик, определивший данную упорядоченность натуральных чисел:
• Шарковский.
№ 86
Эволюция регулярного (нехаотического) движения, при котором с изменением управляющего параметра происходит бесконечная последовательность удвоения периода, приводящая к возникновению хаотического движения, называется сценарий Фейгенбаума.
№ 87
Для логистического отображения f:x→λx(1-x) мы можем начертить аттрактор для всех λ сразу на одной диаграмме. Такая диаграмма называется бифуркационной диаграммой.
№ 88
Пусть дана дискретная динамическая система (X, f). Точка x0∈X называется периодической точкой периода m, если fm(x0)=xn и fn(x0)≠x0 при 0 < n < m. Каждая из точек xn=fn(x0), n = 1, 2, ..., m-1, также является периодической периода m, и точки x0,x1,...,x|m-1| образуют периодическую траекторию или цикл периода m.
№ 89
Диаграмма (лестница) Ламерея для отображения f:R→R c начальной точкой x0 изображает последовательность образов точки x0 при итерации отображения f.
№ 90
Аттрактор Лоренца является странным аттрактором. Такие аттракторы возникают в режиме детерминированного хаоса и имеют два существенных отличия: траектория такого аттрактора непериодическая (она не замыкается) и режим функционирования неустойчив (малые отклонения от режима нарастают).
№ 91
Финитное экспоненциально неустойчивое движение нелинейной динамической системы называется хаотическим движением.
№ 92
Лоренц обнаружил аттрактор, называемый теперь его именем, который стал первым примером хаотического, или странного аттрактора.
№ 93
Для любой системы с двумя уравнениями финитные движения относятся к одному из следующих типов:
• состоянию равновесия;
• движению, асимптотически стремящемуся к состоянию равновесия;
• периодическому движению;
• движению, асимптотически стремящемуся к периодическому.
№ 94
Как влияет изменение параметров системы на качественные свойства закона движения? Интересно определение граничных значений параметров, при переходе через которые меняется число и/или тип исключительных решений. Такое изменение называется бифуркация.
№ 95,96
Если при любых начальных условиях x0 из некоторой области при достаточно больших временах фазовая точка окажется сколь угодно близко к фазовой траектории A, то такая фазовая траектория называется аттрактором и является исключительной. Множество Ω всех начальных состояний { x0 }, определяющих фазовые траектории, асимптотически притягивающиеся к данному аттрактору A, называется бассейном этого аттрактора.
№ 97
Движение динамической системы в общем случае непериодично. Поэтому исключительными являются фазовые траектории, соответствующие периодическому движению. Для автономных систем – потоков - такие траектории являются замкнутыми кривыми в пространстве состояний. Для дискретных отображений xn+1=F(xn) период движения k должен быть целым. Фазовая траектория, соответствующая закону движения с периодом k, называется циклом длины k.
№ 98
Для автономных систем с фиксированными значениями параметров определение структуры пространства состояний сводится, в первую очередь, к выделению особых (исключительных) фазовых траекторий. Состояние динамической системы в общем случае изменяется со временем. Поэтому исключительными фазовыми траекториями являются неподвижные точки, представляющие состояние равновесия системы.
№ 99
Одна из исторически первых динамических дискретных систем – система с уравнением Fn+1=Fn+Fn-1. Фазовая траектория этой модели с начальными условиями F1=1, F2=1 называется числами Фибоначчи Fn.
№ 100
Ученые обнаружили, что сложные системы сами по себе часто характеризуются следующими важными факторами:
• самоорганизацией;
• нелинейностью;
• динамикой на грани между порядком и хаосом;
• свойством эмерджентности.
№ 101
Простая (детерминированная и контекстно-независимая) L-система содержит компоненты:
• Алфавит - конечное множество V, элементы которого обозначаются обычно буквами a, b, c и т. д. или возможно другими символами.
• Аксиома или инициатор - слово из V, обозначает начальное состояние системы.
• Продукция (или правило переписывания) – отображение символа a∈V в слово w∈V*.
№ 102
• Во время эволюции клеточного автомата изменения состояний клетки происходят параллельно, локально и однородно.
№ 103
• Если использовать метод Ньютона для приближенного численного нахождения корней комплексного многочлена p(z)=zn-1, то комплексная плоскость разделится на n областей. В зависимости от того, в какой области мы возьмем начальную точку, процесс вычисления приведет к одному из n различных корней. Каждая точка границы между областями является одновременно граничной сразу для всех n областей.
| на главную | база по специальностям | база по дисциплинам | статьи |
Другие статьи по теме
