Теоретические основы электротехники.
Установившиеся режимы в линейных электрических цепях.
Кобрина Н.В., Фикс Н.П.
Кафедра ТОЭ
Томск-2001

№ 1
Основные компоненты ЭЦ.
• Источники и приемники.

№ 2
Три множества объектов ЭЦ.
• Ветви, компоненты, узлы.

№ 3
Три типа соединений компонентов ЭЦ.
• Параллельное, последовательное, смешанное.

№ 4
Линейные статические модели компонентов ЭЦ описываются:
• Линейными алгебраическими уравнениями.

№ 5
Тип уравнений, с помощью которых описываются линейные инерционные модели.
• Линейные дифференциальные.

№ 6
Идеализированные элементы ЭЦ делятся на две группы:
• Активные и пассивные.

№ 7
Идеализированную модель емкости описывают электрическими величинами:
• Заряд и напряжение.

№ 8
Идеализированная модель индуктивности описывается:
• Посредством индуктивности и тока.

№ 9
Два типа уравнений математического описания ЭЦ.
• Компонентные и топологические.

№ 10
Уравнения, составленные по законам Кирхгофа относятся:
• К топологическим.

№ 1
Три формы записи комплексного числа.
• Алгебраическая, показательная, тригонометрическая.

№ 2
Формула перехода от алгебраической формы записи комплексного числа A к показательной, если A=A′+jA′′=Ae^jθ.
• A = √((A′)²+(A′′)²); θ = arctg (A′′ / A′).

№ 3
Комплекс сопротивления нагрузки, если напряжение u(t)=120 √2 sin(ωt+120°) B и ток i(t)=4 √2 sin(ωt+165°) A.
• Z=30e^-j45° Ом.

№ 4
Закон изменения тока через конденсатор i_C(t), если u_C(t)=100 √2 sin(100t+45°) B, а C=0,5 мкФ.
• i_C(t)=5 √2 sin(100t-45°) мА.

№ 5
Закон изменения напряжения на катушке индуктивности с параметрами R_κ=100 м, L_κ=0,1 Гн, по которой протекает ток i(t)=5 sin(100t+90°) A.
• u_κ(t)=50 √2 sin(100t+135°) B.

№ 6
Эквивалентная индуктивность двух последовательно соединенных катушек L₁ и L₂, имеющих взаимную индуктивность М, при их согласном и встречном включениях.
• L_согл=L₁+L₂+2 M; L_встр=L₁+L₂-2 M.

№ 7
Вычислить коэффициент связи k_CB двух катушек L₁=0,05 Гн и L₂=0,2 Гн, если M=0,008 Гн.
• 0,8.

№ 8
По катушкам индуктивности L₁ и L₂ протекают токи i₁ и i₂. Выражения напряжений на этих катушках при их встречном включении в комплексной форме.
• U₁=jωL₁I₁-jωMI₂; U₂=jωL₂I₂-jωMI₁.

№ 9
Формула определения полной комплексной мощности двух катушек, обусловленной взаимной индуктивностью при согласном включении.
• S_М=j2ωMI₁I₂cos(θ₁-θ₂).

№ 10
Коэффициент взаимоиндукции двух катушек, если ток в одной из них увеличить в n раз -
• Не изменится.

№ 1
Амплитудно-частотной характеристикой (АЧХ) называют -
• зависимость модуля величины от частоты.

№ 2
Комплексно-частотная характеристика (КЧХ) может быть представлена в форме записей:
• алгебраическая и показательная.

№ 3
Фазо-частотная характеристика (ФЧХ):
• Зависимость фазы от частоты.

№ 4
Резонанс напряжений возникает:
• В последовательном LC-контуре.

№ 5
В ЭЦ при параллельном соединении элементов L и C возникает:
• резонанс токов.

№ 6
Связь напряжения u_L, u_C и u_ВХ при резонансе напряжений, если добротность контура Q>1:
• u_L=u_C>u_BX.

№ 7
Условие, при котором в последовательном колебательном RLC-контуре возникает резонанс:
• Равенство индуктивного и емкостного сопротивлений.

№ 8
Условие резонанса токов в контуре, состоящем из параллельно соединенных конденсатора C и катушки с параметрами R_κ и L_κ для резонансной частоты omega₀.
• .

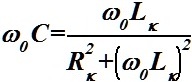№ 9
Резонансная частота ω₀ в параллельном колебательном контуре с параметрами C, R_κ и L_κ:
• .

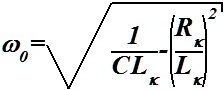№ 10
Перед составлением условия резонанса в сложной цепи со взаимной индуктивностью нужно выполнить:
• Развязку индуктивной связи.

№ 1
В основе метода контурных токов (МКТ) лежат:
• законы Кирхгофа.

№ 2
Уравнения по МКТ для контуров, содержащих источники тока, не составляются.

№ 3
Токи ветвей схемы по МКТ рассчитывают:
• Как алгебраическую сумму соответствующих контурных токов.

№ 4
При расчете токов ветвей схемы по методу узловых потенциалов (МУП) используется:
• закон Ома.

№ 5
Число подсхем при расчете цепи методом наложения (МН) определяется:
• Числом источников питания в схеме.

№ 6
Выражения для расчета тока нагрузки по методу эквивалентного генератора (МЭГ).
• I_H=E_Г / (Z_H + Z_Г); I_H=J_КЗ / (1 + Z_H / Z_Г).

№ 7
ЭДС эквивалентного генератора по МЭГ определяется:
• На основе режимов холостого хода или короткого замыкания.

№ 8
В основе метода наложения лежит:
• принцип наложения суперпозиции.

№ 9
Количество контурных уравнений в МКТ равно:
• Числу независимых контуров схемы.

№ 10
В МКТ влияние токов источников тока учитывают:
• Дополнительным напряжением на сопротивлениях контура за счет токов источников тока.

№ 1,2
Методом эквивалентного генератора определить ток I₃. Параметры схемы: E₁=E₅=15 B; J₄=0,3 A; R₁=10 Ом; R₂=R₅=40 Ом; R₃=12 Oм.

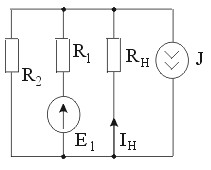
• -0,25 B.
- ток I_H с параметрами: E₁=10 B; J=0,015 A; R₁=R₂=200 Ом.
• E_Г=-3,5 B; R_Г=100 Ом.

№ 3
Методом наложения определить ток I₁ в схеме с параметрами: J=8 A; R₁=R₃=R₄=15 Ом; R₂=30 Ом.

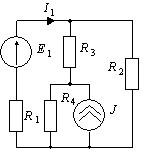
• -1 A.

№ 4
Ток в цепи источника ЭДС I, если параметры схемы:
R=20 Ом; 1/ωC=40 Ом; ωL=80 Ом;
e(t) = 40 √2 sin(ωt+45°) B; J(t) = 1 sin ωt A.

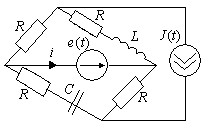
• 2,102+j0,803.

№ 5
Определить ток i₂(t) методом наложения. Параметры схемы:
R₁=X_L1=20 Ом; R₂=100 Ом; X_L2=30 Ом; R₃=X_C=40 Ом;
E₁=56 B=const; e₂(t) = 30 √2 cos ωt B.

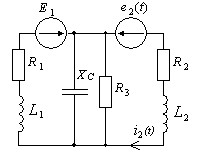
• i₂(t) = 1,6 + 1 cos (ωt-15°) A.

№ 6,7
Токи методом наложения. Сопротивления даны в кОм.

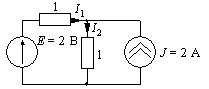
• I₁=0, I₂=2 A.

№ 8
Дано: Е=10 B; J=j10 A; X_C=2 Ом; X_L=R=1 Ом.
Определить ток I₂ методом эквивалентного генератора.

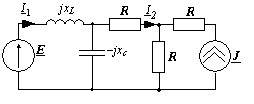
• 2,507-j7,429.

№ 9
Е₁=10 В;
Е₃=j10 B; J=5 A;
X_L=10 Ом; Х_С=50 Ом;
R₁=5 Ом; R=10 Ом.
Ток I_L методом эквивалентного генератора.

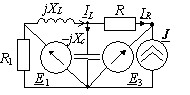
• -j1 A.

№ 10
Определить ток I_C, если:
R=20 Ом; C=500 мкФ;
e₁(t)=20 √2 sin(100t+45°) B; J₂(t)=1 sin(100t+90°) A.

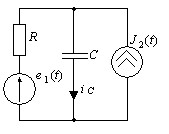
• -0,508+j1,517.

№ 1
Число независимых параметров (коэффициентов) в уравнениях обратимого пассивного четырехполюсника.
• Три.

№ 2
- обратимого симметричного четырехполюсника.
• Два.

№ 3
Сколько опытов необходимо провести для экспериментального определения параметров пассивного четырехполюсника?
• Три.

№ 4
Активные четырехполюсники, содержащие управляемые источники:
• неавтономные.

№ 5
Матрица каких параметров связывает входные и выходные величины, если уравнения записаны для токов четырехполюсника I₁ и I₂?
• Y.

№ 6
Матрица коэффициентов пассивного четырехполюсника, если его уравнения записаны для U₁ и U₂.
• Z.

№ 7
Размерность A-параметров пассивного четырехполюсника: • A₁₁ и A₂₂ - безразмерные величины; A₁₂ измеряют в омах, A₂₁ - в сименсах.

№ 9
Физический смысл параметров пассивного четырехполюсника
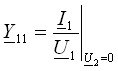и .
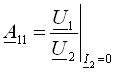• Y₁₁ - комплексная входная проводимость, A₁₁ - комплексный коэффициент передачи по напряжению.

№ 10
Каким числом вторичных (характеристических) параметров характеризуется пассивный четырехполюсник?
• Три.

№ 11
Характеристические сопротивления Z_C1 и Z_C2 несимметричного четырехполюсника.
• .

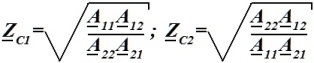№ 12
Коэффициент затухания и фазовый коэффициент пассивного четырехполюсника.
• α = ln U₁/U₂ = ln I₁/I₂; β = ψ_U1 - ψ_U2 = ψ_I1 - ψ_I2.

№ 13
Характеристическое сопротивление симметричного четырехполюсника:
• Z_C1=Z_C2=Z_C; Z_C=√(A₁₂/A₂₁); Z_C=Z_K=Z_X.

№ 13
Две основные полосы частот электрического фильтра.
• Полоса пропускания, полоса затухания.

№ 13
Фильтр низких частот (ФНЧ) и фильтр высоких частот (ФВЧ).
• Полоса пропускания ФНЧ - от ω₁=0 до ω₂, ФВЧ - от ω₁ до ∞.

№ 1
Метод расчета мгновенных значений токов в электрических цепях с несинусоидальными ЭДС.
• Наложения.

№ 2
Комплекс полного сопротивления цепи для k-й гармоники Z_k при последовательном соединении элементов R, L, C?
• Z_k=R+jωkL-j(1/ωkC)=Z_ke^jθk.

№ 3
Мгновенное значение функции тока i(t)=I₀+I_1msin(ωt+ψ₁)+I_2msin(2ωt+ψ₂). Формула для определения действующего значения этого тока.
• .

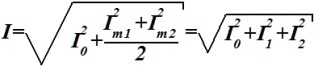№ 4
Выражения мгновенных величин:
i(t)=I₀+I_1msin(ωt+ψ_i1)+I_3msin(3ωt+ψ_i3);
u(t)=U₀+U_1msin(ωt+ψ_u1)+U_3msin(3ωt+ψ_u3).
Формула для расчета активной мощности в цепи.
• P=U₀I₀+U₁I₁cos(ψ_u1-ψ_i1)+U₃I₃cos(ψ_u3-ψ_i3).

№ 5
Как влияет на форму кривой несинусоидального тока по сравнению с кривой напряжения включение индуктивности или включение емкости?
• Индуктивность сглаживает кривую тока, а емкость искажает кривую тока по сравнению с кривой напряжения.

№ 6,7
Ряд Фурье несинусоидальной функции записывается выражением:
a(t)=A₀+A_1msin(ωt+ψ₁)+A_2msin(2ωt+ψ₂).
Вторая форма ряда Фурье через синусные и косинусные составляющие.
• a(t)=A₀+B_1msinωt+B_2msin2ωt+C_1mcosωt+C_2mcos2ωt.
Соотношения между A_1m, A_2m и C_1m, C_2m, B_1m, B_2m.
• B_1m=A_1mcosθ₁; B_2m=A_2mcosθ₂; C_1m=A_1msinθ₁; C_2m=A_1mcosθ₂.

№ 8
Формула расчета полной мощности, если i(t)=I₀+I_1msinωt+I_2msin2ωt; u(t)=U₀+U_1msinωt+U_2msin2ωt.
• .

№ 9
Справедлив ли принцип наложения для комплексных величин токов и напряжений (при разных частотах)?
• Нет.

№ 10
Нельзя построить векторную диаграмму для токов разных гармоник.

№ 1
ЭДС фазы A трехфазного источника e_A=E_msinωt. Начальные фазы ЭДС e_B и e_C при прямом порядке следования фаз:
• ψ_B=-2π/3; ψ_C=2π/3.

№ 2
Провод, соединяющий нулевые точки генератора и нагрузки.
• Нулевой.

№ 3
Напряжения между двумя линейными проводами. Между линейным и нулевым проводами.
• Линейное напряжение. Фазовое напряжение.

№ 4
Соотношение между линейными и фазными величинами при соединении звезда-звезда и симметричной нагрузке.
• U_Л=√3 U_Ф; I_Л=I_Ф.

№ 5
Соотношение между линейными и фазными токами и напряжениями при соединении треугольник-треугольник и симметричной нагрузке.
• I_Л=√3 I_Ф; U_Л=U_Ф.

№ 6
Для симметричного генератора с прямым порядком чередования фаз и соединением обмоток в звезду линейное напряжение U_AB=U_Л. Запишите систему линейных и фазных напряжений этого генератора, используя оператор фазы.
• U_AB=U_Л; U_BC=a²U_Л; U_CA=aU_Л; U_A=U_Лe^-j30°/√3; U_B=a²U_A; U_C=aU_A.

№ 7
В симметричной трехфазной цепи линейный ток I_A=I_Л. Система всех линейных и фазных токов при соединении нагрузки треугольником, используя оператор фазы.
• I_A=I_Л; I_B=a²I_Л; I_C=aI_Л; I_ab=I_Лe^-j30°/√3; I_bc=a²I_ab; I_ca=aI_ab.

№ 8
Наиболее рациональный метод расчета несимметричной трехфазной цепи с соединением звезда-звезда.
• Метод узловых потенциалов.

№ 9
В симметричной трехфазной цепи по методу одного ваттметра можно измерить:
• активную и реактивную мощность.

№ 10
Рассчитать показание ваттметра, включенного на ток I_A и напряжение U_AB.
• P_W=Re(U_ABI_A).

№ 1
Функциями каких двух переменных являются ток и напряжение длинной линии?
• Координаты и времени.

№ 2
Уравнение длинной линии в дифференциальной форме для мгновенных значений тока и напряжения при отсчете расстояния x от начала линии.
• -∂u/∂x=R₀i+L₀∂i/∂t; -∂i/∂x=G₀u+C₀∂u/∂t.

№ 3
Уравнение длинной линии в дифференциальной форме, если входное напряжение - гармоническая функция.
• -dU/dx=Z₀I; -dI/dx=Y₀U.

№ 4
Вторичные параметры ЭЦ с распределенными параметрами и формулы их определения.
• γ=α+jβ=√(Z₀Y₀); Z_B=Z_C=√(Z₀/Y₀).

№ 5
Фазовая скорость распространения бегущей волны.
• c=ν_Ф=dx/dt=ω/β.

№ 6
Какие волны присутствуют в длинной линии, работающей в режиме бегущих волн?
• Падающие волны тока и напряжения.

№ 7
В длинной линии отсутствуют отраженные волны при
• согласованной нагрузке.

№ 8
Уравнение линии с потерями в режиме согласованной нагрузки.
• .

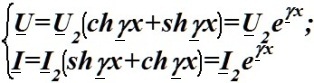№ 9
Условие для первичных параметров в длинной линии без искажений.
• R₀/L₀=G₀/C₀=k.

№ 10
Длинная линия без потерь при отсчете расстояния от нагрузки описывается формулами:
• .

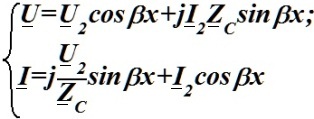№ 11
В линии без потерь параметры α, β, Z_C рассчитываются:
• α=k√(L₀C₀)=√(R₀G₀); β=ω√(L₀C₀); Z_C=√(L₀/C₀).

№ 12
Происходит ли передача электромагнитной энергии от генератора к нагрузке при возникновении стоячих волн?
• Нет.

№ 13
Уравнение длинной линии с потерями в установившемся гармоническом режиме с использованием гиперболических функций (при отсчете расстояния от нагрузки).
• .

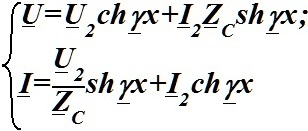№ 14
Формула расчета коэффициента отражения в длинной линии.
• K_u=(Z_H-Z_C)/(Z_H+Z_C).

№ 15
КПД длинной линии при согласованной нагрузке:
• η=P₁/P₂=e^2αl.

№ 16
При передаче электромагнитной энергии от генератора к нагрузке в режиме бегущих волн вся энергия падающей волны потребляется нагрузкой.