Теоретические основы электротехники.
Часть 2.
Переходные и статические режимы в линейных и нелинейных цепях. Электромагнитное поле.
Кобрина Н.В., Фикс Н.П.
Кафедра ТОЭ
Томск-2000

№ 1
Продолжительность переходного процесса теоретически и практически.
• Бесконечность и 5τ.

№ 2
Свободная составляющая является:
• Общим решением однородного дифференциального уравнения.

№ 3
Принужденная составляющая из неоднородного дифференциального уравнения.
• При t → ∞.

№ 4
Если корни характеристического уравнения p₁ и p₂ - вещественные, отрицательные, разные, то
• i_LCB=A₁e^p₁t+A₂e^p₂t.

№ 5
Если корни характеристического уравнения p_1,2=-δ ± jω_CB, то
• u_CCB=Ae^-δtsin(ω_CBt+γ).

№ 6
Если корни характеристического уравнения p₁=p₂=p:
• i_LCB=(A₁+A₂t)e^pt.

№ 7
В цепи второго порядка с L и C определить время апериодического переходного процесса t_ПП.
• t_ПП=5τ₁; τ₁>τ₂.

№ 8
Независимые начальные условия определяются из расчета режима:
• Установившегося при t=-0.

№ 9
Зависимые начальные условия определяются:
• По законам Кирхгофа.

№ 10
Система уравнений в цепи второго порядка для определения постоянных интегрирования при t = 0, если общее решение записано для i_L, а процесс апериодический.
• .

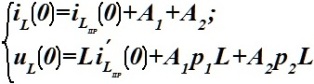№ 11
Система уравнений для определения постоянных интегрирования при t=0 для цепи с L и C, если корни p_1,2=-δ ± jω_CB, а общее решение записано для u_C(t).
• .

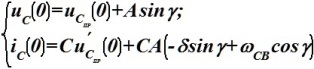№ 12
Первый закон коммутации записывается для величин:
• i_L и ψ_L.

№ 13
Второй закон коммутации:
• u_C и q_C.

№ 14
Операторная схема замещения составляется:
• Для послекоммутационного состояния цепи.

№ 15
Прямая задача операторного метода заключается:
• В переводе функций времени f(t) в операторные изображения F(p) с помощью интеграла Лапласа F(p)=∫^∞₀f(t)e^-ptdt.

№ 16
Обратная задача операторного метода:
• В переводе операторных функций F(p) в функции времени f(t).

№ 17
В операторной форме функция u_L(t)=L (di_L/dt).
• U_L(p)=LpI_L(p)-Li_L(0).

№ 18
В операторной форме функция u_C(t)=1/C ∫ i_C(t)dt.
• U_C(p)=I_C(p)/Cp+u_C(0)/p.

№ 19
Операторным методом при решении прямой задачи операторного метода составляется:
• Алгебраическая система уравнений.

№ 20
Операторное изображение постоянного напряжения U = const.
• U/p.

№ 21
Как учесть ненулевые начальные условия в цепи с индуктивностью при составлении операторной схемы замещения?
• Дополнительная ЭДС Li_L(0) включается в ветвь с индуктивностью по направлению тока.

№ 22
Как учесть ненулевые начальные условия (u_C(0) ≠ 0) в цепи с емкостью при составлении операторной схемы замещения?
• Дополнительная ЭДС u_C(0) / p включается в ветвь с емкостью против тока.

№ 23
Законы Кирхгофа в операторной форме:
• ± ∑ I_k(p)=0; ± ∑ U_k(p)= ± ∑ E_k(p).

№ 24
Формула разложения для тока I_L(p)=A(p)/pB(p), если корни характеристического уравнения B(p)=0 вещественные, отрицательные, разные:
• i_L(t)=A(0)/B(0) + ∑ (A(p_k) / p_kB′(p_k)) e^p_kt.

№ 25
Формула разложения для напряжения U_C(p)=A(p)/B(p), если корни характеристического уравнения B(p)=0 комплексно-сопряженные:
• u_C(t)= ∑ (A(p_k) / B′(p_k)) e^p_kt.

№ 26
При расчете операторным методом нулевой корень дает:
• Принужденную составляющую переходного режима.

№ 27
Вещественная и мнимая части корня при колебательном режиме.
• δ (коэффициент затухания) и ω_CB (частота свободных затухающих колебаний).

№ 28
Зависимость времени переходного процесса от коэффициента затухания.
• t_ПП=5/δ.

№ 29
Определить период свободных колебаний, если известна величина ω_св при затухающем колебательном процессе.
• T_CB=2π/ω_CB.

№ 30
Переходная характеристика цепи зависит:
• От времени t и параметров цепи.

№ 31
Формула интеграла Дюамеля при определении тока на первом интервале:
• i(t)=u(0)g(t)+∫^t₀ u′(τ)g(t-τ)dτ.

№ 32
Переходная характеристика для расчета напряжения на конденсаторе.
• h_u(t)=u_C(t) / U, где U=1B=const.

№ 33
Формула интеграла Дюамеля при определении тока i(t) на втором интервале t₁ ≤ t < t₂, если функция входного сигнала задана графиком

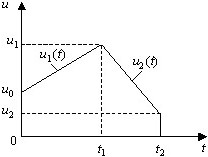
• iII(t)=u0g(t) + ∫t10 (u1′(τ)g(t-τ)dτ) + ∫tt1 (u2′(τ)g(t-τ)dτ).

 

№ 1
Определение фронта прямой и обратной волн.

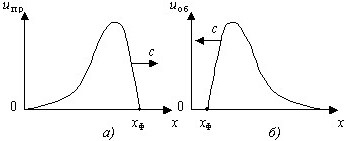
• Фронтом прямой волны называется точка линии с координатой x_ф, для которой u_ПР=0 при x > x_ф и u_ПР ≠ 0 при x < x_ф (рис. а). Координата фронта обратной волны характеризуется условием: u_ОБ=0 при x < x_ф и u_ОБ ≠ 0 при x > x_ф (рис. б).

№ 2
• До тех пор пока волна не достигла конца линии, напряжение и ток вдоль линии в момент времени t распределяются по закону:
u=u_ПР(x,t)=U; i=i_ПР(x,t)=U/Z_C при x < ct;
u=u_ПР(x,t)=0; i=i_ПР(x,t)=0 при x > ct.

№ 3
Графики прямой волны напряжения (тока) соответствуют:

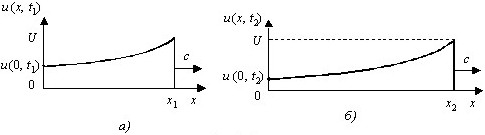
• Экспоненциальной ЭДС источника.

№ 4
Форма отраженной волны повторяет форму падающей волны при любом активном сопротивлении нагрузки (при отражении волны от резистивного элемента).

№ 5
Модуль коэффициента отражения при холостом ходе или коротком замыкании в конце линии:
• 1.

№ 6
Суммарное напряжение u=u_пад+u_отр при холостом ходе в конце линии увеличивается:
• в 2 раза.

№ 7
Суммарный ток i=i_пад-i_отр при холостом ходе в конце линии:
• 0.

№ 8
Суммарный ток i=i_пад-i_отр при коротком замыкании в конце линии увеличивается:
• в 2 раза.

№ 9
Суммарное напряжение u=u_пад+u_отр при коротком замыкании в конце линии:
• 0.

№ 10
Значение тока волны, возникающей при подключении к линии без потерь дополнительного сопротивления R=30 Ом. Параметры линии: U=6,3 кВ; R_H=40 Ом; Z_C=300 Ом.

• 17,5 Ампер.

 

№ 1
Рабочую точку при последовательном соединении линейного и нелинейного сопротивлений наиболее просто можно найти:
• Графическим методом пересечения характеристик.

№ 2
Отрицательным может быть:
• Дифференциальное сопротивление нелинейного элемента.

№ 3
Статическое сопротивление нелинейного элемента:
• R_СТ=U/I.

№ 4
В нелинейной цепи с одним нелинейным элементом определены величины напряжения холостого хода U_xx и тока короткого замыкания I_кз. Определить параметры эквивалентного генератора.
• E_Г=U_xx; R_Г=U_xx/I_кз.

№ 5
Ток нагрузки в методе эквивалентного генератора, если параметры эквивалентного генератора определены (цепь нелинейная), рассчитывается:
• Графическим методом.

№ 6
Коэффициент выпрямления напряжения:
• k_u=U_ср/U.

№ 7
Коэффициент пульсации.
• k_П=U_mП/U_cp.

№ 8
Выражение коэффициента стабилизации стабилизатора напряжения, если U₁ и U₂ - действующие значения напряжений на входе и выходе стабилизатора, а ΔU₁ и ΔU₂ - их относительные приращения.
• .

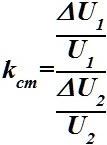№ 9
Какие из методов расчета переходных процессов в нелинейных цепях имеют в качестве основной операции приближенное интегрирование на ЭВМ системы нелинейных дифференциальных уравнений, заданных в форме уравнений состояния - графоаналитические, аналитические или численные?
• Численные.

№ 10
Вольт-амперная характеристика нелинейного элемента при расчете переходного процесса методом последовательных приближений задается:
• В графической форме.

№ 11
Метод последовательных приближений относится:
• К графоаналитическим методам расчета переходных процессов в нелинейных цепях.

№ 12
На принципе припасовывания основан:
• Метод кусочно-линейной аппроксимации.

№ 13
Решения на границах временных интервалов припасовываются:
• Для величин, которые на границах участков не могут изменяться скачком.

№ 14
Уравнения законов Кирхгофа, описывающие нелинейные цепи, относятся:
• К топологическим уравнениям.

№ 15
Эквивалентному нелинейному элементу, которым можно заменить два последовательно соединенных резистивных нелинейных элемента с вольт-амперными характеристиками u₁(i₁) и u₂(i₂), соответствует выражение вольт-амперной характеристики:
• u(i)=(u₁+u₂)(i), где i=i₁=i₂.

№ 16
- два параллельно соединенных резистивных нелинейных элемента:
• u(i)=u(i₁+i₂).

№ 17
Как следует выполнять суммирование вольт-амперных характеристик двух нелинейных элементов, соединенных последовательно?
• Суммировать характеристики параллельно оси тока.

 

№ 1
Материалы, для которых величина магнитной проницаемости не остается постоянной при изменении величины поля и для которых μ_a >> μ₀.
• Ферромагнетики.

№ 2
Зависимость B=f(H) для ферромагнитных материалов.

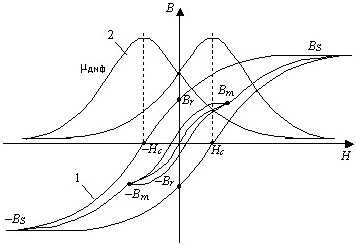
• 1.

№ 3
Зависимость для ферромагнитных материалов нелинейна и неоднозначна.

№ 4
Область, которой определяется удельная (отнесенная к единице объема) энергия, затрачиваемая на перемагничивание от точки B₀ до B_m.

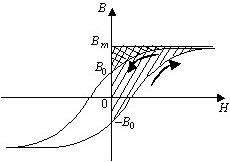
• Площадь под кривой H dB (заштрихованная область).

№ 5
Относительно каких неизвестных решается система уравнений равновесия магнитной цепи:
Ф₁+Ф₂+Ф₃=0
I₁W₁-I₂W₂+H_δ1δ₁-H₂I₂-H_δ2δ₂=0
I₁W₁=H₂I₂+H_δ2δ₂-H₃I₃
• Ф₁, Ф₂, Ф₃.

№ 6
Точка, которая является решением системы уравнений:
Ф₁+Ф₂+Ф₃=0
U_{м ab}=I₁W₁-H₁l₁-H_δ1δ₁
U_{м ab}=I₂W₂-H₂l₂-H_δ2δ₂-H₃l₃
U_{м ab}=-H₃l₃

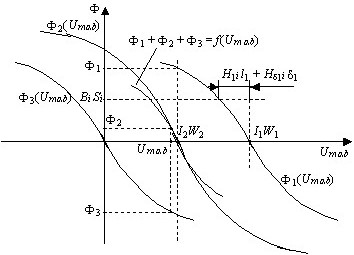
• Точка U_{m ab}.

№ 7
Для уменьшения влияния вихревых токов сердечники электромагнитных материалов делают шихтованными, т.е. набранными из пластин или навитыми из ленты. Чем меньше толщина пластин или ленты, тем меньше, при прочих равных условиях, потери энергии на вихревые токи и тем на больших частотах может работать сердечник.

№ 8
Потери энергии на вихревые токи и гистерезис в сердечнике:
• Потери в стали.

№ 9
Точка на рисунке б, которая при пересечении кривой с осью абсцисс соответствует феррорезонансу напряжений в цепи (рис. а).

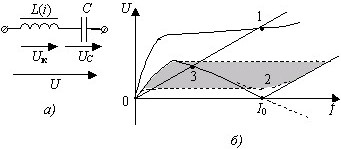
• Точка I₀.

№ 10
Ток рабочей обмотки I_p=I_yW_y / W_p при I_у=const

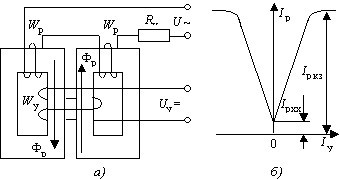
• не зависит от нагрузки.

 

№ 1
• Теорема В.А. Котельникова: любую функцию времени, содержащую гармоники в диапазоне частот 0 - f_max можно передавать с помощью чисел, следующих друг за другом с интервалом в 1 / 2f_max секунд.

№ 2
Для описания дискретных цепей используются:
• Системы разностных уравнений.

№ 3
Сколько динамических уравнений равновесия (уравнений состояния в нормальной форме Коши относительно переменных u_C, i₁, i₂ необходимо составить для расчета цепи?

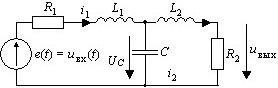
• 3.

№ 4
Система разностных уравнений
i₁[n+1]=0,9i₁[n]-10^-4u_C[n]+10^-4u_вх[n];
i₂[n+1]=0,9i₂[n]+10^-4u_C[n];
u_С[n+1]=u_C[n]+50i₁[n]-50i₂[n];
u_вых[n]=10³i₂[n],
составленная для цепи

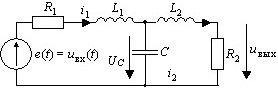
соответствует
• Методу Эйлера.

№ 5
Анализ дискретных сигналов в частотной области осуществляется:
• С помощью дискретизации частотного спектра и дискретного преобразования Фурье.

№ 6
- во временной области:
• С помощью Z-преобразования.

№ 7
Теореме суперпозиции (линейности) (для прямого z-преобразования) соответствует выражение:
• au₁[n]+bu₂[n] ↔ aU₁(z)+bU₂(z), где a и b - постоянные множители.

№ 8
Теорема умножения на n (для прямого z-преобразования):
• u[n]=nu₁[n] ↔ U(z)=-z (dU₁(z) / dz).

№ 9
Теорема умножения на экспоненту (для прямого z-преобразования):
• u[n]=aⁿu₁[n] ↔ U₁(a^-1z).

№ 10
Теорема задержки на N>0 (для прямого z-преобразования):
• u[n]=u₁[n-N]*1[n-N] ↔ U_z(z)=z^-NU₁(z).

 

№ 1
Создается неподвижными заряженными телами и проявляется в виде механической силы, действующей на неподвижный электрический заряд:
• Электростатическое поле.

№ 2
Образуется внутри и вне проводников при прохождении по ним постоянного тока. При этом внутри однородного проводника отсутствует объемная плотность заряда, и линии вектора плотности тока замкнуты. Поле - потенциально.
• Электрическое поле постоянного тока (стационарное электрическое поле).

№ 3
Проявляется силовым воздействием на движущиеся в нем заряженные тела и на неподвижные контуры с постоянным током. Поле имеет вихревой характер.
• Магнитное поле постоянного потока.

№ 4
При электрическом взаимодействии изменяется кинетическая энергия движущейся заряженной частицы вещества .

№ 5
Уравнения Максвелла в интегральной форме записи устанавливают:
• Соотношения между величинами в разных точках поля или на разных отрезках, поверхностях.

№ 6
- в дифференциальной форме записи:
• Соотношения между величинами вблизи одной и той же точки в определенный момент времени.

№ 7
Для потенциальных (безвихревых) полей линейный интеграл по любому замкнутому контуру от напряженности электрического поля, а также от вектора напряженности магнитного поля в области, занятой током, равен:
• 0.

№ 8
Потенциальными полями являются электростатическое поле, электрическое поле постоянного тока (вне источников), магнитное поле постоянного потока вне области с током и квазистатическое поле.

№ 9
Исследование поля в неоднородной среде сводят к расчету его в однородной среде. Влияние на поле неоднородностей учитывают введением в поле вторичных источников - зарядов поляризации, токов намагниченности и т. д., распределенных на границах (в объеме) неоднородностей. Первоначально определяют интегральные уравнения, которые должны соответствовать распределению вторичных источников, а затем по уравнениям поля с учетом заданных вторичных источников решают задачу анализа поля.
• Метод интегральных уравнений.

№ 10
Область поля разбивается на конечное число подобластей - элементов. Внутри каждого элемента искомая функция аппроксимируется, например полиномом, коэффициенты которого выражены через неизвестные значения искомой функции в узлах элемента. Полученные соотношения для коэффициентов подставляют в аппроксимирующий полином, что приводит к уравнению искомой функции в зависимости от узловых значений функции и формы элемента. Это интерполяционное уравнение записывают для каждого элемента согласно сквозной нумерации всех элементов области, после чего с помощью выбранного метода находят уравнения для узловых значений функции.
• Метод конечных элементов.

 

№ 1
Метод переменных состояний допускает применение явных методов интегрирования.

№ 2
Программы автоматизированного анализа цепей, основанные на использовании метода переменных состояния и явных методов интегрирования, относят:
• к 1 поколению.

№ 3
В программах 3 поколения формирование уравнений модели цепи производится с помощью метода узловых потенциалов, причем алгоритмы отличаются простотой и не связаны с решением проблемы топологических вырождений.

№ 4
Программы 3 поколения характеризуются простыми входными языками, широким использованием диалога, наличием графического интерфейса, большим объемом и открытостью для пополнения библиотек моделей компонентов и предоставляют пользователю широкий набор процедур анализа, обработки результатов и оптимизации цепей.

№ 5
Матрица Y_ij для схемы

• .

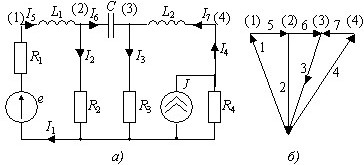
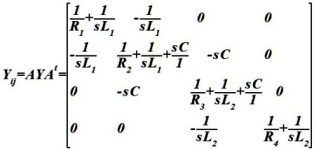№ 6
В уравнениях состояния не содержатся интегралы от неизвестных функций времени.

№ 7
Переменными состояния (в уравнениях состояния) являются:
• Токи индуктивностей и напряжения емкостей.

№ 8
Число независимых уравнений, составленных по методу переменных состояния, равно:
• Числу независимо включенных реактивных элементов.

№ 9
Собственное дерево графа электрической цепи.
• Дерево, которое содержит все источники и все емкостные элементы и не содержит источников тока и индуктивных элементов.

№ 10
Граф цепи

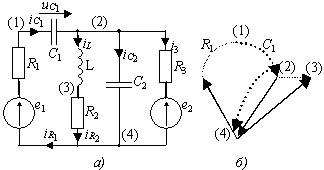
• имеет 3 собственных дерева.