
Теория электрической связи-1
для специальности 021100
Кафедра ТОР
Акулиничев Ю.П.
Томск-2005
№ 1
Сигнал не несет информации, если он:
• детерминированный.
№ 2
Вероятность совместного появления xj и yk в общем случае определяется по формуле:
• p(xj,yk)=p(xj/yk)p(yk).
№ 3
Вероятность появления xj определяется по формуле:
• 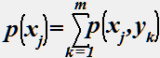 .
.
№ 4
Две дискретные случайные величины X и Y независимы, если при всех j и k:
• p(xj,yk)=p(xj)p(yk).
№ 5
Для полного вероятностного описания m-ичного символа нужно задать:
• ряд распределения.
№ 6
Ожидаемое сообщение считается случайным:
• всегда.
№ 7
При передаче сигнала с понижением скорости ширина его спектра:
• уменьшается.
№ 8
Для полного вероятностного описания последовательности m-ичных символов длиной n нужно задать:
• ряд распределения вероятностей реализаций.
№ 9
Для полного вероятностного описания последовательности n отсчетов непрерывного сигнала нужно задать:
• n-мерную плотность вероятности.
№ 10
Десятичное число 207 в форме 8-разрядного двоичного числа.
• 11001111
№ 11
Двоичное число 1001110 в десятичной форме.
• 78
№ 12
Для полного вероятностного описания отрезка непрерывной случайной функции нужно задать:
• n-мерную плотность вероятности при #math n→∞.
№ 13
Плотность вероятности нормальной случайной величины Х равна:
• ![]() .
.
№ 14
Четверичное число 130 в десятичной форме.
• 28
№ 15
Десятичное число 131 в форме 4-разрядного четверичного числа.
• 2003
№ 16
Ширина спектра (Гц) стандартного аналогового телефонного сигнала.
• 3100
№ 17
Для сигнала в виде последовательности двоичных прямоугольных импульсов без пауз (без возвращения к нулю), передаваемых со скоростью 2000 бит/с, минимальная частота, на которой спектральная плотность мощности обращается в нуль:
• 2000
№ 18
Комбинации 0110110, 1010001, 0111110 сложить по модулю 2. Результат в десятичной форме.
• 89
№ 19
Шестиразрядный АЦП рассчитан на преобразование напряжений в интервале (0, 16) В. На его вход поступает сигнал напряжением 6,342 В. Двоичная комбинацию на выходе АЦП:
• 011001
№ 20
Пятиразрядный АЦП рассчитан на преобразование напряжений в интервале (-3, 13) В. На его вход поступает сигнал напряжением 6,342 В. Двоичная комбинацию на выходе АЦП:
• 10010
№ 21
Четырехразрядный ЦАП рассчитан на преобразование напряжений в интервале (0, 32) В. На его вход поступает двоичная комбинация 1001. Напряжение на выходе (в качестве округленного значения принять напряжение, соответствующее центру нужного интервала:
• 19
№ 22
Пятиразрядный АЦП рассчитан на преобразование напряжений в интервале (-3, 13) В. На его вход поступает двоичная комбинация 10100. Напряжение на выходе:
• 7,25
№ 23
При передаче двоичной последовательности по радиолинии наибольшая полоса потребуется при использовании:
• ЧМ.
№ 24
При передаче двоичной последовательности по радиолинии наименьшая полоса потребуется при использовании:
• КАМ-16.
№ 25
При одинаковой средней мощности полезного сигнала наиболее часто при демодуляции ошибки возникают при использовании:
• КАМ-64.
№ 26
Минимальная частота квантования во времени (отсчетов/с) телефонного сигнала в соответствии с теоремой отсчетов:
• 6800
№ 27
Стандартная частота квантования во времени (отсчетов/с) телефонного сигнала:
• 8000
№ 28
Стандартное количество уровней по напряжению при АЦП телефонного сигнала:
• 256
№ 29
Количество разрядов в стандартном АЦП, применяемом при преобразовании телефонного сигнала:
• 8
№ 30
Декодирование по минимуму расстояния применяется для:
• обнаружения и (или) исправления ошибок в кодовой комбинации.
№ 31
Простейший код с проверкой на четность способен:
• обнаруживать любые ошибки нечетной кратности.
№ 32
Корректирующим называется код, способный:
• обнаруживать и (или) исправлять ошибки, возникающие в канале с помехами.
№ 33
Кодовое расстояние кода численно равно:
• количеству символов, в которых различаются две наиболее близкие друг к другу комбинации в кодовой таблице.
№ 34
Кратность ошибок qo, обнаруживаемых линейным блочным (n,k)-кодом с кодовым расстоянием dкод, подчиняется соотношению:
• q0≤dкод-1.
№ 35
Кратность ошибок qи, исправляемых линейным блочным (n,k)-кодом с кодовым расстоянием dкод, подчиняется соотношению:
• qи≤(dкод-1)/2.
№ 36
Минимальное кодовое расстояние, необходимое для обнаружения всех ошибок кратности до 20 включительно:
• 21
№ 37
Для блочного 10-разрядного двоичного кода, число всех возможных комбинаций:
• 1024
№ 38
Чтобы увеличить корректирующую способность кода, нужно:
• увеличить кодовое расстояние кода.
№ 39
При проведении проверок на четность основной операцией является:
• суммирование символов по модулю 2.
№ 40
Число строк проверочной матрицы (n,k)-кода равно:
• n-k.
№ 41
В системах с переспросом код, применяемый в прямом канале, используется для:
• обнаружения ошибок.
№ 42
Кодовая таблица кода, заданного производящей матрицей
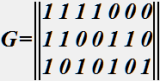 ,
,
содержит:
• 8 комбинаций.
№ 43
Число строк производящей матрицы (n,k)-кода равно:
• k.
№ 44
Число проверок на четность при декодировании комбинации (n,k)-кода равно:
• n-k.
№ 45
О наличии ошибок в принятой комбинации-строке v свидетельствует следующее обстоятельство:
• хотя бы один элемент синдрома не равен нулю.
№ 46
Комбинация кода, заданного производящей матрицей
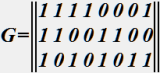 ,
,
содержит:
• 5 проверочных символов.
№ 47
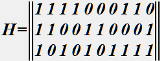 :
:
• 7 информационных символов.
№ 48
Для сверточного кода отношение k/n есть:
• степень кодирования.
№ 49
Для сверточного кода отношение (n-k)/n есть:
• коэффициент избыточности.
№ 50
Для двоичного линейного блочного (n,k)-кода избыточность R определяется по формуле:
• R=(n-k)/n.
№ 51
Если р - это вероятность появления ошибки в одном символе в канале с независимыми ошибками, то вероятность появления q-кратной ошибки в n-разрядной двоичной комбинации определяется по формуле:
• P(q)=Cnqpq(1-p)n-q.
№ 52
Современные корректирующие коды ориентированы на обнаружение (исправление):
• ошибок малой кратности.
№ 53
Минимальное кодовое расстояние, необходимое для исправления всех ошибок кратности до 12 включительно.
• 25
№ 54
Для блочного 9-разрядного двоичного кода с проверкой на четность, число комбинаций в кодовой таблице.
• 256
№ 55
Для двоичного линейного блочного (17,8)-кода, число комбинаций в кодовой таблице.
• 256
№ 56
Количество проверок на четность, проводимых при декодировании комбинации линейного блочного (120,92)-кода.
• 28
№ 57,58
Для заданных производящей G и проверочной H матриц (n,k)-кода при подаче на вход строки a информационных символов комбинация на выходе кодера s определяется по формуле:
• s=aG,
и удовлетворяет условию:
• sHT=0.
№ 59
Для заданных производящей G и проверочной H матриц (n,k)-кода синдром с для принятой комбинации-строки v определяется по формуле:
• c=vHT.
№ 60
Если при декодировании линейного блочного кода синдром оказался равным нулю, то можно гарантировать, что:
• такая комбинация есть в кодовой таблице.
№ 61
Для организации дополнительной проверки на четность в линейном блочном коде следует:
• добавить один проверочный символ.
№ 62
По формуле t=2r-1, где r - количество проверочных символов, определяется:
• количество символов в комбинации кода Хэмминга.
№ 63
Комбинация кода Хэмминга, если в ней 7 проверочных символов, содержит:
• 127 символов.
№ 64
Комбинация циклического кода, способного обнаруживать одиночные и двойные ошибки, если в ней 5 проверочных символов, содержит:
• 31 символов.
№ 65
Кодовое расстояние (255,247)-кода Хэмминга.
• 3
№ 66
Производящая матрица кода равна
 .
.
Закодировать комбинацию 110 и представить в десятичной форме.
• 88
№ 67
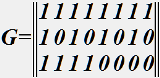 .
.
Закодировать комбинацию 100 и представить в десятичной форме.
• 255
№ 68
Кодовая таблица кода, заданного проверочной матрицей
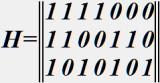 ,
,
содержит:
• 16 комбинаций.
№ 69
Если р - это вероятность появления ошибки в одном символе, то среднее количество ошибок в n-разрядной двоичной комбинации определяется по формуле:
• mq=np.
№ 70
Для двоичного линейного блочного (10,6)-кода, отношение числа разрешенных комбинаций к их общему количеству.
• 16
№ 71
Приведенная таблица

может быть:
• производящей матрицей линейного блочного кода в систематической форме.
№ 72
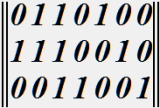 :
:
• проверочной матрицей линейного блочного кода в систематической форме.
№ 73
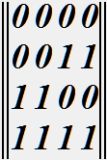 :
:
• кодовой таблицей линейного блочного кода.
№ 74
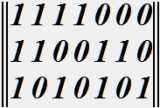 :
:
• проверочной матрицей линейного блочного кода в систематической форме.
№ 75
По формуле t=2r-1, где r - количество проверочных символов, определяется:
• количество символов в комбинации циклического кода.
№ 76
Комбинация кода Рида-Малера первого порядка, если в ней 5 информационных символов, содержит:
• 16 символов.
№ 77
- второго порядка, если в ней один проверочный символ:
• 8 символов.
№ 78
Комбинация циклического кода, способного исправлять одиночные ошибки, если в ней 6 проверочных символов, содержит?
• 63 символов.
№ 79
Кодовое расстояние циклического (63,57)-кода равно:
• (3)
№ 80
- (32,6)-кода Рида-Малера:
• (16)
№ 81
- (16,11)-кода Рида-Малера:
• (4)
№ 82
- (16,5)-кода Рида-Малера:
• (8)
№ 83
Проверочная матрица кода равна H=||1 1 1 1 1 1 1 1||. Закодировать комбинацию 1100010 и представить в десятичной форме.
• 197
№ 84
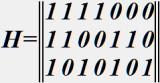 .
.
Номер ошибочного символа в принятой комбинации 1111011.
• 5
№ 85,86
Собственная информация, содержащаяся в значении m-ичного символа, имеющего вероятность pj, равна:
• I=log(1/pj),
и увеличивается при:
• уменьшении вероятности его появления pj.
№ 87
Для оценки величины неопределенности исхода опыта над дискретной случайной величиной используется:
• энтропия.
№ 88
Для m-ичного символа его максимальное значение энтропии Hmax равно:
• Hmax=log m.
№ 89
Для последовательности m-ичных символов длиной n ее максимальное значение энтропии Hn max равно:
• Hn max=n log m.
№ 90,91
Избыточность в сообщении определяется по формулам:
• R=1-H/Hmax.
• R=(L-Lmin)/L.
№ 92
Избыточность в сообщении:
• иногда нужна для повышения помехоустойчивости.
№ 93
Для обеспечения минимальной избыточности в сообщении применяют код:
• Хафмана.
№ 94
Средняя длина кодовой комбинации L для безошибочной передачи сообщения X при помощи m-ичных символов должна удовлетворять соотношению:
• L ≥ H(X) / log m.
№ 95
Причиной появления избыточности в цифровом сигнале является:
• неравновероятность m значений символа и зависимость символов в передаваемой последовательности.
№ 96
При кодировании с минимальной избыточностью для разделения кодовых комбинаций при их последовательной передаче:
• составляют кодовую таблицу так, чтобы никакая комбинация не являлась началом другой, более длинной.
№ 97
Алфавит удается закодировать последовательностью m-ичных символов с нулевой избыточностью, если:
• вероятности всех букв являются отрицательными целочисленными степенями числа m.
№ 98
Пропускная способность С (бит/символ) m-ичного канала без ошибок равна:
• C=log m.
№ 99
Пропускная способность С (бит/символ) двоичного симметричного канала с независимыми ошибками, возникающими с вероятностью р, равна:
• C=1+p log p + (1-p) log (1-p).
№ 100
Пропускная способность С (бит/с) непрерывного канала с ограниченной полосой Δf с белым шумом со спектральной плотностью мощности No в зависимости от средней мощности полезного сигнала Рс определяется по формуле:
• 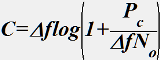 .
.
| на главную | база по специальностям | база по дисциплинам | статьи |
Другие статьи по теме
