Основы теории цепей-2
для специальностей 200700, 200701, 200702, 200703
Теория электрических цепей-2
для специальностей 071700, 075300, 201100, 201400, 201500
Кафедра ТОР
Тельпуховская Л.И., Каминский В.Л.
Томск-2002

Схемные функции (теория).

№ 1
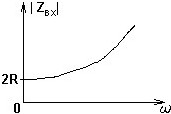
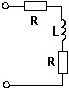
Схема цепи, для которой справедлива представленная зависимость входного сопротивления от частоты.
•

№ 2
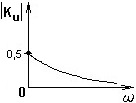
АЧХ коэффициента передачи по напряжению в цепи со следующей схемой.
•

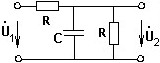№ 3
С какого элемента цепи представленной схемы следует снимать выходное напряжение, чтобы получить АЧХ коэффициента передачи по напряжению следующего вида:

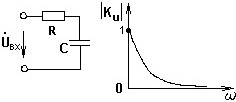
• С емкости.

№ 4
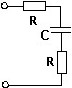
Схема цепи, для которой справедлива представленная частотная зависимость входного сопротивления.
•

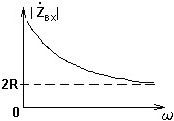№ 5
Значения входного сопротивления цепи на постоянном токе Z(0) и на бесконечно большой частоте Z(∞).

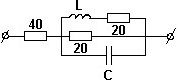
• Z(0) = 50 Ом, Z(∞) = 40 Ом.

№ 6
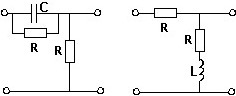
Два варианта схемы цепи, для которых АЧХ коэффициента передачи по напряжению представлена следующей зависимостью:
•

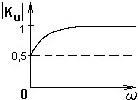№ 7
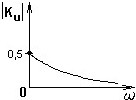
АЧХ коэффициента передачи по напряжению в цепи со следующей схемой:
•

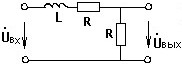№ 8
Каковы значения входного сопротивления представленной цепи на постоянном токе Z(0) и на бесконечно большой частоте Z(∞).

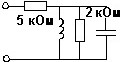
• Z(0) = 5 кОм, Z(∞) = 5 кОм.

№ 9
С какого элемента цепи представленной схемы необходимо снимать выходное напряжение, чтобы получить АЧХ коэффициента передачи по напряжению следующего вида:

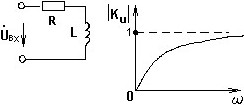
• С индуктивности.

№ 10
Вычислите значения входного сопротивления представленной цепи на постоянном токе Z(0) и на бесконечно большой частоте Z(∞).

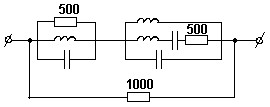
• Z(0) = 0 Ом, Z(∞) = 0 Ом.

Схемные функции (практика).

№ 1
Как изменится амплитуда напряжения на выходе цепи при частоте f=0,6 МГц, если параллельно к резистору R подключить сопротивление, равное 4000 Ом, причем R = 10³ Ом, С=100пФ.

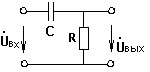
• В 3,36 раз.

№ 2
При каком значении L коэффициент передачи по напряжению будет равен 0,5, если U_вх = 10cos2000t В, R=10 Ом ?

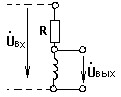
• L ≅ 3 мГн.

№ 3
Выражение АЧХ коэффициента передачи цепи по напряжению и определить граничную частоту полосы пропускания.
• .

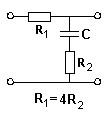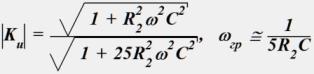№ 4
Коэффициент передачи по напряжению на частоте ω = 1/5 рад/c, если C₁ = 1 Ф, C₂ = 1 Ф, R₁ = R₂ = 5 Ом.

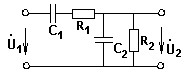
• K_u = 1/3.

№ 5
Для цепи, имеющей представленную ниже схему, определить частоту ω, на которой выходной сигнал в 4 раза меньше входного.
• .

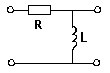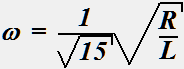№ 6
Выражение для ω_гр цепи, схема которой представлена ниже:
• .

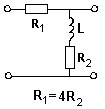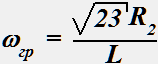№ 7
Определите входное сопротивление цепи, если на некоторой частоте сопротивления участков цепи заданы в омах:
• .

№ 8
Записать выражение для коэффициента передачи по напряжению цепи, схема которой представлена на рисунке ниже, причем: L = 5 Гн, R₁ = 2 Ом, R₂ = 2 Ом, ω = 5 рад/c.

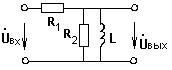
• K_u = j25 / (2+j50).

№ 9
Определить сопротивление цепи, если на некоторой частоте сопротивление каждого элемента указано в омах. Представьте эквивалентную схему замещения на этой частоте.
•

№ 10
На вход последовательной RL цепи подано гармоническое колебание i(t) = cos 10⁶t, мА. Напряжение на индуктивности, если L = 1 мГн.
•

Последовательный колебательный контур. (практика).

№ 1
Укажите, чему равно реактивное сопротивление последовательного контура на граничных частотах полосы пропускания. R - сопротивление потерь.
• |X|=R.

№ 2
Рассчитайте добротность последовательного контура, у которого сопротивление потерь R = 5 Ом, и на некоторой частоте f |X_C|= 225 Ом, |X_L|= 144 Ом.
• 36.

№ 3
Укажите величину напряжения на сопротивлении R при резонансе, если добротность контура Q = 50.

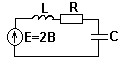
• 2 В.

№ 4
Рассчитайте L и R контура, настроенного последовательно, если амплитуда напряжения на емкости должна быть 10 В, полоса пропускания 15 кГц, емкость контура С = 100 пФ, э.д.с., действующая на контур, имеет амплитуду E_m = 0,1 В.
• 11 мГн, 10 Ом.

№ 5
Рассчитайте полосу пропускания последовательного контура, у которого R = 50 Ом, L = 500 мГн.
• 100 рад/c;
• 16 Гц.

№ 6
Какое шунтирующее сопротивление необходимо подключить к емкости последовательного колебательного контура, чтобы увеличить его полосу пропускания в два раза, если контур имел сопротивление потерь R = 10 Ом, характеристическое сопротивление ρ = 200 Ом.
• 2 кОм.

№ 7
Найдите абсолютную Δf, относительную и обобщенную расстройки контура, при которых ток уменьшится до 0,4 своего резонансного значения, если Q = 100, f_ρ = 5*10⁶ Гц.
• ζ = 3,89, Δf = 97 кГц, Δf / f_ro = 0,0195.

№ 8
Определите амплитуду напряжения на емкости при расстройке Δf = 36 кГц, если к последовательному контуру подключен источник напряжения с амплитудой E = 2 В и частотой 3 Мгц. Контур настроен на частоту источника и имеет следующие параметры: R = 400 Ом, C = 60 пФ.
• 39 В.

№ 9
Определите амплитуду напряжения на емкостном элементе на частоте ω, которая больше резонансной частоты на 0,5%. Добротность контура Q = 40, подводимое к контуру напряжение U = 0,4 cos ω t, В.
• 13 В.

№ 10
Рассчитайте параметры L,C,R,Q последовательного контура, на который действуют одновременно сигнал e_c(t) = 2*cos 2*10⁵t мВ и помеха e_n(t) = 20*cos 10⁶t мВ.
Составляющая напряжения на конденсаторе, созданная сигналом, превосходит составляющую, созданную помехой в 8 раз, и составляющая тока с частотой сигнала равна 0,5 мА.
• L=236 мкГн, С=4210пФ, R= 40 Ом, Q=7,9.

Последовательный колебательный контур. (теория).

№ 1
Определение характеристического сопротивления контура:
• Сопротивление индуктивности или емкости контура на резонансной частоте.

№ 2
Резонансная частота последовательного колебательного контура определяется:
• Величинами емкости и индуктивности контура.

№ 3
Неверное выражение добротности контура:
• Q = 2Δ ω_п / ω_p.

№ 4
В основе определения резонанса напряжений в последовательном колебательном контуре лежит соотношение:
• U_ср = QE_вх.

№ 5
Как изменится резонансная частота последовательного контура при подключении к его конденсатору измерительного прибора, имеющего входную емкость C₀?
• Уменьшится.

№ 6
Относительная полоса пропускания определяется:
• 2Δω / ω_p;
• R / Lω_p.

№ 7
Добротность последовательного колебательного контура при подключении к его конденсатору шунтирующего сопротивления R_ш:
• Уменьшится.

№ 8
Каковы амплитуды напряжения на реактивных элементах последовательного колебательного контура при резонансе, если на входе действует сигнал e(t) = E_mcos ωt:
• U_ср = U_Lp = QE_m.

№ 9
Амплитуда тока на резонансной частоте в последовательном колебательном контуре:
• I_p = E/R.

№ 10
Определение абсолютной настройки контура Δω (или Δf):
• Разность между частотой источника сигнала и резонансной частотой контура.

Параллельный колебательный контур.

№ 1
Входное сопротивление двухполюсника, если сопротивление отдельных участков цепи указаны в омах:

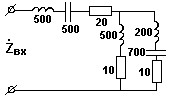
• 12520 Ом.

№ 2
Резонансное сопротивление параллельного контура, у которого L = 100 мкГн, C = 100 пФ, R = 10 Ом.
• 10⁵ Ом.

№ 3
Как следует распределить индуктивность контура между ветвями, чтобы его сопротивление было равно 10 кОм. Контур имеет R=10 Ом, C=600 пФ, L_∑ = 150 мкГн.
• L₁ = 94,5 мкГн, L₂ = 55,5 мкГн.

№ 4
Мощность, выделяемая в простом параллельном контуре, если резонансное сопротивление R_ρ = 40 кОм, амплитуда тока в контуре 0,6 А, добротность Q=30.
• 8 Вт.

№ 5
Мощность на контуре в момент резонанса токов, если резонанс напряжений наступает на частоте 10⁶ рад/с. Параметры контура следующие: R₁ = R₂ = 5 Ом, C = 1000 пФ, L₁ = 500 мкГн, E = 10 В.

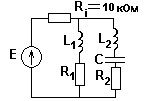
• 2,34 мВт.

№ 6
Схема параллельного контура, для которого резонанс напряжений наступает на частоте ω_p = 1/√(L₂C₁).
•

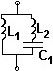
№ 7
Для контура 2-го вида выражение индуктивного коэффициента включения Р, если L₀ = L₁ + L₂.

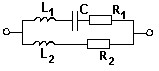
• p = L₂/L₀.

№ 8
Выбрать внутреннее сопротивление генератора R_i, чтобы избирательные свойства контура при подключении генератора к контуру не ухудшились.

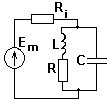
• R_i >> R_p.

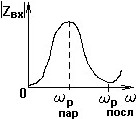
№ 9
Зависимость Z_вх(ω) параллельного контура с разделенными индуктивностями.
•

№ 10
Чему равно сопротивление контура с разделенными конденсаторами на частоте параллельного резонанса, если Q=50, коэффициент включения р=0,5, сопротивление потерь контура R=10 Ом.
• R_рсл = 6,25 кОм.

Связанные контуры.

№ 1
Как изменится входное сопротивление системы связанных колебательных контуров при размыкании ключа, если ω_p1 = ω_p2 = ω_ген, а связь оптимальная?

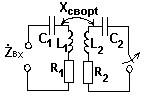
• Уменьшится в два раза.

№ 2
Система из двух колебательных контуров при связи выше критической имеет:
• Три резонансных частоты.

№ 3
Как изменится входное сопротивление системы связанных контуров при замыкании ключа, при условии: ω_p1 = ω_p2 = ω_ген, связь оптимальная?

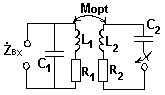
• Уменьшится в два раза.

№ 4
Входное сопротивление системы связанных контуров, если на некоторой частоте сопротивления участков цепей системы указаны в омах.

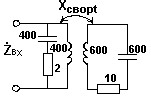
• 80 кОм.

№ 5
Тип резонанса в системе связанных колебательных контуров. Известно, что частота генератора равна 2*10⁶ рад/с, L₁ = 250 мкГн, С₁ = 250 пФ. В системе имеет место оптимальный резонанс.
• Сложный.

№ 6
Эквивалентное (входное) сопротивление связанной системы, последовательно подключенной к генератору, на частоте f=159 кГц. Параметры двух связанных индуктивной связью контуров следующие: L₁ = 510 мкГн, L₂ = 208 мкГн, C₁ = 2000 пФ, C₂ = 5000 пФ, R₁ = 2 Ом, R₂ = 6 Ом, M = 7 мкГн.
• Ż_э = 4,94 + j6,08 Ом.

№ 7
Частоты связи системы их двух одинаковых контуров, настроенных каждый в отдельности на частоту f₀ = 2*10⁶ Гц. Известно, что активное сопротивление каждого контура R=10 Ом, а сопротивление связи X_св = 16 Ом. Емкость каждого контура равна 100 пФ.
• f₂ = 2015,7 кГц, f₃ = 1984,3 кГц;
• f₂ = 16858,7 рад/с, f₃ = 12363,4 рад/с.

№ 8
Рассчитать емкость C₁ первого контура так, чтобы было выполнено условие частного резонанса. Колебательные контуры имеют следующие параметры: L₁ = 200 мкГн, L₂ = 250 мкГн, R₂ = 100 Ом, C₂ = 900 пФ, M = 40 мкГн, f = 700 кГц.
• 270 пФ.

№ 9
Мощность, расходуемая в первом и во втором контурах, если даны два индуктивно-связанных контура со следующими параметрами: L₁ = 400 мкГн, С₁ = 310 пФ, R₁ = 16 Ом,
L₂ = 410 мкГн, С₂ = 290 пФ, R₂ = 14 Ом, f = 460*10³ Гц, U₁ = 100 В, M = 36 мкГн.
• P₁ = 0,205 Вт, P₂ = 5,68 Вт.

№ 10
Мощность, отдаваемая во второй контур, и вид резонанса в системе двух связанных контуров со следующими параметрами: L₁ = L₂ = 0,5 мГн, R₁ = R₂ = 10 Ом, ω_p1 = ω_p2 = 10⁶ рад/c, M = 20 мкГн, e(t) = 4cos10⁶t, В.

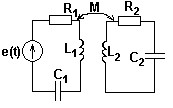
• P₂ = 128 мВт, резонанс индивидуальный.

Четырехполюсники (теория и практика).

№ 1
А-параметры четырехполюсника (ЧП) определяются при режимах работы:
• Х.Х. (холостой ход) на выходе и К.З. (короткое замыкание) на выходе.

№ 2
Система уравнений, для которой матрица параметров [МП] выражается через Y-параметры:
• .

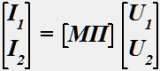№ 3
При каскадном соединении двух четырехполюсников (ЧП) результирующая матрица параметров равна выражению:
• [A] = [A₁]*[A₂].

№ 4
Y-параметры четырехполюсника (ЧП) определяются при:
• Х.Х. на выходе и Х.Х. на входе.

№ 5
Условием максимальной передачи мощности от четырехполюсника в нагрузку является утверждение:
• Равенство комплексно-сопряженных сопротивлений выхода ЧП и нагрузки Ż_выхчп = Ż*_н.

№ 6
Физический смысл и размерность параметра A₁₁.
• Безразмерная величина, обратная коэффициенту передачи ЧП при холостом ходе на выходе.

№ 7
Характеристическими называются параметры ЧП:
• Постоянная распространения, характеристические сопротивления.

№ 8
Результирующая матрица эквивалентных параметров для параллельного соединения двух четырехполюсников:

• [Y] = [Y₁] + [Y₂].

№ 9
Для согласованного ЧП затухание 40 дБ соответствует уменьшению напряжения или тока в:
• 100 раз.

№ 10
Для согласованного ЧП 1 Неп соответствует изменению напряжения или тока в:
• 2,72 раза.

№ 11
Модуль определителя матрицы Y-параметров для четырехполюсника.

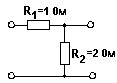
• 0,5.

№ 12
- А-параметров.

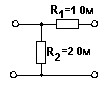
• 1.

№ 13
- Z-параметров.

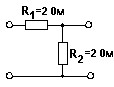
• 4.

№ 14
Коэффициент передачи по напряжению в режиме холостого хода на выходе, при использовании теории четырехполюсников на основе А-параметров, если: Ż₁ = 100 Ом, Ż₂ = jX_C = -j100 Ом, Ż₃ = jX_L = j200 Ом.

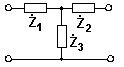
• = 0,9e^{j arctg 0,5}.

№ 15
Характеристические сопротивления Z_C1 и Z_C2 для схемы четырехполюсника, у которого параметры на некоторой частоте указаны в омах.

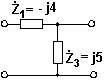
• Ż_C1 = 2 Ом, Z_C2 = 10 Ом.

№ 16
Для Т-образного симметричного четырехполюсника вычислить характеристические сопротивления. Значения элементов указаны в омах.

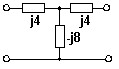
• Z_C1 = 6,95 Ом, Ż_C2 = 6,95 Ом.

№ 17
Характеристическое затухание a_c и фазовая постоянная b_c на основе соотношения g_c = ln(√(A₁₁A₂₂) + √(A₁₂A₂₁)). Параметры указаны на схеме в омах.

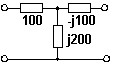
• a_c = 2,12 дБ, b_c = -0,785 рад.

№ 18
Y-параметры ЧП, для которого сопротивления на схеме указаны в омах.

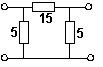
• Y₁₁ = 0,294 См, Y₁₂ = -0,0665 См, Y₂₁ = 0,0665 См, Y₂₂ = -0,294 См.

№ 19
Z-параметры ЧП.

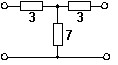
• Z₁₁ = 10 Ом, Z₁₂ = -7 Ом, Z₂₁ = 7 Ом, Z₂₂ = -10 Ом.

№ 20
Характеристическое затухание a_c и характеристическая фазовая постоянная b_c полузвена меньше соответствующих величин a_c, b_c полного звена:
• В два раза.

Фильтры (практика и теория).

№ 1
Если на некоторой частоте ω оба двухполюсника состоят из единственного реактивного элемента, то тип фильтра представленный на схеме:

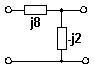
• ФНЧ.

№ 2
Для схемы фильтра, определить частоту среза.

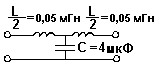
• 2*10⁵ рад/c.

№ 3
Параметры ФНЧ L и С, имеющего ω_ср = 4000 рад/с и характеристическое сопротивление R₀ = 50 Ом.
• С=10 мкФ, L=25 мГн.

№ 4
Параметры L и С ФВЧ, обеспечивающего частоту среза ω_ср = 2000 рад/с и имеющего номинальное характеристическое сопротивление R₀ = 75 Ом.
• С=3,33 мкФ, L=37,5 мГн.

№ 5
Характеристическое сопротивление для Т-образной схемы ФНЧ на частоте ω = 1/2 ω_ср при условии, что номинальное характеристическое сопротивление R₀ = 75 Ом.
• 64,95 Ом.

№ 6
Характеристическое сопротивление для П-образной схемы ФВЧ на частоте ω = 1/2 ω_ср, при номинальном характеристическом сопротивлении R₀ = 75 Ом.
• |Z_СП| = 43 Ом, характер емкостный.

№ 7
Для m=0,6 индуктивность поперечной ветви последовательно-производного фильтра нижних частот типа 'm', при частоте среза ФНЧ типа 'к' равна ω_ср = 4000 рад/с, а номинальное характеристическое сопротивление R₀ = 50 Ом.
• L=13,4 мГн.

№ 8
Для m=0,5 индуктивность поперечной ветви последовательно-производного фильтра верхних частот типа 'm', при частоте среза ω_ср = 2000 рад/с, а номинальное характеристическое сопротивление R₀ = 75 Ом.
• L=18,75 мГн.

№ 9
Для согласованного фильтра затухание в 40 дБ соответствует уменьшению амплитуды напряжения или тока в:
• 100 раз.

№ 10
Затухание ФНЧ на частоте ω = 2ω_ср. Выразить затухание в неперах, децибелах и простых числах.
• 2,64 нп, 23 дБ, 7.

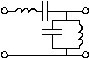
№ 11
Какому типу фильтра соответствует частотная зависимость затухания?
•

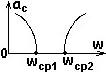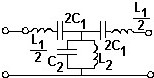
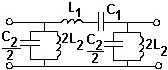
№ 12,13
Схема фильтра, для которого представлена зависимость характеристического сопротивления Z_c от частоты ω.
•
•

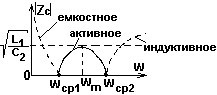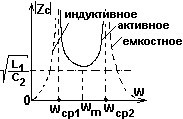№ 14
Тип фильтра:

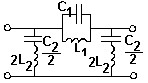
• ПЗФ.

№ 15
Какому типу фильтра соответствует представленная фазовая характеристика?

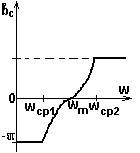
• ППФ.

№ 16
Выражение, соответствующее частоте среза (ω_ср) для схемы:

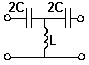
• ω_ср = 1/2√(LC)|.

№ 17
Выражения для характеристической постоянной g_c симметричного звена фильтра.
• ch g_с = A₁₁;
• ch g_с = 1/K_U^xx;
• e^-g_c = K_Uсогл.

№ 18
Последовательно-производное звено ФНЧ типа 'm':
•

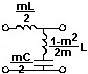
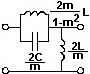
№ 19
Параллельно-производное звено ФВЧ типа 'm':
•

№ 20
Нагрузка фильтра, когда его входное сопротивление равняется характеристическому:
• Z_н = ρ.

Длинные линии (практика).

№ 1
Входное сопротивления короткозамкнутой линии без потерь, если ее длина 48 м, а рабочая длина волны λ = 124 м, волновое сопротивление ρ = 72 Ом.
• -j62,5 Ом, входное сопротивление имеет емкостный характер.

№ 2
Входное сопротивление линии на частоте f = 3*10⁶ Гц, если длина линии равна l=5 м, волновое сопротивление ρ = 100 Ом, и линия нагружена на индуктивное сопротивление, равное 50 Ом.
• 198,2 Ом.

№ 3
Длина воздушной короткозамкнутой линии без потерь, имеющей Ż_вх = j50 Ом, волновое сопротивление ρ = 150 Ом. Частота генератора, питающего линию, 75 МГц.
• 0,2 м.

№ 4
Затухание линии a_c, если волновое сопротивление длинной линии ρ = 100 Ом, а погонное сопротивление линии составляет 230 Ом/км. Примечание: погонной проводимостью пренебречь, a_c ≅ (R/2ρ) + (1/2Gρ).
• 1,15 нп/км.

№ 5
Скорость распространения радиоволн в линии без потерь и длину волны, если линия имеет погонные параметры С=16пФ/м, L=1мкГн/м, частота питающего генератора f=25МГц.
• 2,5*10⁸ м/с, 10 м.

№ 6
Коэффициент бегущей волны в линии, в которой минимальная амплитуда напряжения составляет 2 В, а максимальная - 2,5 В.
• 0,8.

№ 7
Волновое сопротивлене разомкнутой линии, для которой были проведены два измерения: напряжение в конце линии U_к = 400 В, и ток на расстоянии, равном 2 м от конца линии, I=1 А. Длина волны генератора λ = 20 м.
• 235 Ом.

№ 8
Коэффициент отражения в длинной линии, для которой распределение амплитуды напряжения представлено следующим графиком:

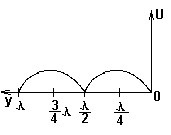
• -1.

№ 9
Коэффициент стоячей волны в длинной линии, если коэффициент бегущей волны равен 0,25.
• 4.

№ 10
Рассчитать нагрузочное сопротивление воздушной длинной линии без потерь так, чтобы входное сопротивление было равно 0. Длина линии l=30 м, ρ = 100 Ом, генератор, питающий линию, работает на частоте f = 2*10⁶ Гц.
• 308 Ом.

Длинные линии (теория).

№ 1
Режим работы длинной линии без потерь, для которой распределение сопротивления по ее длине представлено следующим графиком:

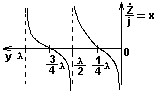
• Режим стоячих волн при холостом ходе на выходе.

№ 2
Коэффициент бегущей волны определяется:
• U_min/U_max.

№ 3
Разомкнутую длинную линию без потерь в точке l = λ/4 можно заменить эквивалентной схемой:
• Настроенным последовательным контуром без потерь.

№ 4
Вид нагрузки длинной линии без потерь, для которой распределение амплитуды тока и напряжения вдоль ее линии представлено на следующем графике:

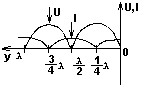
• Ż_н = 0.

№ 5
Эквивалентная схема замещения разомкнутого отрезка линии без потерь длиной l = λ.
•

№ 6
В линии без потерь устанавливается режим бегущей волны при нагрузке:
• Ż_н = ρ.

№ 7
Коэффициент стоячей волны:
• U_max/U_min.

№ 8
Выражение для коэффициента фазы длинной линии.
• β = 2π/λ;
• β = ω√(LC);
• β = ωT/λ.

№ 9
Волновое сопротивление линии без потерь (ρ) определяется выражением:
• ρ = √(L/C);
• ρ = U_пад/I_пад;
• ρ = U_отр/I_отр.

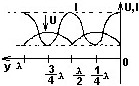
№ 10
Распределение амплитуд напряжения и тока в линии без потерь, нагруженной на активное сопротивление R_н < ρ.
•