Цифровая обработка сигналов
для специальностей 201400, 201500, 200700
Курячий М.И.
Кафедра ТУ
Томск-2004

Цифровые цепи и сигналы.

№ 1
Преобразования (t_преобр) для АЦП:
• Интервал времени от задания аналогового скачка до значения установившегося цифрового кода.

№ 2
Связь числа уровней квантования N и наименьшего числа разрядов m двоичных чисел, кодирующие эти уровни:
• m=Int(log₂N).

№ 3
В АЦП происходит:
• квантование по уровню, дискретизация по времени, кодирование двоичным кодом.

№ 4
Оператор цифровой системы имеет вид: y(nT)=n²x(nT-T).
• Нестационарная система.

№ 5
y(nT)=nTx²(nT-T).
• Нелинейная.

№ 6
y(nT)=nTx(nT+T).
• Физически нереализуемая.

№ 7
y(nT)=(nT)²x(nT+T).
• Физически нереализуемая и нестационарная.

№ 8
y(nT)=(nT)²x(nT+T).
• Физически реализуемая и нестационарная.

№ 9
Физически реализуемая система:
• y(nT)=x(nT-T)+y(nT-2T).

№ 10
Система называется стационарной или инвариантной во времени, если:
• её параметры не изменяются во времени.

Цифровые системы обработки сигналов.

№ 11
Линейная цифровая система:
• Cистема, в которой выполняется принцип суперпозиции.

№ 12
Фильтр при b_j≠0:
• Рекурсивный.

№ 13
Дана структурная схема ЦФ.

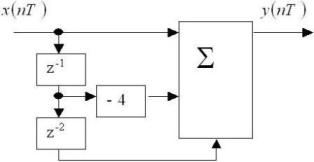
Передаточная функция:
• H(z)=1-4z^-1+z^-3.

№ 14
Всегда рекурсивным является:
• БИХ–фильтр.

№ 15
Основное разностное уравнение для линейных ЦФ:

• Первая сумма описывает нерекурсивную часть фильтра, вторая рекурсивную часть.

№ 16
Разностное уравнение линейного цифрового фильтра

• , описывает рекурсивную часть цифрового фильтра. Если b_j=0, то цифровой фильтр нерекурсивный.

№ 17
Трехкаскадная форма реализации линейного ЦФ, при этом: H₁(z)=1/(1-Z^-1), H₂(z)=1+z^-1, H₃(z)=z^-1.
Формула для передаточной функции всего фильтра:
• H(z) = (z^-1+z^-2) / (1-z^-1).

№ 18
Системная функция вычислителя второй разности:
• H(z) = 1 - 2z^-1+ z^-2.

№ 19
Системная функция сглаживающего звена:
• H(z) = z / (z-K).

№ 20
Системная функция сумматора с ограниченным временем накопления:
• H(z) = (1-z^-M) / (1-z^-1).

Z-преобразование.

№ 21
Функция прямого Z-преобразования:
• .

№ 22
Формула обратного Z-преобразования:

№ 23
f(nT)=Ku(nT). Z-образ.
• (Kz) / (z-1).

№ 24
f(nT)=δ(nT-T)$.
• z^-1.

№ 25
f(nT)=Ku(nT-T).
• K / (z-1).

№ 26
f(nT)=Ku(nT-T)A^n-1.
• K /(z-A).

№ 27
f(nT)=Ku(nT)Aⁿ.
• (Kz) / (z-A).

№ 28
f(nT)=Ku(nT).
• (Kz) / (z-1).

№ 29
f(nT)=r(nT).
• (Tz) / (z-1)².

№ 30
Известен Z-образ функции F(z)=z / (z-1). f(nT):
• u(nT).

Формы реализации цифровых фильтров.

№ 31
Структурная схема цифрового фильтра для канонической формы реализации:

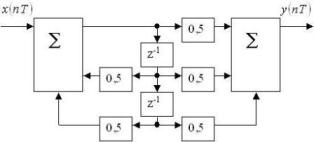
Системная функция:
• H(z) = (0.5+0.5z^-1+0.5z^-2) / (1-0.5z^-1-0.5z^-2).

№ 32
Схема фильтра для прямой формы реализации:

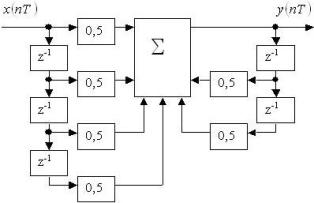
Сколько в структурной схеме данного фильтра для канонической формы реализации будет:
• 3 элемента задержки.

№ 33
Параллельной форме реализации цифрового фильтра соответствует системная функция:
• .

№ 34
Передаточная функция при последовательной форме реализации ЦФ:
• .

№ 35
Задана системная функция: H(z) = (Kz^-1) / (1-z^-1). Структурная схема фильтра:

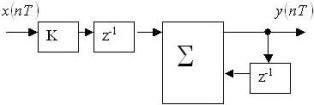
№ 36
Дана передаточная функция ЦФ H(z) = (a₀+a₁z^-1+a₃z^-3) / (1-b₂z^-2-b₅z^-5).
В ЦФ при канонической форме реализации будет входить:
• 5 элементов задержки.

№ 37
Канонической является форма реализации ЦФ:

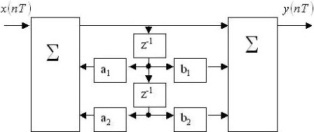
№ 38
Системная функция ЦФ имеет вид (3.2-2.2z^-1) / (0.6z^-1+0.8z^-2-1)
Структурная схема ЦФ в канонической форме:

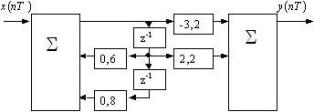
№ 39
Дана структурная схема:

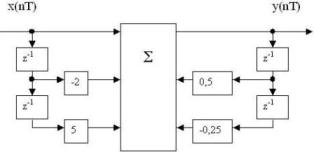
Системная функция:
• H(z) = (1-2z^-1+5z^-2) / (1-0.5z^-1+0.25z^-2).

№ 40
Схема цифрового фильтра:

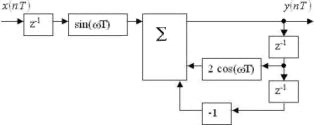
Системная функция:
• H(z) = (sin(ωT)z^-1) / (1-2cos(ωT)z^-1+z^-2).

Характеристики цифровых фильтров.

№ 41
Импульсная характеристика ЦФ:

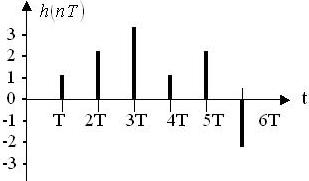
Передаточная функция:
• H(z)=z^-1+2z^-2+3z^-3+z^-4+2z^-5-2z^-6.

№ 42
Дана импульсная характеристика
.
Разностное уравнение:
• y(nT)=x(nT)-x(nT-T).

№ 43
Даны x(nT) и h(nT). y(nT):

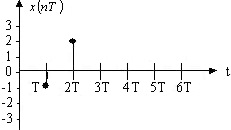
№ 44
Системная функция H(z) = (2-z^-3) / (1-0.8z^-1+0.25z^-2):
• Устойчива.

№ 45
Задан дискретный сигнал
.
Аналитическая форма сигнала:
• x(nT)=δ(nT-T)+2δ(nT-2T)+2δ(nT-3T)+2δ(nT-4T).

№ 46
Коэффициенты для системной функции ЦФ a₀, a₁, a₂, b₁, b₂.
H(z) = (0.7+0.5z^-1-0.4z^-2) / (1+0.4z^-1-0.7z^-2):
• a₀=0.7, a₁=0.5, a₂=-0.4, b₁=-0.4, b₂=0.7.

№ 47
Цифровой фильтр:

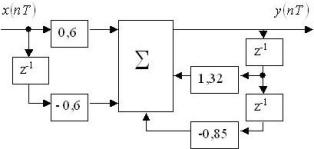
Разностное уравнение:
• y(nT)=0.6x(nT)-0.6x(nT-T)+1.32y(nT-T)-0.85y(nT-2T).

№ 48
Системная функция ЦФ H(z) = (1+z^-1) / (1-b₁z^-1). ЦФ устойчив при:
• |b₁|<1.

№ 49
По схеме цифрового фильтра записать системную функцию H(z):

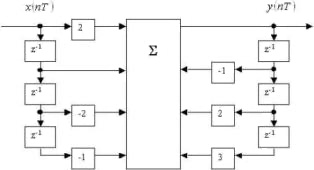
• H(z) = (2+z^-1-2z^-2-z^-3) / (1+z^-1-2z^-2-3z^-3).

№ 50
Разностное уравнение имеет вид y(nT)=0.6x(nT)-0.6x(nT-T)+1.32y(nT-T)-0.85y(nT-2T). Системная функция:
• H(z) = (0.6-0.6z^-1) / (1-1.32z^-1+0.85z^-2).

Нелинейные эффекты в цифровых фильтрах.

№ 51
Формула для вычисления локальной дисперсии шумов на выходе ЦФ:
.

№ 52
Структурная схема цифрового фильтра:

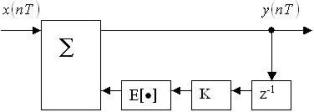
Тип фильтра.
• ЦФ с усечением данных.

№ 53
Разностное уравнение y(nT)=x(nT)+E[Ky(nT-T)], n≥0.
• ЦФ с усечением данных.

№ 54
y(nT)=x(nT)+E[Ky(nT-T)+0.5], n≥0.
• ЦФ с округлением данных.

№ 55
Дисперсия шума АЦП на выходе вычислителя первой разности:
• .

№ 56
- второй разности:
• .

№ 57
- на выходе сумматора на два импульса равна:
• .

№ 58
- три импульса равна:
• .

№ 59
Если C_j – номер младшего разряда в j-й цепи, то дисперсия шума квантования будет равна:
• .

№ 60
Шумы, возникающие в цифровых фильтрах, обусловлены:
• округлением результатов арифметических операций.

Синтез цифровых фильтров с использованием фильтра-прототипа.

№ 61
В методе билинейного преобразования используется замена вида:
• p=2/T*((z-1)/(z+1)).

№ 62
При синтезе ЦФ методом отображения дифференциалов делается замена:
• p=(1-z^-1)/T.

№ 63
Метод синтеза ЦФ, где используется замена операторов p^-N своим выражением для каждого N:
• Z-форм.

№ 64
Нет:
• Синтеза ЦФ по методу отображения интегралов.

№ 65
В методе инвариантного преобразования импульсной характеристики частота дискретизации выбирается исходя из:
• допустимого перекрытия “хвостов” АЧХ.

№ 66
В методе билинейного преобразования трансформация аналоговых частот в цифровые происходит по закону:
• ω_ц=2arctg(ω_aT/2)/T.

№ 67
Способ отображения аналоговых частот в цифровые при билинейном преобразовании:
• ω_a=∞→ω_ц=π/T, ω_a=-∞→ω_ц=-π/T.

№ 68,69,70
В методе билинейного преобразования коррекция частоты производится по закону:
• ω_a=2tg(ω_цT/2)/T.

№ 71
Форма окна Бартлетта в методе временных окон:
• Треугольная.

№ 72,73
Функция, описывающая окно Дирихле (прямоугольное окно):
• .

№ 74
- окно Хемминга:
• .

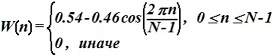№ 75
- окно Бартлетта (треугольное окно):
• .

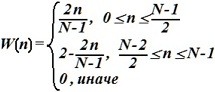№ 76
- окно Ханна:
• .

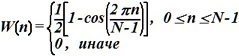№ 77
- окно Блэкмана:
• .

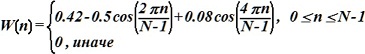№ 78
- окно Кайзера:
• .

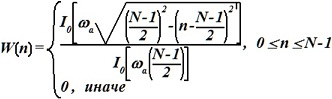№ 79
Временные окна необходимы:
• для уменьшения изрезанности АЧХ в близи крутых склонов.

№ 80
Наименьшая изрезанность АЧХ получается при использовании временного окна:
• Хэмминга.

Построение цифровых фильтров.

№ 81
АЧХ вычислителя первой разности имеет выражение:
• A(ω)=2|sin(ωT/2)|.

№ 82
Вычислители первых и вторых разностей не пропускают постоянную составляющую, потому что они являются:
• цифровыми дифференциаторами.

№ 83
Цифровой интегратор (накапливающий сумматор) условно устойчивый фильтр, потому что:
• сумма отсчетов импульсной характеристики равна бесконечности.

№ 84
Количество отсчетов импульсной характеристики цифрового фильтра с H(z) = (1-z^-M) / (1-z^-1) равно:
• M отсчетов.

№ 85
Цифровой сглаживающий фильтр – это фильтр:
• нижних частот.

№ 86
Цифровой сглаживающий фильтр становится более инерционным, если:
• K→1.

№ 87
Значение АЧХ сглаживающего фильтра с H(z)=z/(z-K) на нулевой частоте равна:
• A(0)=1/(1-K).

№ 88
Универсальная базовая ячейка (УБЯ) в режиме интегрирования имеет коэффициент передачи по постоянной составляющей:
• H_и(1)=1.

№ 89
- в режиме дифференцирования:
• H_и(1)=0.

№ 90
Универсальная базовая ячейка (УБЯ) устойчива, если коэффициент 0.5<A<∞. При этом сглаживающие свойства УБЯ максимальны, если:
• A→∞.

Частотные характеристики цифровых фильтров.

№ 91
Комплексная частотная характеристика получается путем подстановки в системную функцию H(z) выражения для z:
• z=exp(jωT).

№ 92
Величина периода амплитудно-частотной характеристики цифрового фильтра:
• 2π/T.

№ 93
- фазочастотной:
• 2π/T.

№ 94
Групповое время запаздывания ЦФ имеет период повторения по частоте:
• 2π/T.

№ 95
Амплитудно-частотная характеристика ЦФ:
• A(ω)=|H(exp(jωT))|.

№ 96
Фазочастотная характеристика ЦФ:
• θ(ω)=arg(H(exp(jωT))).

№ 97
Групповое время запаздывания цифрового фильтра:
• τ(ω) = -(dθ(ω)) / (dω).

№ 98
Тип цифрового фильтра по виду АЧХ определяется на:
• главном интервале частот от 0 до π/T.

№ 99
Комплексная частотная характеристика цифрового фильтра имеет период повторения:
• 2π/T.

№ 100
• Амплитудно-частотная характеристика цифрового фильтра четна, фазочастотная – нечетна.

Продолжение в “Системы цифровой обработки сигналов” ⇒