
Вычислительная математика
Мицель А.А.
(Кафедра АСУ)
Томск-2000
№ 1
Полная погрешность при использовании численных методов равна:
• сумме погрешностей модели, метода и округления результата.
№ 2
В числе 1,003508
• все цифры значащие.
№ 3
Число 0,001526 имеет абсолютную погрешность 0,7е-6. Определить, верна ли четвертая значащая цифра числа:
• в широком смысле.
№ 4
Округляя число 5,31507 до трех значащих цифр, получим:
• 5,32
№ 5
Приближенным числом называется:
• число, незначительно отличающееся от точного.
№ 6
Даны приближенные числа: а1=13,456; а2=567,234; а3=123,508 и их абсолютные погрешности: Δ1=0,03; Δ2=0,2; Δ3=0,01. Абсолютная погрешность алгебраической суммы этих чисел:
• <= 0,24.
№ 7
Даны приближенные числа: а1=13,456; а2=567,234; а3=123,508 и их абсолютные погрешности: Δ1=0,03; Δ2=0,2; Δ3=0,01. Относительная погрешность произведения этих приближенных чисел:
• >=0,24.
№ 8
Со сколькими знаками нужно взять число √21, чтобы относительная погрешность была не более 1% (в узком смысле). Указать наименьшее число знаков.
Ответ (2)
№ 9
Какова относительная погрешность корня третьей степени из числа а, если относительная погрешность этого числа δ=0,3.
Ответ (0.1)
№ 10
Устойчивым называется такой алгоритм, при реализации которого:
• Накопления погрешности не происходит.
№ 11
При измерении длины пути получен результат L=25.2 км с точностью до 2 м, а при измерении площади получен результат S=1500 м² с точностью до 30 м². Вычислить абсолютную и относительную погрешности (в процентах) обоих результатов. Ответ: Δ1=0.002; δ1=0.008; Δs=30; δs=2.
№ 12
Число Eta называют корнем k-той кратности, если при x=Eta:
• обращаются в нуль функция f(x) и все ее производные до (k-1)-го порядка включительно.
№ 13
На отрезке [a,b] существует хотя бы один корень уравнения f(x)=0, если:
• f(a)*f(b)<0.
№ 14
Методом половинного деления уточнить корень уравнения до трех верных знаков: f(x)=x4+2x3-x-1, лежащий на отрезке [0,5;1].
• (0.867)
№ 15
Найти корень уравнения методом половинного деления с тремя верными знаками: f(x)=2x-cosx; на интервале #math [0,π/2]
• (0.450)
№ 16
Найти методом хорд положительный корень с точностью до 0.002 f(x)=x3-0.2x2-0.2x-1.2 на интервале [1,2].
• (1.198)
№ 17
Дана матрица:
-1 2 3 -2 4 8 -3 7 2Получить нормальную матрицу.
14 31 25 31 69 52 25 52 77
№ 18
Укажите среди предложенных матриц симметричные:
| 1) |
0 0 0 1 0 0 0 1 0 0 1 1 0 1 1 1 | 2) |
0 0 0 0 0 0 1 1 0 1 1 1 1 1 1 1 | 3) |
0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 0 | 4) |
2 3 3 3 3 3 3 3 3 3 2 3 3 3 3 1 |
№ 19
Укажите среди предложенных матриц единичную:
| 1) |
1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 | 2) |
0 0 0 0 0 0 1 1 0 1 1 1 1 1 1 1 | 3) |
0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 0 | 4) |
1 1 1 0 1 1 0 1 1 0 1 1 0 1 1 1 |
№ 20
Найдите определитель матрицы
1 2 3 4 5 6 7 8 9методом Гаусса.
• (0)
№ 21
Найдите определитель матрицы
3 4 5 1 2 3 8 7 1методом Гаусса.
• (-10)
№ 22
Вычислить определитель 3-го порядка, элементы которого заданы условием аij=min(i,j). Применить метод Гаусса.
• (1)
№ 23
Вычислить элемент а11 обратной матрицы A-1. Использовать метод Гаусса.
| A= |
1 2 -1 3 0 2 4 -2 5 |
№ 24
Вычислить элемент а11 обратной матрицы A-1. Использовать метод Гаусса.
| A= |
3 2 1 4 5 2 2 1 4 |
№ 25
Значения неизвестных величин при решении СЛАУ методом Гаусса находят:
• на этапе обратного хода.
№ 26
Сумма квадратов элементов каждой строки ортогональной матрицы равна:
• 1.
№ 27
Определитель ортогональной матрицы равен:
• 1 или -1.
№ 28
Укажите переопределенную систему уравнений:
• x1+x2=0; x1+5=15; x2+10=0
№ 29
Решите систему методом Гаусса. Результат запишите через запятую.
1. 7x1+2x2+3x3=15;
2. 5x1-3x2+2x3=15;
3. 10x1-11x2+5x3=36.
• (2, -1, 1)
№ 30
Идея метода наименьших квадратов состоит в:
• Минимизации суммы квадратов невязок.
№ 31
N-тый член геометрической прогрессии равен:
• an=a1*qn-1.
№ 32
Решить систему методом ортогонализации. Результат записать через запятую.
1. x1+x2+x3-3=0;
2. 2x1+x2+x3-4=0;
3. x1+3x2+x3=0.
• (1, 1.5, 3.5)
№ 33
Основная идея метода Зейделя заключается в том, что при вычислении (k+1)-го приближения неизвестной величины xi
• учитываются значения (k+1)-го приближения величин x1, x2, ..., xi-1.
№ 34
Нормальная система вида Cx=d обладает следующими свойствами:
• матрица С - симметричная, положительно определена и диагональные элементы положительны.
№ 35
Собственные числа матрицы - это:
• корни характеристического уравнения.
№ 36
Поиск решения системы Ax=b эквивалентен:
• поиску минимума функции F(x)=F(x1,x2,...,xn), где F(x)=(1/2) xTAx-xTb.
№ 37
Необходимое и достаточное условие минимума функции F(x):
• grad F(x)=0.
№ 38
Решением системы Ax=b является:
• x=A-1*b.
№ 39
Собственные значения матрицы А некоторой СЛАУ равны: (1,2,3/4,4). Найдите знаменатель q геометрической прогрессии, со скоростью которой будет сходиться метод наискорейшего спуска.
• (3/5)
№ 40
Поставьте в соответствие указанным методам решения СЛАУ формулы их итерационных процессов.
Методы:
1. покоординатного спуска;
2. наискорейшего спуска;
3. сопряженных градиентов.
Формулы:
1. xk+1=xk-ak*F´xk)
2. xk+1=xk-ak*pk
3. 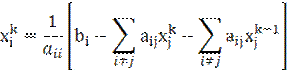
Введите в ответ номера формул для соответствующих методов через пробелы.
• (3 1 2)
№ 41
Вычислить собственные числа матрицы
| A= |
1 -3 3 -2 -6 13 -1 -4 8 | . Использовать метод Данилевского. |
№ 42
Вычислить собственные числа матрицы
| A= |
0 1 0 -4 4 0 -2 1 2 | . Использовать метод Данилевского. |
№ 43
Пусть были найдены значения полинома P(xj) в точках xj∉ [a,b]. При этом функция f(x) задана на интервале [a,b]. Проведенная операция является:
• экстраполяцией.
№ 44
Найдите величину q для интерполяционной формулы Ньютона по следующим данным: x0=1; x1=1,5; x2=2.
• (1)
№ 45
Материальная точка движется прямолинейно. Закон движения S=f(t) представлен в виде таблицы:
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 0 | 2 | 10 | 30 | 68 | 130 | 222 |
| Δ S | 2 | 8 | 20 | 38 | 62 | 92 | |
| Δ2 S | 6 | 12 | 18 | 24 | 30 | ||
| Δ3 S | 6 | 6 | 6 | 6 | |||
| Δ4 S | 0 | 0 | 0 |
• (37.75)
№ 46
Материальная точка движется прямолинейно. Закон движения S=f(t) представлен в виде таблицы:
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 0 | 2 | 10 | 30 | 68 | 130 | 222 |
| Δ S | 2 | 8 | 20 | 38 | 62 | 92 | |
| Δ2 S | 6 | 12 | 18 | 24 | 30 | ||
| Δ3 S | 6 | 6 | 6 | 6 | |||
| Δ4 S | 0 | 0 | 0 |
• (21)
№ 47
Пусть f(x)=√(1-x²), x∈ [-1; 1]. Аппроксимируйте функцию полиномом Чебышева 5-ой степени. Запишите найденные коэффициенты полинома в виде долей числа π через запятую.
• (2/π, -8/3π, -32/15π)
№ 48
Задана функция в виде таблицы:
| x0 | x1 | x2 | x3 | x4 | x5 | |
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 1 | 5 | 21 | 55 | 113 | 201 |
| Δ y | 4 | 16 | 34 | 58 | 88 | |
| Δ2 y | 12 | 18 | 24 | 30 | ||
| Δ3 y | 6 | 6 | 6 |
• (9,.12)
№ 49
| x0 | x1 | x2 | x3 | x4 | x5 | |
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 1 | 5 | 21 | 55 | 113 | 201 |
| Δ y | 4 | 16 | 34 | 58 | 88 | |
| Δ2 y | 12 | 18 | 24 | 30 | ||
| Δ3 y | 6 | 6 | 6 |
• (3,.75,9)
№ 50
Подобрать аппроксимирующий полином 2-ой степени y=a0+a1x+a2x² для данных
| x | 0.78 | 1.56 | 2.34 | 3.12 | 3.81 |
| y | 2.50 | 1.20 | 1.12 | 2.25 | 4.28 |
• (5, -4, 1)
№ 51
Как изменятся коэффициенты aj полинома Чебышева Pj(t) при умножении полинома на число α?
• уменьшатся в α раз.
№ 52
Найти значения линейного полинома вида S(x)=3x-6 в точках x0=0, x1=2. В ответе записать значения через запятую.
• (-6, 0)
№ 53
Найти значения линейного полинома вида S(x)=2x+11, в точках x0=0, x1=1. В ответе записать значения через запятую.
• (11, 13)
№ 54
Коэффициенты b0, b1 параболического сплайна равны соответственно 5 и 17. Шаг сетки равен 2. Найти коэффициент C0.
• (3)
№ 55
Присоединение новых слагаемых к ортогональной системе функций с коэффициентами Фурье:
• увеличивает точность аппроксимации.
№ 56
Полиномы Лежандра образуют ортогональную систему на отрезке:
• [-1,1]
№ 57
Коэффициенты разложения функции F(x)=sin(x) в ряд по полиному Лежандра с нечетными номерами.
• не равны 0.
№ 58
Коэффициенты с нечетными номерами разложения функции F(x)=|x| в ряд по полиному Лежандра.
• равны 0.
№ 59
Полиномы Чебышева образуют на отрезке [-1,1] ортогональную систему полиномов с весом:
• (1-x²)-1/2
№ 60
Что принято называть некорректностью задачи дифференцирования:
• увеличение погрешности дифференцирования при уменьшении шага сетки.
№ 61
Регуляризацией дифференцирования по шагу называется:
• процедура выбора шага сетки в зависимости от погрешности измерения значений функции.
№ 62
Даны значения аргумента X={0,1,2,3,4}. Значения функции в этих точках Y(x)={1,2,3,4,5}. Найти коэффициенты аi линейного сплайна.
• (1, 2, 3, 4, 5)
№ 63
Функция задана таблично:
| x | 2 | 4 | 6 |
| F(x) | 4 | 16 | 36 |
• (16, 36)
№ 64
Найти коэффициенты аi кубического сплайна, если известно, что в точках X={x1,x2,x3,x4,x5}={0,1,2,3,4} функция Y(x)={1,2,9,16,23}. Значение выражения: а1*а2.
• (2)
№ 65
Дана функция F(x), x∈ [a,b]. Как заменить аргумент функции x на новый (y), чтобы y∈ [-π, π]:
• y=-π+2π(x-a)/(b-a).
№ 66
Дана функция F(x), x∈ [0,1]. Замените аргумент функции x на новый (y), чтобы y∈ [-π, π]:
• y=-π+2πx.
№ 67
Дана функция F(x), x∈ [0,1]. Замените аргумент функции x на новый (y), чтобы y∈ [-1, 1]:
• y=2x-1.
№ 68
Функцию f(x)=|x| на отрезке [-1;1] аппроксимировать полиномом Лежандра 3-ой степени. В ответ записать коэффициенты полинома С0, С1, С2 через запятую, в виде десятичных дробей.
• (1/2, 0, 5/8)
№ 69
Найти значение полинома Лежандра 3-го порядка в точке x=1.
• 1
№ 70
Численное вычисление интеграла функции одной переменной называется:
• квадратурой.
№ 71
Кубатурой называется:
• вычисление интеграла функции двух переменных.
№ 72
Шаг равномерной сетки вычисляется по формуле (b,a-границы, n-число узлов):
• h=(b-a)/(n-1).
№ 73
Найти коэффициенты Котеса Нi, если #math b=1, a=0, А0=2/3, А1=-1/3, А2=2/3. В ответ записать сумму коэффициентов Нi.
• (1)
№ 74
Найти коэффициент Котеса Н2, если Н0=1/3, Н1=1/3. Ответ записать в виде обыкновенной дроби.
• (1/3)
№ 75
Найти интеграл по формуле трапеций для функции, заданной таблично:
| x | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| y | 1 | 2 | 3 | 4 | 5 | 6 |
№ 76
Найти интеграл по формуле прямоугольников для функции, заданной таблично:
| n | 0 | 1 | 2 | 3 | 4 | 5 |
| x | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| y | 1 | 2 | 3 | 4 | 5 | 6 |
№ 77
Найти интеграл по формуле Симпсона для функции, заданной таблично:
| n | 0 | 1 | 2 | 3 | 4 |
| x | 0 | 0.1 | 0.2 | 0.3 | 0.4 |
| y | 1 | 1.2 | 1.3 | 1.4 | 1.5 |
№ 78
Найти интеграл по формуле трапеций для функции, заданной таблично:
| x | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
| y | 1 | 2 | 3 | 4 | 5 | 6 |
№ 79
Найти интеграл по формуле прямоугольников для функции, заданной таблично:
| n | 0 | 1 | 2 | 3 | 4 | 5 |
| x | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
| y | 1 | 2 | 3 | 4 | 5 | 6 |
№ 80
Найти интеграл по формуле Симпсона для функции, заданной таблично:
| n | 0 | 1 | 2 | 3 | 4 |
| x | 0 | 0.2 | 0.4 | 0.6 | 0.8 |
| y | 1 | 1.2 | 1.3 | 1.4 | 1.5 |
№ 81
Одним из признаков несобственного интеграла является:
• бесконечный интервал интегрирования.
№ 82
Функция 1/(x-1) имеет в точке x=1:
• разрыв 2-го рода.
№ 83
Функция (1/x) имеет в точке x=0 :
• разрыв 2-го рода.
№ 84
Найти правосторонний и левосторонний пределы функции f(x)=1/(1+21/x) в точке x=0. В ответе укажите сумму пределов.
• (1)
№ 85
Уравнение y´=y²+x+1 является:
• обыкновенным дифференциальным уравнением 1-го порядка.
№ 86
Укажите критерий останова метода последовательных приближений решения обыкновенных дифференциальных уравнений:
• max| y(n)(x)-y(n-1)(x) |<ε.
№ 87
Приближенные методы решения обыкновенных ДУ позволяют:
• получить решение как предел y(x) некоторой последовательности yn(x), причём yn(x) выражается через элементарные функции или при помощи квадратур.
№ 88
Численные методы решения обыкновенных ДУ позволяют:
• вычислить приближённые значения искомого решения y(x) на некоторой сетке значений аргумента x.
№ 89
Метод Пикара решения обыкновенных ДУ вида y´=f(x,y) основан:
• на замене уравнения эквивалентным интегральном уравнением.
№ 90
Решить методом Рунге-Кутта 1-го порядка уравнение: y´=y+x; x∈ [0,1]; y(0)=0=y0; h=0.5.
В ответ запишите сумму y0+y1+y2.
• (0.25)
№ 91
Решить методом Рунге-Кутта 1-го порядка уравнение: y´=y+x+1; x∈ [0,1]; y(0)=0=y0; h=0.5. В ответ запишите сумму y0+y1+y2.
• (2)
№ 92
Решить методом Рунге-Кутта 2-го порядка уравнение: y´=y+x; x∈ [0,1]; y(0)=0=y0; h=0.5. В ответ запишите y2.
• (1)
№ 93
Решить методом Рунге-Кутта 2-го порядка уравнение: y´=y+x+1; x∈ [0,1]; y(0)=0=y0; h=0.5. В ответ запишите целую часть суммы y1+y2.
• (2)
№ 94
Пусть x [c,d], s∈ [a,b]. Ядро уравнения Фредгольма K(x,s) задается:
• на прямоугольнике [a≤s≤b, c≤x≤d].
№ 95
При каких значениях |λ| сходится решение интегрального уравнения Фредгольма 2-го рода с ядром K(x,s)=1/(5+x+s), x∈ [0,1]:
• |λ|<5.
№ 96
- с ядром K(x,s)=cos(x+s); x∈ [0,π]:
• |λ|<1/π.
№ 97
- с ядром K(x,s)=exp(-x-s), x∈ [0,1]:
• |λ|<1.
№ 98
Под неустойчивостью интегрального уравнения 1-го рода понимают:
• небольшие изменения в правой части ведут к существенным изменениям решения.
№ 99
При каких значениях |λ| сходится решение интегрального уравнения Фредгольма 2-го рода с ядром K(x,s)=1/(3+x+s), x∈ [0,1]:
• |λ|<3.
№ 100
- с ядром K(x,s)==sin(x+s), x∈ [-|π/2|,π/2]:
• |λ|<1/π.
| на главную | база по специальностям | база по дисциплинам | статьи |
Другие статьи по теме
