Вычислительные методы
для специальностей 220300
Бабак Л.И.
Кафедра КСУП
Томск-2002

№ 1
Численные методы – это методы, основанные:
• на сведении решения задач к элементарным арифметическим действиям над числами.

№ 2
Порядок проведения вычислительного эксперимента:
1) Формулировка задачи исследования, выбор физической модели объекта.
2) Построение математической модели объекта.
3) Выбор (построение) численного метода решения задачи.
4) Реализация метода (алгоритма) в виде программы для ЭВМ.
5) Проведение вычислений и анализ результатов.
6) Корректировка модели, численного метода (алгоритма) или программы.

№ 3
Неустранимая погрешность вычислительного эксперимента – это погрешность, связанная:
• с погрешностями математической модели.

№ 4
Вычислительная погрешность численного эксперимента – это погрешность, возникающая из-за:
• ошибок округления чисел в ЭВМ.

№ 5
Соотношение между погрешностями математической модели Δ_mm, численного метода Δ_чм и округления Δ_окр:
• Δ_окр<Δ_чм<Δ_мм.

№ 6
В результате решения некоторой вычислительной задачи по значению исходной величины x определяется значение искомой величины y. Задача называется устойчивой по параметру y, если:
• малое приращение x приводит к малому приращению y.

№ 7
Является численно устойчивой:
• задача численного интегрирования (вычисления определенного интеграла).

№ 8
Алгоритм является численно устойчивым, если:
• в процессе вычислений погрешности округления не накапливаются.

№ 9
На графике приведена зависимость вычислительной погрешности некоторого алгоритма δ от порядка сложности задачи n (например, от числа уравнений и неизвестных). В области 1 ошибка σ практически постоянна, в области 2 – слабо возрастает с ростом n, в области 3 – резко возрастает.

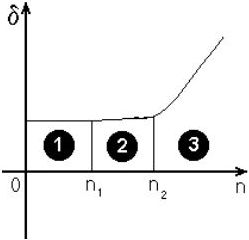
• целесообразно использовать данный алгоритм в области 1 и 2 значений n.

№ 10
Пусть на ЭВМ нужно найти сумму неравных положительных чисел. Ошибка вычисления суммы минимальна, если:
• суммирование производится в порядке возрастания чисел.

№ 1
После выполнения действий с приближенными числами получен результат R=342,714057. Известно, что предельная абсолютная погрешность вычисления R равна Δ=0,02.
• R=342,7

№ 2
Предельные относительные погрешности разности двух чисел a₁=17,9 и a₂=17,7, если абсолютные погрешности этих чисел равны Δ(a₁)=Δ(a₂)=0,05.
• 0,500; 0,004.

№ 3
Абсолютные погрешности произведения двух чисел a₁=2 и a₂=20, если относительные погрешности этих чисел равны 1%.
• 0,800; 0,004.

№ 4
Предельные абсолютные погрешности вычисления площади прямоугольника со сторонами a=3 и b=5, если предельные относительные погрешности измерения a и b равны 1%.
• 0,300; 0,004.

№ 5
Пусть a* - точное значение числа, a – его приближенное значение. Известно, что предельная абсолютная погрешность числа a равна 0,1.
• |a*-a|≤1;
• |a*-a|≤0,1.

№ 6
Пусть приближенное значение числа x равно x=4, a₁=√x, a₂=x². Отношение δ(a₁) / δ(a₂), где δ(a₁) и δ(a₂) - относительные погрешности a₁ и a₂:
• 0,250; 0,004.

№ 7
Пусть на ЭВМ вычисляется сумма двух чисел с=а+b, Δ(a) - абсолютная погрешность округления числа a, Δ(b) - абсолютная погрешность округления числа b, Δ_op(c) - абсолютная погрешность округления результата c.
Абсолютная погрешность результата Δ(c):
• Δ(c)=Δ(a)+Δ(b)+Δ_op(c).

№ 8
Количество верных цифр в узком и широком смысле для приближенного числа а, если известна его предельная абсолютная погрешность Δ(a): a=0,3941; Δ(a)=0,25*10^-2.
• 2 цифры верны в узком смысле, 3 – в широком смысле.

№ 9
Количество верных цифр в узком и широком смысле для приближенного числа а, если известна его предельная относительная погрешность δ(a): a=0,3941; δ(a)=0,1%
• 1 цифра верна и в узком смысле, и в широком смысле.

№ 10
Округлить сомнительные цифры числа а, оставив в нем верные знаки в узком смысле a=47,453±0,024:
• 47,4.

№ 1
Пусть требуется вычислить значение полинома P(x) десятого порядка при некотором значении х. Число операций умножения при вычислении значения P(x) по схеме Горнера:
• 10.

№2
Диапазон изменения x, в котором не произойдет переполнения разрядной сетки ЭВМ при вычислении функции e^x (здесь M₀ - машинный нуль, M_∞ - машинная бесконечность):
• x∈[-M_∞, ln M_∞].

№ 3
Наиболее широкий интервал запрещенных значений при вычислении на ЭВМ функции ln x:
• x[-M_∞, 0].

№ 4
- функции √x:
• x[-M_∞, 0).

№ 5
Относительная погрешность вычисления периметра прямоугольника со сторонами a=3 и b=5, если абсолютные погрешности измерения a и b равны 0,05 (в процентах):
• 1,250; 0,004.

№ 6
После выполнения действий с приближенными числами результат записан в виде R=132,14. Предельная абсолютная погрешность результата:
• 0,005; 0,004.

№ 7
“Машинный нуль” – это:
• наименьшее положительное число, которое может быть представлено в разрядной сетке ЭВМ.

№ 8
Величина “машинного эпсилона” в ЭВМ определяется:
• числом разрядов, отводимых под мантиссу числа.

№ 9
Пусть a₁ и a₂ - приближенные значения двух положительных чисел. Относительная погрешность результата может быть во много раз больше относительной погрешности чисел a₁ и a₂, при:
• вычитании a₁ и a₂.

№ 10
Неверное правило в выполнении арифметических операций в ЭВМ:
• При вычислении на ЭВМ порядок операций и расстановки скобок в арифметических выражениях не влияет на точность результата.

№1
Дана матрица
. Обратная матрица:
• .

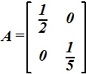№2
Пусть решается система линейных уравнений Ax=b. В результате осуществления прямого хода метода Гаусса получена верхнетреугольная матрица
.
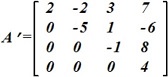Определитель матрицы A в исходной системе уравнений:
• 40.

№3
x = [ 1  -2  5  -8  7 ].
• Для вектора x max-норма ||x_∞=7||.

№4
Число обусловленности системы линейных уравнений, используя 1-норму ||A₁||:

• 25,0; 0,04.

№5
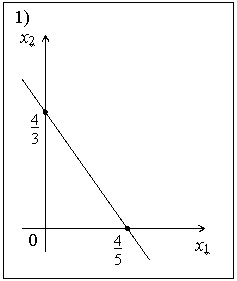
Уравнение 5x₁+3x₂-4=0 соответствует графику
•

№6
Уравнение, соответствующее графику:

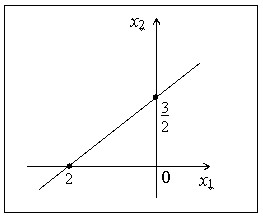
• 1,5x₁-2x₂-3=0.

№7
.
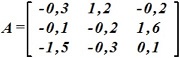• max-норма ||A_∞=1,9||.

№8
.
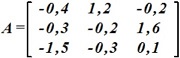• 1-норма ||A₁=2,2||.

№9
Произведение C=A*X, если

:
• .

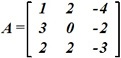
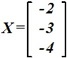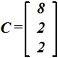№1
Решается система линейных уравнений Ax=b матрицей
.
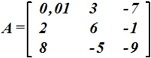Операции, которые необходимо выполнить на первом шаге метода Гаусса с выбором главного элемента в матрице :
• поменять местами строки 1 и 3 и столбцы 1 и 3.

№2
Случай плохо обусловленной системы линейных уравнений с двумя неизвестными:

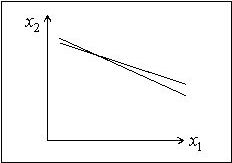
№3
Для матрицы A порядка n методом Гаусса находится обратная матрица. Составить и решить при этом нужно:
• n систем линейных уравнений.

№4
Структура матрицы, для которой применяется метод прогонки (линиями условно показано расположение ненулевых элементов, остальные элементы матрицы равны нулю).

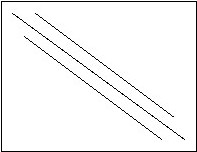
№5
Система линейных уравнений решается методом простых итераций.
.
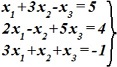• Для этой системы условие сходимости метода не выполняется.

№6
Система линейных уравнений Ax=b решается методом простых итераций.
.
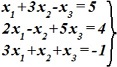Чтобы удовлетворялись условия сходимости метода нужно:
• 1-е уравнение поставить на второе место, 2-е уравнение – на третье место, 3-е уравнение – на первое место.

№7
Дана система линейных уравнений:
.
Каждое из уравнений на плоскости x₁-x₂ может быть представлено некоторой линией. График, который соответствует системе линейных уравнений, имеющей единственное решение:

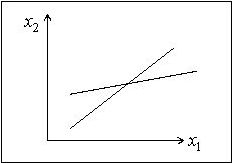
№8
Не накапливает погрешностей за счет ошибки округления:
• метод простой итерации (Якоби).

№9
К наименьшему числу операций приводит метод решения систем линейных уравнений:
• Гаусса.

№10
.
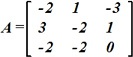• 2-норма ||A₂=6||.

№ 1-3,5
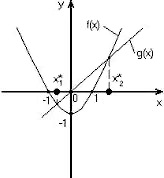
Графическая интерпретация задачи нахождения корней уравнения y=f(x)=0 (на рисунках x*₁ и x*₂ – корни уравнения).
.
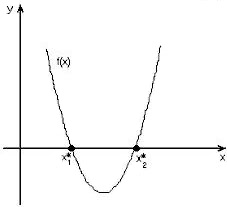f(x)=g(x).
.
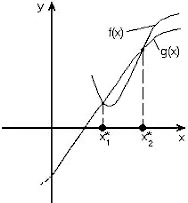y=(x-1)²-1=0.
.
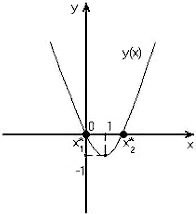f(x)=g(x), f(x)=x²-1, g(x)=x.

№ 4,6
Уравнение f(x)=0, которое соответствует графику.

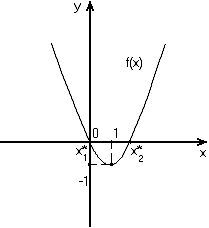
• (x-1)²-1=0.
f(x)=g(x).

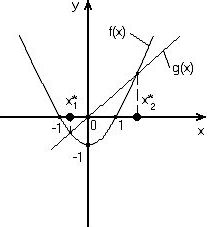
• f(x)=x²-1, g(x)=x.

№ 7-9
Графическая интерпретация одного из методов решения полиномиального уравнения f(x)=0 (x*) - корень уравнения, x_i – последовательные приближения в корень).

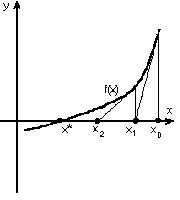
Она соответствует:
• Методу Ньютона.

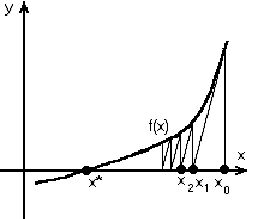
• Модифицированному (упрощенному) методу Ньютона.
- нелинейного уравнения:

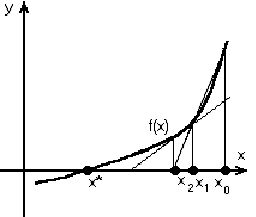
• Методу секущих.

№ 10
Графическая интерпретация задачи нахождения корней системы уравнений:

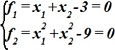
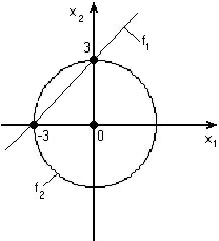
№ 1,2,9
Методом дихотомии (деления отрезка пополам) вычисляют корень уравнения x²-6=0 в интервале [2;3].
Сделать три итерации.
• 2,37; 0,004.
Интервал неопределенности (т.е. интервал, содержащий корень) после пяти итераций:
• 2⁵ или 32 раза.
- корень уравнения x²-15=0 в интервале [3; 4]. Сделать три итерации.
• 3,87; 0,004.

№ 3-5
Уточнить корень уравнения x²-6=0 методом Ньютона. Сделать три итерации, в качестве начальной взять точку x₀=2.
• 2,44; 0,004.
- модифицированным (упрощенным) методом Ньютона.
• 2,45; 0,004.
- методом секущих. Сделать две итерации, в качестве начальных - точки x₀=1,5; x₁=2.
• 2,43; 0,004.

№ 6
Дана система уравнений:
.
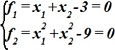Якобиан (определитель матрицы Якоби) в точке x₁=2, x₂=1:
• -2.

№ 7,8,10
Пусть модифицированным (упрощенным) методом Ньютона уточняется корень уравнения x²-6=0 из начальной точки x₀=2. Формула для выполнения итераций:
• x_k+1=1,5+x_k-(x²_k/4).
- методом Ньютона:
• x_k+1=1/2 (x_k+6/x_k).
- методом секущих:
• x_k+1=(x_k-x_k²-6)/(x_k+x_k-1).

№ 1-3
Функция f(x) на интервале x∈[a;b] приближается функцией θ(x).
Критерий близости f и θ, представленный на рисунке:

• .
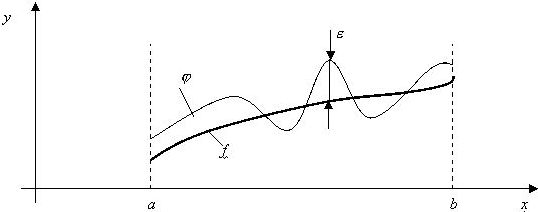
Критерий близости ε функций f и θ:

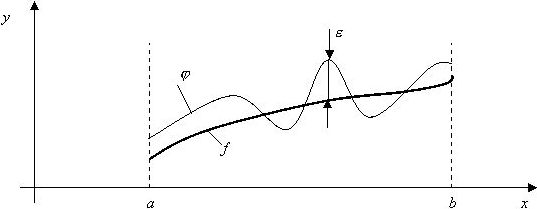
• метод наилучшей равномерной аппроксимации.
Метод аппроксимации функции θ(x) в заранее указанных точках x_i∈[a;b] (i=0,n), совпадающий с f(x), т.е. θ(x_i)=f(x_i), i=0,n:
• интерполяция.

№ 4
Функция f(x) интерполируется полиномом n-го порядка P_n(x)=a₀+a₁x+...+a_nx_n.
Для нахождения полинома P_n(x) необходимо взять узлов интерполяции:
• m=n+1.

№ 5
Функция f(x), заданная своими значениями в 100 точках интервала x∈[a;b], приближается по методу наименьших квадратов линейной функцией P(x)=C₀+C₁*x.
Для нахождения P(x) необходимо составить:
• 2 уравнения.

№ 6
На плоскости заданы четыре точки с координатами (x₁,y₁), (x₂,y₂), (x₃,y₃), (x₄,y₄), причем (x₁<x₂<x₃<x₄).
Кривая, описываемая формулой f(x)=a₀+a₁x+a₂x²+a₃x³ и проходящая одновременно через все эти точки существует:
• одна.

№ 7,9
Функция f(x) на интервале x∈[a;b] приближается функцией θ(x).
Критерий близости ε функций f и θ: ε=∫(f(x)-θ(x)) ² dx,a,b применяется в
• методе наименьших квадратов.

• наилучшая равномерная аппроксимация.

№ 8
Экспериментально измерена зависимость температуры T нити накаливания лампы от приложенного напряжения U. Нужно по этим данным найти аналитическую формулу, описывающую зависимость T(U) в виде полинома. Чтобы уменьшить влияние случайных ошибок измерения целесообразно использовать:
• метод наименьших квадратов.

№ 1
Функция y=ε^x в точках, равномерно расположенных на интервале x∈[-1;1], интерполируется полиномом n-го порядка P_n(x)=a₀+a₀x+...+a_nxⁿ.
Ошибка интерполяции при возрастании n:
• уменьшается.

№ 2,4,7
Функция f(x) в точках x_i (i=0,n) интерполируется кубическим сплайном. При этом используется:
• n полиномов 3-го порядка.
Не используются при формировании уравнений для нахождения коэффициентов сплайна:
• третья производная сплайна в точках “стыка” x_i (i=1,n-1) непрерывна;
• первая производная сплайна в начальной (x₀) и конечной (x_n) точках равна заданному значению;
• третья производная сплайна в начальной (x₀) и конечной (x_n) точках равна заданному значению.
- в 5 точках x_i (i=0,4):
• четыре полинома 3-го порядка.

№ 3
Уменьшить влияние случайных ошибок в исходных данных позволяет:
• метод наименьших квадратов.

№ 5
Функция f(x) в 5 точках интерполируется кубическим сплайном. Необходимо найти:
• 16 неизвестных коэффициентов сплайна.

№ 6

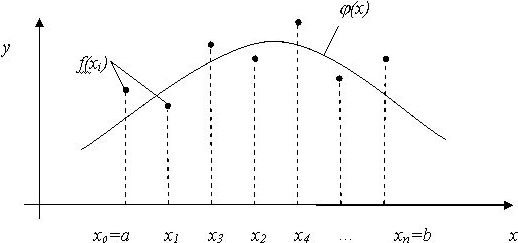
На рисунке показаны значения функции f(x), заданные в дискретных точках x_i (i=0,n) на интервале [a;b], и график приближающей функции θ(x). Метод приближения, соответствующий рисунку:
• наименьших квадратов.

№ 8,9
Функция f(x) в 6 точках интерполируется кубическим сплайном. Необходимо найти:
• 20 неизвестных коэффициентов сплайна.
в 4 точках:
• 12.

№ 10
На плоскости заданы пять точек с координатами (x₁,y₁), (x₂,y₂), ..., (x₅,y₅), причем (x₁<x₂<x₃<x₄<x₅).
Существует кривых, описываемых формулой f(x)=a₀+a₁x+a₂x²+a₃x³+a₄x⁴ и проходящих одновременно через все эти точки:
• одна.

№ 1,4,6,8,10
Метод наименьших квадратов. Функция y=f(x), заданная табличными значениями, приближается функцией θ(x)=C₀+C^x₁.

x	-1	0	1	2
y	0,01	0,1	1	10

• C₀=0,100±0,05; C₁=1,00±0,05.
θ(x)=C₀+C₁/x.

x	1	2	4
y	3	2	1,5

• C₀=2,000±0,4; C₁=1,000±0,4.
θ(x)=C₀+C₁x.

x	1	2	3
y	4	6	8

• C₀=2,000±0,4; C₁=2,000±0,4.
θ(x)=C₀+C₁lgx.

x	0,01	0,1	1	10
y	1	2	3	4

• C₀=3,00±0,04; C₁=1,00±0,04.
θ(x)=C₀x^C1.

x	10	1	0,1	0,01
y	0,01	0,1	1	10

• C₀=0,100±0,04; C₁=-1,00±0,04.

№ 2,3,5,7
Абсолютная ошибка интерполяции в точке x=1,5 функции y=lnx полиномом P(x) первой степени на отрезке [1;2], если в качестве узлов используются концы отрезка:
• 0,125; 0,0004.
x=0,5. y=ε^x на отрезке [0;1]:
• 0,339; 0,0004.
x=0,5. y=ε^-x на отрезке [0;1]:
• 0,422; 0,0004.
x=0,5. y=xε^-x на отрезке [0;1]:
• 0,119; 0,0004.

№ 9
Функция y=√x интерполируется полиномом P(x) в точках x=100;121;144. С помощью полинома можно вычислить √117 с точностью:
• 0,00115; 0,000004.

№ 1,2
Функция y=f(x) задана таблицей.

x	0,00	0,10	0,20
y	0,00000	0,20134	0,41075

В точке x=0,10 значения f´(x) по формулам левой, правой и центральной разностных производных:
• 2,0134±0,00004; 2,0941±0,00004; 2,0537±0,00004.
В точке x=0,10 найти f´´(x):
• 0,807; 0,0004.

№ 3,4
Функция y=sinx.

x	1,01	1,02	1,03
sinx	0,8468	0,8521	0,8573

В точке x=1,02 значения f´(x) по формулам левой, правой и центральной разностных производных:
• 0,530±0,004; 0,520±0,004; 0,525±0,0004.
В точке x=1,02 f´´(x) по формуле центральной разностной производной:
• -1,00; 0,04.

№ 5

x	1,01	1,02	1,03
sinx	0,8468	0,8521	0,8573

В точке x=1,02 значения f´(x) по формуле центральной разностной производной, ошибка вычисления производной:
• 0,525±0,0004; 0,00000858±0,000000004.

№ 6

x	1,02	1,03	1,04
sinx	0,8521	0,8573	0,8624

В точке x=1,03 f´´(x) по формуле центральной разностной производной, ошибка вычисления второй производной:
• -1,00±0,04; 0,00506±0,000004.

№ 7

x	1,00	1,01	1,02	1,03	1,04
sinx	0,8415	8,8468	0,8521	0,8573	0,8624

В точке x=1,02 значения f´(x) с помощью интерполяции по пяти узлам, ошибка вычисления производной:
• 0,525±0,0004; 2,874*10^-10.

№ 8-10
Дан полином P(x)=3x²-2x-1. P´(x) по формулам левой, правой и центральной разностной производной при x=2 (шаг h=0,1):
• 9,700±0,04; 10,300±0,04; 10,000±0,04.
P´´(x) по формуле центральной разностной производной. Ошибка вычисления производной:
• 5,999±0,0004; 0,000.
P´(x) с помощью интерполяции по пяти узлам:
• 10,0666±0,00004; 0,000.

№ 1-3
Вычислить интеграл

по формуле прямоугольников, число интервалов взять равным n=2. Оценить погрешность вычисления интеграла:
• 0,0200±0,004; 0,000666±0,0000004.
- по формуле трапеций:
• 0,0240±0,0004; 0,00133±0,000004.
- по формуле Симпсона:
• 0,0213±0,00004; 0,00.

№ 4-8
:
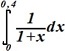• 0,335±0,0004; 0,00133±0,000004.
:
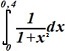• 0,381±0,0004; 0,000333±0,0000004.
:
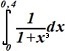• 0,335±0,0004; 0,001503±0,00004.
:
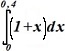• 0,480±0,004; 0,00.
:
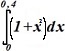• 0,420±0,004; 0,00133±0,000004.

№ 9,10
Оценить, с какой точностью по формуле прямоугольников можно вычислить интеграл
,
используя 5 значений подынтегральной функции (n=4).
• 0,00707; 0,000004.
- по формуле трапеций:
• 0,0141; 0,00004.