5.2 Амплитудная модуляция

В процессе амплитудной модуляции амплитуда U₀ несущего колебания u₀ (t) = U₀ cos(ωt+φ) перестает быть постоянной и изменяется по закону передаваемого сообщения. Амплитуда U(t) несущего колебания может быть связана с передаваемым сообщением соотношением:

U(t) = U₀ + k_A e(t),    (5.1)

где U₀ - амплитуда несущего колебания в отсутствии сообщения (немодулированное колебание); e(t) - функция, зависящая от времени, соответствующая передаваемому сообщению (ее называют модулирующим сигналом); k_A - коэффициент пропорциональности, отражающий степень влияния модулирующего сигнала на величину изменения амплитуды результирующего сигнала (модулированного колебания).

Выражение для амплитудно-модулированного сигнала в общем случае имеет вид:

u_АМ(t) = [U₀ + k_A e(t)] cos(ω₀t+φ).    (5.2)

Простейший для анализа случай амплитудно-модулированного колебания получается, если в качестве модулирующего сигнала используется гармоническое колебание (такой случай называется тональной модуляцией):

e(t) = E cos(´Ωt+Θ),    (5.3)

где Е - амплитуда, ´Ω - угловая частота; Θ - начальная фаза модулирующего сигнала.

Для упрощения анализа будем полагать начальные фазы колебаний равными нулю, что не повлияет на общность выводов. Тогда для тональной амплитудной модуляции можно записать:

u_АМ(t) = [U₀ + k_A E cos´Ωt] cosω₀t = U₀ [1+ M_A cos´Ωt] cosω₀t,    (5.4)

где М_A = Е/U₀ - коэффициент амплитудной модуляции (иногда говорят - глубина амплитудной модуляции).

Для определения спектра амплитудно-модулированного колебания выполним несложные преобразования выражения (5.4):

u_АМ(t) =U₀ cosω₀t + U₀ M_A cos´Ωt cosω₀t = U₀ cosω₀t + (U₀ M_A/2) cos(ω₀ - ´Ω)t + (U₀ M_A/2) cos(ω₀ + ´Ω)t.    (5.5)

Из анализа выражения (5.5) следует, что при амплитудной модуляции гармоническим колебанием спектр амплитудно-модулированного сигнала содержит три гармонические составляющие. Гармоническая составляющая с частотой, равной ω₀, представляет собой исходную немодулированную несущую с частотой ω₀ и амплитудой U₀.

Гармонические составляющие с частотами, равными (ω₀ - ´Ω) и (ω₀ + ´Ω) представляют собой продукт амплитудной модуляции и называются, соответственно, нижней и верхней боковыми составляющими. Амплитуды боковых составляющих одинаковы, равны U₀ M_A/2 и расположены симметрично относительно несущей частоты ω₀ на расстоянии, равном - ´Ω. Таким образом, ширина полосы частот Δω, занимаемая амплитудно-модулированным колебанием при модуляции гармоническим сигналом с частотой ´Ω, равна Δω =2´Ω.

Графики несущего колебания u₀(t), модулирующего сигнала е(t) и амплитудно-модулированного сигнала u_АМ(t) приведены на рисунке 5.1.

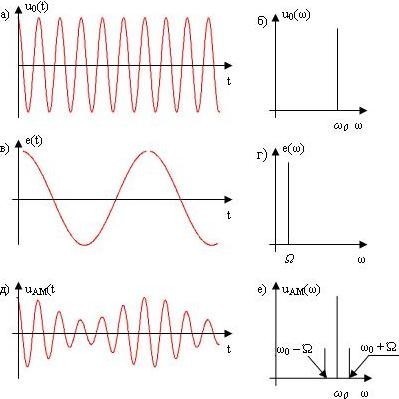
Рис. 5.1  Тональная амплитудная модуляция:
а) несущее колебание и его спектр (б);
в) модулирующий сигнал и его спектр (г);
д) амплитудно-модулированное колебание и его спектр (е)

При отсутствии модуляции (М_A = 0) амплитуды боковых составляющих равны нулю и спектр амплитудно-модулированного сигнала состоит только из несущего колебания с частотой ω₀. При коэффициенте амплитудной модуляции М_A < 1 амплитуда результирующего колебания изменяется от максимального значения U_MAX = U₀(1 + M_A) до минимального U_MIN = U₀(1 - M_A).

Таким образом, коэффициент М_A амплитудной модуляции может быть определен как

М_A = (U_MAX - U_MIN)/(U_MAX + U_MIN).    (5.6)

При коэффициенте амплитудной модуляции М_A >1 возникают искажения, называемые перемодуляцией (рисунок 5.2). Такие искажения могут приводить к потере информации и их стараются не допускать.

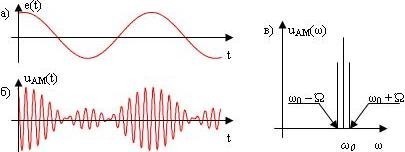
Рис. 5.2 Тональная амплитудная модуляция при коэффициенте М_A > 1:
а) модулирующий сигнал; б) амплитудно-модулированное колебание и его спектр (в)

Подобный подход можно применить и к анализу амплитудно-модулированных колебаний сложной формы. В этом случае периодический модулирующий сигнал может быть представлен набором гармонических составляющих, частота которых кратна периоду исходного сигнала. Каждая из гармоник модулирующего сигнала сформирует в спектре амплитудно-модулированного колебания две боковые составляющие, симметрично отстоящие от несущей на величину, равную частоте соответствующей гармоники. Для примера, если спектр модулирующего сигнала имеет вид, представленный на рисунке 5.3,а, то спектр амплитудно-модулированного колебания может быть представлен диаграммой, приведенной на рисунке 5.3,б.

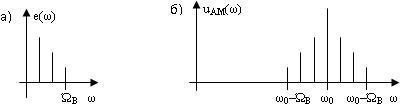
Рис. 5.3 Спектры сигналов: а) модулирующего сигнала; б) амплитудно-модулированного колебания

В общем случае, ширина П_АМ спектра амплитудно-модулированного колебания равна

П_АМ = 2 ´Ω_В,    (5.7)

где ´Ω_В верхняя (наибольшая) частота в спектре модулирующего сигнала.