Эконометрика
Специальность 351400
Лузина Л.И.
Томск-2001

№ 1
Экономической называется модель:
• Математическая модель, описывающая механизм функционирования гипотетической экономической или социально-экономической системы.

№ 2
Эконометрическая:
• Вероятностно-статистическая модель, описывающая механизм функционирования экономической или социально-экономической системы.

№ 3
Чтобы “паутинная” модель превратилась из экономической в эконометрическую:
• Следует говорить о конкретном действии закона.

№ 4
Суть эконометрики:
• В синтезе экономики, экономической статистики и математики.

№ 5
Главное назначение эконометрики:
• Модельное описание конкретных количественных взаимосвязей, существующих между показателями.

№ 6
Можно расклассифицировать задачи, которые решаются с помощью эконометрики по:
• конечным прикладным целям.
• уровню иерархии.
• профилю анализируемой экономической системы.

№ 7
Уровни иерархии анализируемой экономической системы:
• Макроуровень, мезоуровень и микроуровень.

№ 8
Уровни иерархии:
• Макроуровень - страны в целом; мезоуровень - регионы, отрасли; микроуровень - семьи, предприятия, фирмы.

№ 9
Конечные прикладные цели в задачах, которые решаются в эконометрике:
• Прогноз экономических показателей и имитация различных возможных сценариев социально-экономического развития.

№ 10
Определен профиль эконометрического моделирования:
• Исследование сконцентрировано на каких-то проблемах рынка, инвестиционной, финансовой или социальной политики, ценообразования, спроса и потребления или на определенном комплексе проблем.

№ 11
Отличие вероятностно-статистическая модели от вероятностной:
• Значения отдельных характеристик вероятностно-статистической модели оцениваются по результатам наблюдений, характеризующим функционирование моделируемого конкретного явления.

№ 12
Вероятностная модель не имитирует механизм функционирования конкретного реального явления.

№ 13
Точка пересечения кривых спроса и предложения является точкой равновесия “паутинной” модели.

№ 14
Термин “Эконометрика” означает:
• Измерения в экономике.

№ 15
Математическая экономика становится эконометрикой:
• Когда представленные в этих взаимосвязях коэффициенты заменяются конкретными числовыми оценками, полученными на базе экономических данных.

№ 16
Форма представления стохастической зависимости, которая является распространенной в эконометрике:
• Аддитивная линейная форма.

№ 17
Случайная составляющая в аддитивной форме характеризует:
• Разницу между модельным и наблюденным значениями.

№ 18
Под модельным значением результирующей переменной понимают значение результирующей переменной, восстановленное по заданным величинам объясняющих переменных при условии известных коэффициентов.

№ 19
Переменные, участвующие в эконометрической модели, делятся на:
• Экзогенные, эндогенные и предопределенные.

№ 20
Задаются как бы “извне”:
• Экзогенные переменные.

№ 21
Под лаговыми эндогенными переменными понимают:
• Эндогенные переменные, значения которых входят в уравнения измеренными в прошлые моменты времени.

№ 22
Множество предопределенных переменных формируется:
• Из всех экзогенных и лаговых эндогенных переменных.

№ 23
Формы эконометрической модели:
• Структурная и приведенная.

№ 24
Идентификация модели:
• Статистический анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели.

№ 25
Причины присутствия случайной составляющей (“регрессионных остатков”):
• Случайная составляющая отражает влияние на формирование значений у факторов, не учтенных в перечне объясняющих переменных X; случайная составляющая может включать в себя случайную погрешность в измерении значения результирующего показателя Y.

№ 26
Данные в регрессионном анализе представляют:
• В виде двух матриц Х размера n x (P+1), составленных из наблюденных значений объясняющих переменных, и матрицы Y размера n x 1, составленной из наблюденных значений результирующей переменной.

№ 27
Существуют выборки:
• Пространственные, временные и пространственно-временные.

№ 28
В рамках классической линейной модели множественной регрессии рассматриваются:
• Линейные функции регрессии.

№ 29
В классической линейной модели множественной регрессии предполагается взаимная некоррелированность случайных регрессионных остатков.

№ 30
Гомоскедастичность регрессионных остатков:
• Постоянство, независимость дисперсий остатков σ² от номера наблюдения i.

№ 31
Требование rank(X)=p+1<n означает, что:
• Не должно существовать строгой линейной зависимости между объясняющими переменными. Если одна объясняющая переменная может быть линейно выражена через какое-то количество других, то ранг матрицы X окажется меньше p+1.

№ 32
Y и X связаны нормальной классической линейной моделью множественной регрессии (КЛММР):
• Когда к требованиям КЛММР дополнительно предполагается нормальный характер распределения регрессионных остатков #math epsilon.

№ 33
Методы для оценивания неизвестных параметров нормальной классической линейной модели множественной регрессии:
• наименьших квадратов.
• максимального правдоподобия.

№ 34
В основе метода наименьших квадратов (МНК) лежит:
• стремление исследователя подобрать такие оценки ϑ^{^}₀, ϑ^{^}₁, ..., ϑ^{^}_p для неизвестных значений параметров функции регрессии соответственно ϑ₀, ϑ₁, ..., ϑ_p при которых регрессионные значения ϑ^{^}₀ + ϑ^{^}₁x^(l)_i + ... + ϑ^{^}_px^(p)_i результирующего показателя как можно меньше отличались бы от соответствующих наблюденных значений y_i.

№ 35
Под “невязками” ε^{^}_i понимают:
• меру расхождения регрессионного и наблюденного в i-том наблюдении значений результирующего показателя разность.

№ 36
Оценки по методу наименьших квадратов:
• подбираются таким образом, чтобы минимизировать критерий.

№ 37
Парной линейной регрессией называют случай:
• когда рассматривается зависимость у от единственной объясняющей переменной, т.е. р=1.

№ 38
Основная формула метода наименьших квадратов:
• .

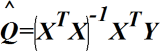№ 39
При использовании метода максимального правдоподобия находятся:
• оценки неизвестных параметров и дисперсии

№ 40
Оценки максимального правдоподобия находятся:
• из условия, при котором функция правдоподобия или логарифмическая функция правдоподобия достигает своей максимальной величины.

№ 41
Оценки параметров, полученные по МНК и ММП, совпадают.

№ 42
Оценки являются состоятельными:
• когда наименьшее собственное значение матрицы X^TX стремится к бесконечности при n → ∞.

№ 43
Оценка Q' параметра Q называется несмещенной:
• для которой выполняется равенство MQ'=Q.

№ 44
МНК - оценки параметров являются несмещенными (МНК - метод наименьших квадратов).

№ 45
ММП - несмещенными.

№ 46
Можно получить несмещенную оценку неизвестной дисперсии остатков.

№ 47
Диагональные элементы ковариационной матрицы вектора МНК - оценок задают:
• средние квадраты ошибок соответствующих оценок, а для несмещенных оценок задают дисперсии оценок.

№ 48
Решающей характеристикой качества оценки неизвестного числового параметра Q является:
• средний квадрат ошибки M(-Q)².

№ 49
Оценка Q^{^}₁ лучше (эффективнее), если средний квадрат ошибки оценки Q^{^}₁ меньше среднего квадрата ошибки оценки Q^{^}₂.

№ 50
При моделировании реальных экономических процессов возможны ситуации, в которых условиях классической линейной модели оказываются нарушенными.

№ 51
На практике часто становится нереалистичным:
• Условие взаимной некоррелированности и гомоскедастичности регрессионных остатков.

№ 52
Условие некоррелированности и гомоскедастичности регрессионных остатков выражается соотношением:
• дисперсия умножается на единичную матрицу размеров nхn, где n - объем выборки.

№ 53
Формальная запись ОЛММР от КЛММР отличается:
• только отказом от требования некоррелированности и гомоскедастичности регрессионных остатков.

№ 54
Ковариационная матрица регрессионных остатков в ОЛММР:
• Дисперсия умножается на симметричную положительно определенную матрицу.

№ 55,56
В соотношении ковариационной матрицы регрессионных остатков в ОЛММР дисперсия σ² не известна, симметричная матрица известна.

№ 57
То, что симметричная матрица известна, не является реалистичным предположением.

№ 58
ОЛММР описывается:
• Системой соотношений и условий.

№ 59
ОЛММР от КЛММР отличается:
• Только видом ковариационной матрицы.

№ 60
Под гетероскедастичными регрессионными остатками (РО) понимаются:
• РО, которые не отвечают требованиям гомоскедастичности.

№ 61
В ситуациях, когда исходные наблюдения регистрируются во времени, регрессионные остатки являются статистически взаимосвязанными.

№ 62
Не может быть диагональной ковариационная матрица регрессионных остатков в случае, когда эти остатки являются статистически взаимосвязанными.

№ 63
Природа зависимости регрессионных остатков в случае, когда исходные наблюдения регистрируются во времени:
• Эта зависимость ослабевает по мере их взаимного удаления друг от друга во времени.

№ 64
Корреляционная связь между регрессионными остатками зависит:
• Только от меры их “разнесенности” во времени.

№ 65
Корреляционная связь между регрессионными остатками не зависит от того, к каким именно моментам времени они “привязаны”.

№ 66
Корреляционная связь между регрессионными остатками, при неограниченном удалении их друг от друга во времени, исчезает вовсе.

№ 67,68
В рамках ОЛММР МНК оценки параметров остаются состоятельными, несмещенными.

№ 69
МНК - оценки параметров в условиях ОЛММР не являются оптимальными.

№ 70
Оценки параметров по обобщенному методу наименьших квадратов определяются другим соотношением, чем МНК - оценки.

№ 71
Ковариационная матрица оценок - ОМНК определяется другим соотношением, чем ковариационная матрица МНК - оценок.

№ 72
Ковариационная матрица регрессионных остатков в большинстве ситуаций практики эконометрического моделирования заранее не известна.

№ 73
Выражение “задана структура ковариационной матрицы регрессионных остатков” означает, что:
• ковариационная матрица рассматривается как функция известного вида от неизвестных параметров.

№ 74
Коэффициенты эластичности являются важным инструментом экономического анализа.

№ 75
Коэффициенты эластичности определяются на базе:
• анализа функциональных зависимостей, существующих между некоторой интересующей нас экономической характеристикой z и набором объясняющих переменных u.

№ 76
Коэффициент эластичности определяется как:
• логарифмическая производная результирующего показателя z по объясняющей переменной u.

№ 77
Коэффициент эластичности:
• определяет на сколько процентов изменится значение результирующего показателя z при изменении объясняющей переменной на 1 %.

№ 78
В экономике существуют:
• Линейные и нелинейные связи.

№ 79
Производственная функция (зависимости, существующие между объемом производственной продукции и основными факторами производства) является нелинейной функцией.

№ 80
Функция спроса (зависимости, существующие между спросом на какой-либо вид товаров и доходом и ценами на этот и другие товары) является нелинейной функцией.

№ 81
Под процедурой линеаризацией модели понимают:
• Когда связь между Y и Х представлена в виде линейной функции регрессии.

№ 82
Линеаризовать модель не всегда возможно.

№ 83
Виды нелинейных зависимостей, поддающиеся линеаризации:
• гиперболического типа.
• показательного типа.
• степенного типа.
• логарифмического типа.

№ 84
Если анализируемые переменные и регрессионные остатки связаны между собой зависимостью гиперболического типа:
• Кривая регрессии характеризуется двумя асимптотами - горизонтальной (y=ϑ₀) и вертикальной (х=0).

№ 85
Зависимость гиперболического типа y=ϑ₀+ϑ₁/x+ε, 0<x<∞, приводится к линейному виду:
• С помощью преобразования переменной =1/x.

№ 86
Если имеем зависимость вида y=1/(ϑ₀+ϑ₁x+ε), -(ϑ₀/ϑ₁)<x<∞ в качестве результирующего признака необходимо рассмотреть переменную:
• =1/y.

№ 87
Если имеем зависимость вида y=x/(ϑ₀x+ϑ₁+xε), -(ϑ₁/ϑ₀)<x<∞ необходимо перейти к новым переменным:
• =1/y, =1/x.

№ 88
Кривые Энгеля описывают:
• Зависимость спроса на определенный вид товаров от уровня доходов потребителей.

№ 89
Свести зависимость показательного типа y=ϑ₀e^ϑ1x+ε к линейному виду, позволяет переход к новой переменной:
• y'=ln(y).

№ 90
Зависимость y=ϑ₀e^ϑ1/x+ε можно свести к линейному виду с помощью преобразований переменных:
• y'=ln(y), x'=1/x.

№ 91
Логистические кривые используются:
• Для описания поведения показателей, имеющих определенные “уровня насыщения”.

№ 92
Можно использовать логистические кривые для описания зависимости спроса на товар от дохода.

№ 93
Степенные зависимости при построении и анализе функций спроса использовать можно.

№ 94
Зависимости степенного типа можно свести к линейному виду с помощью переменных:
• y'=ln(y), x'=ln(x).

№ 95
Если эластичность Y по каждой из объясняющих переменных X постоянна, то Y и Х могут быть связаны только зависимостью степенного типа:
• Да.

№ 96
Зависимость логарифмического типа можно свести к линейному виду с помощью переменной:
• x'=ln(x).

№ 97
Приходим к нелинейной функции регрессии:
• Подобрать такие преобразования переменных, которые позволили бы представить зависимость в виде линейного соотношения.

№ 98
Если невозможно линеаризовать модель:
• Исследовать нелинейную зависимость в терминах исходных переменных.

№ 99
Асимптоты логистической кривой:
• Две горизонтальные асимптоты y=0 и y=1/ϑ₀.

№ 100
Логистическая кривая имеет “точку перегиба”:
• x₀=ln(ϑ₁/ϑ₀); y₀=1/(2ϑ₀).