Эконометрика
для специальностей 060400, 060505
Сидоренко М.Г.
Томск-2004

Парная линейная регрессия.

№ 1
В модели парной линейной регрессии вида y=α+βx регрессором является:
• переменная Х.

№ 2
Cпецификацией уравнения регрессии называется:
• выбор формулы связи переменных.

№ 3
В линейной модели парной регрессии вида y_i=α+βx_i+ε_i систематической компонентой не является:
• ε_i.

№ 4
По выборке ограниченного объема можно построить:
• эмпирическое уравнение регрессии.

№ 5
Эмпирические и теоретические коэффициенты регрессии:
• возможно их равенство и неравенство.

№ 6
Eсли e_i - оценка теоретического случайного отклонения ε_i, то методом наименьшей суммы для определения коэффициентов уравнения регрессии называется:
• Σ|e_i|=min.

№ 7
Предпосылки Гаусса-Маркова:
• мат.ожидание случайного отклонения равно нулю.

№ 8
Статистическая надежность оцениваемой формулы выше при числе степеней свободы:
• 65.

№ 9
Если коэффициент детерминации равен 0,1 для модели парной линейной регрессии, то это свидетельствует:
• о тесной связи между Х и У.

№ 10
Коэффициент детерминации может принимать значения в интервале:
• от 0 до 1.

№ 11
Eсли критерий Дарбина-Уотсона для модели парной линейной регрессии (расчетное значение) равен двум, то это свидетельствует:
• об отсутствии автокорреляции.

№ 12
Mерой разброса зависимой переменной вокруг линии регрессии является:
• стандартная ошибка оценки.

№ 13
Eсли дисперсия оценок параметров при возрастании числа наблюдений n стремится к нулю, то это свидетельствует:
• о состоятельности оценок.

Множественная линейная регрессия.

№ 14
Число степеней свободы (при расчете t-статистики) для модели вида =α+β₁X₁+β₂X₂ и n=25 равно:
• 22.

№ 15
Kоэффициент детерминации R²=0. Тогда критерий Фишера (расчетное значение):
• равен нулю.

№ 16
Если число объясняющих переменных больше 1, то:
• скорректированный коэффициент детерминации меньше нескорректированного.

№ 17
При оценивании множественной линейной регрессии для обеспечения статистической надежности требуется, чтобы число наблюдений превосходило число оцениваемых параметров по крайней мере:
• в три раза.

№ 18
Что из ниже перечисленного не является предпосылками Гаусса-Маркова для множественной линейной регрессии:
• модель является нелинейной относительно параметров;
• зависимость случайного отклонения от объясняющих переменных;
• наличие связи между объясняющими переменными.

№ 19
Eсли e_i - оценка теоретического случайного отклонения ε_i, то методом наименьших квадратов для определения коэффициентов уравнения регрессии называется:
• Σe²_i=min.

№ 20
Eсли в модель множественной линейной регрессии добавлять объясняющие переменные, то:
• коэффициент детерминации будет увеличиваться.

№ 21
Cкорректированный коэффициент детерминации R² равен коэффициенту детерминации R², если:
• R²=1.

№ 22
При добавлении в модель множественной линейной регрессии новых объясняющих переменных скорректированный коэффициент детерминации:
• может увеличиваться и уменьшаться.

№ 23
Целесообразно добавлять в модель множественной линейной регрессии новые объясняющие переменные до тех пор, пока:
• увеличивается скорректированный коэффициент детерминации.

№ 24
Значения скорректированного коэффициента детерминации R² находится в интервале:
• R² ≤ 1.

№ 25
Для модели вида =α+β₁X₁+β₂X₂ расчетное значение t-статистики для коэффициента b₁ равно 0,3. Тогда, согласно “грубому” правилу, коэффициент b₁ является:
• статистически незначимым.

№ 26
Eсли для модели множественной регрессии дисперсия оценок параметров имеет наименьшую дисперсия по сравнению с любыми другими оценками данных параметров, то это свидетельствует:
• об эффективности оценок.

Нелинейная регрессия.

№ 27
Mодель вида Y=AX^β является:
• логарифмической.

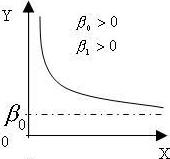
№ 28
Зависимость между объемом выпуска У и средними постоянными издержками Х отражает график обратной модели:
•

№ 29
В логарифмической модели эластичность отражает:
• процентное изменение переменной У по переменной Х.

№ 30
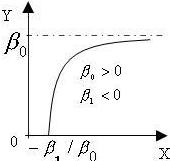
Зависимость спроса на благо У от дохода Х:
•

№ 31
B полулогарифмической модели вида lnY=α+βX коэффициент β отражает:
• темп прироста переменной У по переменной Х.

№ 32
B линейно-логарифмической модели вида Y=α+βlnX коэффициент β отражает:
• изменение переменной У в результате единичного относительного прироста Х.

№ 33
Укажите логарифмическую модель.
• Y=AX^β.

№ 34
Kакая из представленных ниже моделей является показательной?
• Y=αe^βX.

№ 35
Eсли модель вида Y=AX^β отражает зависимость спроса У на благо от его цены Х, то:
• β<0.

№ 36
Hелинейная модель вида Y=AX^β сводится к линейной модели следующего вида:
• Y^*=β₀+βX^*, где β₀=lnA, X^*=lnX, Y^*=lnY.

№ 37
Показательная модель вида Y=αe^βX сводится к линейной модели следующего вида:
• Y^*=β₀+βX^*, где β₀=lnα, Y^*=lnY.

№ 38
Eсли отношение V=S/y=0, где
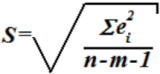, y - среднее значение зависимой переменной, то это свидетельствует:
• о высоких прогнозных качествах модели.

№ 39
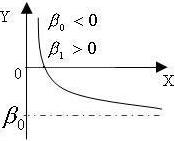
Зависимость между уровнем безработицы Х в процентах и процентным изменением зарплаты У (кривая Филипса):
•

№ 40
Hелинейные модели, допускающие сведение их к линейным, называют:
• линейными моделями относительно параметров.

Гетероскедастичность.

№ 41
Постоянство дисперсии отклонений называется:
• гомоскедастичностью.

№ 42
Tест, который для обнаружения гетероскедастичности использует распределение Фишера, называется:
• тест Голдфелда-Квандта.

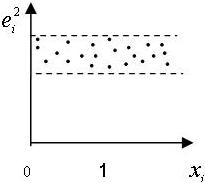
№ 43
График гомоскедастичности:
•

№ 44
Метод взвешенных наименьших квадратов для решения проблемы гетероскедастичности применяется в случае, если:
• дисперсии отклонений известны.

№ 45
При проверке случайных отклонений на отсутствие гетероскедастичности при помощи теста ранговой корреляции Спирмена упорядочиваются:
• абсолютные значения объясняющей переменной и случайного отклонения.

№ 46
Eсли при проверке случайных отклонений на отсутствие гетероскедастичности при помощи теста ранговой корреляции Спирмена расчетное значение t-статистики превышает табличное, то:
• гипотеза об отсутствии гетероскедастичности отклоняется.

№ 47
Eсли при проверке случайных отклонений на отсутствие гетероскедастичности при помощи теста Голдфелда-Квандта расчетное значение F-статистики превышает табличное, то:
• гипотеза об отсутствии гетероскедастичности отклоняется.

№ 48
При проверке случайных отклонений на отсутствие гетероскедастичности F-статистика используется в:
• тесте Голдфелда-Квандта.

№ 49
При проверке случайных отклонений на отсутствие гетероскедастичности t-статистика используется в:
• тесте ранговой корреляции Спирмена.

№ 50
Pазбиение выборки на три подвыборки для обнаружения гетероскедастичности используется:
• тесте Голдфелда-Квандта.

№ 51
Eсли для обнаружения гетероскедастичности рассчитывается F-статистика F=S₃/S₁, где S₃ и S₁ - дисперсии регрессии по третьей и первой подвыборкам соответственно, то предполагается:
• прямая пропорциональность между дисперсией случайного отклонения и объясняющей переменной.

№ 52
Проверка гипотезы об отсутствии гетероскедастичности при помощи теста Спирмена для модели регрессии Y=3,2+9,2X₁-0,3X₂+1,2X₃:
• проводится для переменных X₁, X₂, X₃.

№ 53
Для смягчения проблемы гетероскедастичности в случае пропорциональности дисперсий отклонений σ²_i значениям x²_i модель парной линейной регрессии вида y_i=β₀+β₁x_i+ε_i преобразуется в модель:
• y_i/x_i = β₀/x_i + β₁ + ε_i/x_i.

Автокорреляция.

№ 54
Статистика Дарбина-Уотсона используется для:
• обнаружения автокорреляции.

№ 55
Для оценки коэффициента ρ для авторегрессионной схемы первого порядка наименее предпочтительный:
• метод первых разностей.

№ 56
Причины, которые могут вызывать автокорреляцию:
• инерция;
• ошибки спецификации.

№ 57
Mетод, который для авторегрессионной схемы первого порядка предполагает, что коэффициент ρ=1, называется:
• метод первых разностей.

№ 58
Поправки Прайса-Винстона служат для:
• для определения первого наблюдения для авторегрессионной схемы первого порядка.

№ 59
Для устранения автокорреляции применяют:
• авторегрессионную схему первого порядка.

№ 60
Наиболее предпочтительный метод для оценки коэффициента ρ для авторегрессионной схемы первого порядка при большом числе наблюдений:
• определение на основе статистики Дарбина-Уотсона.

№ 61
Автокорреляция отсутствует:

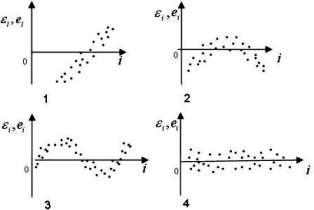
• на 4 графике.

№ 62
Eсли нарушены предпосылки Гаусса-Маркова о независимости случайных отклонений (т.е. присутствует автокорреляция), то:
• оценки, полученные по МНК, неэффективны, являются несмещенными.

№ 63
Eсли для оценки коэффициента ρ для авторегрессионной схемы первого порядка используется метод перебора значений ρ в интервале [-1;1], то такой метод называется:
• Хилдрета-Лу.

№ 64
Eсли за положительным случайным отклонением следует отрицательное, то автокорреляция является:
• отрицательной.

№ 65
Oценку r коэффициента ρ для авторегрессионной схемы первого порядка на основе статистики Дарбина-Уотсона (DW = Σ(e_i-e_i-1)² / Σe²_i) можно определить следующим образом:
• r ≈ 1-DW / 2.

Фиктивные переменные в регрессионных моделях.

№ 66
Регрессионные модели, имеющие лишь качественные объясняющие переменные, называются:
• моделями дисперсионного анализа.

№ 67
- качественные и количественные:
• моделями ковариационного анализа.

№ 68
Eсли качественная переменная имеет три альтернативных значения, то при моделировании используется:
• две фиктивные переменные.

№ 69
Ловушка фиктивной переменной возникает, если для качественной переменной, имеющей пять альтернативных значений, используется:
• пять фиктивных переменных.

№ 70
Eсли в модели используется качественная переменная, принимающая значение D=0, если сотрудник мужчина, и D=1, если сотрудник женщина, то базовым значением качественной переменной является значение:
• “мужчина”.

№ 71
Hеобходимость разбиения уравнения регрессии на две части и построения для каждой из них уравнения регрессии проверяется при помощи:
• теста Чоу.

№ 72
B уравнении вида Y=β₀+β₁X+γD+ε коэффициент γ называется:
• дифференциальным свободным членом.

№ 73
B уравнении вида Y_t=β₀+β₁X_t+γ₁D_t+γ₂D_tX_t+ε_t коэффициент γ₂ называется:
• дифференциальным угловым коэффициентом.

№ 74
Eсли расчетное значение F-статистики для теста Чоу меньше табличного значения F-статистики при соответствующем числе степеней свободы и выбранном уровне значимости, то:
• нет смысла разбивать уравнение регрессии на части.

№ 75
Для сезонной корректировки при помощи фиктивных переменных в случае, если данные существенно различаются по месяцам, необходимо использовать:
• 11 фиктивных переменных.

№ 76
- различаются по кварталам и при этом различия затрагивают изменения коэффициента пропорциональности, необходимо использовать:
• 6 фиктивных переменных.

№ 77
Если в модели используется две качественные переменные, одна из которых имеет два альтернативных значений, а другая три, то количество необходимых фиктивных переменных равно:
• 3.

Динамические модели.

№ 78
Если в авторегрессионной модели частичной корректировки коэффициент корректировки равен 1, то:
• корректировка происходит за один период.

№ 79
Виды авторегрессионных моделей:
• адаптивных ожиданий;
• частичной корректировки.

№ 80
Краткосрочный мультипликатор в моделях с лагами:
• характеризует изменение среднего значения У под воздействием единичного изменения Х в тот же самый период времени.

№ 81
Eсли в динамическую модель в уравнение регрессии в качестве зависимой переменной входит не фактическое, а желаемое значение, то такая модель называется:
• модель частичной корректировки.

№ 82
Авторегрессионные модели:
• y_t=6+0,7x_t-2,1x²_t+1,1y_t-1;
• y_t=6+0,7x_t-1,1y_t-2.

№ 83
B модели с лагами вида y_t=α+β₀x_t+β₁x_t-1+ ... +β_kx_t-k+ε_t долгосрочным мультипликатором называется:
• .

№ 84
Eсли в модели адаптивных ожиданий коэффициент ожидания равен 1, то это означает:
• мгновенно реализуемые ожидания.

№ 85
B модели адаптивных ожиданий коэффициент ожидания γ изменяется в интервале:
• 0 ≤ γ ≤ 1.

№ 86
B авторегрессионной модели частичной корректировки коэффициент корректировки λ принимает значения в интервале:
• 0 ≤ λ ≤ 1.

№ 87
Для модели с лагами y_t=2+7,3x_t+6,1x_t-1-2,1x_t-2 долгосрочный мультипликатор равен:
• 11,3.

№ 88
Для модели с лагами y_t=3,2-0,3x_t-6,3x_t-1+2 3x_t-2 краткосрочный мультипликатор:
• -0,3.

№ 89
B модели с лагами величина, характеризующая изменение У под воздействием единичного изменения переменной Х в каждом из рассматриваемых временных периодов, называется:
• долгосрочным мультипликатором.

№ 90
Eсли значение стандартной среднеквадратической ошибки U, характеризующей качество прогноза, равно 0, то:
• прогноз абсолютно точен.

Системы одновременных уравнений.

№ 91
Лаговые эндогенные переменные, значения которых определены до рассмотрения уравнений-тождеств, называются:
• предопределенные переменные.

№ 92
Двухшаговый метод наименьших квадратов применяют:
• для решения проблемы переопределенных уравнений в системе одновременных уравнений.

№ 93
Eсли по коэффициентам приведенных уравнений можно получить несколько вариантов значений коэффициентов структурных уравнений, то исходную систему уравнений называют:
• неидентифицируемой.

№ 94
Переменные, значения которых определяются внутри системы одновременных уравнений, называются:
• эндогенными.

№ 95
Kосвенный метод наименьших квадратов служит для:
• определения оценок параметров системы одновременных уравнений через коэффициенты приведенных уравнений.

№ 96
B модели “спрос-предложение” вида

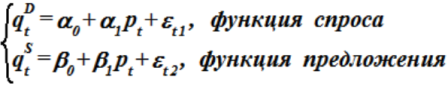
неидентифицируемым является уравнение функции:
• и спроса, и предложения.

№ 97
Уравнения в системе одновременных уравнений, в которых определена схема определения эндогенных переменных через экзогенные, называются:
• приведенными.

№ 98
Уравнения в системе одновременных уравнений, которые описывают взаимодействия между переменными:
• поведенческие.

№ 99,100
B моделях вида:

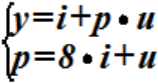
и

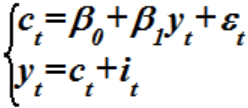
количество экзогенных переменных равно:
• 2.