Электродинамика и техника СВЧ
для специальности 200307
Соколова Ж.М., Шангина Л.И.
Кафедра РЗИ
Томск-2001

№ 1
Через замкнутое кольцо с радиусом a протекает два потока
,
отличающиеся только наклоном к нормали - круга 90° и 120°.
ЭДС, возбуждаемая в кольце этими потоками:
• Э=0,5ωπa²B₀costω.

№ 2
Если в анизотропной среде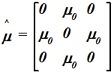
и , то вектор направлен:
• .

№ 3

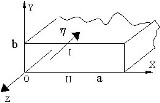
Граничные условия для магнитного поля при наличии поверхностных токов на стенках металлической трубы, представленной на рисунке. Cчитать I-ой средой объем внутри трубы.
• при y = 0, y = b.

№ 4
Условия, при котором выполняется равенство
, где - радиус-вектор, - вектор напряженности магнитного поля:
• =0.

№ 5
Вектор D и его направление в среде с проводимостью, равной нулю, если
, где k=const, ω=const.
• .

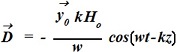№ 6
Удельная проводимость среды выражается тензором. Если =₀+₁, где
(k - постоянная), этот имеет вид:
• .

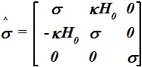№ 7
Если нормаль к площадке и вектор =B₀sinωt, в поле которого оказались площадки, расположены под углом ϑ, наибольшая ЭДС возникает в замкнутом контуре:
• .

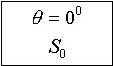№ 8
Векторы , , если
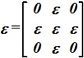, а =₀E, расположены под углом:
• 90°.

№ 9
Вдоль тонкостенной трубы радиуса a и тонкого проводника, совпадающего с осью трубы протекают постоянные токи I₂ и -I₁. (μ=μ₀). Магнитное поле в точках, отстоящих от оси трубы на расстояниях a/2 и 3a:

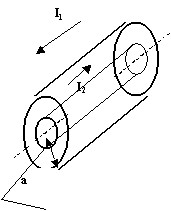
• H₁ = I₂ / (πa), H₂ = (2I₂-3I₁) / (12πa).

№ 10
Если при тех же и , ε и σ среды увеличатся вдвое, то токи проводимости (_np) и смешения (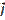_см):
• удвоятся.

№ 11
По идеально проводящей плоскости протекает постоянный ток, причем поверхностная плотность тока A/м в каждой точке вблизи плоскости.

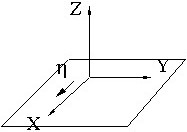
Магнитное поле в любой точке вблизи плоскости:
• =-η A/м.

№ 12
Металлический шарик радиусом r = 1 см заряжен положительным зарядом q=4*10^-9 Кл. Справка: Диэлектрическая проницаемость среды ε=2,5*10^-8 ф/м. Напряженность электрического поля на расстоянии 2 м от центра заряженного шарика:
• =0,03 B/м.

№ 13
Представленные поля, изменяющиеся во времени и в пространстве при μ=const, могут быть полями вектора, удовлетворяющими уравнениям Максвелла (т.е. могут быть реализованы):
• ₁ = 9x cost ω - 9y cost ω;
• ₂ = cosx sint ω + siny cost ω;
• ₃ = 6xy cost ω - 3y² cost ω.

№ 14
Если вектор направлен параллельно оси oy, то линии полного тока расположены:
• в плоскости xoz.

№ 15
Вблизи металлической поверхности задано распределение вектора D = 5 + 5 √(3) . Полагая, что поле в металле отсутствует, определить поверхностную плотность заряда на поверхности металла.

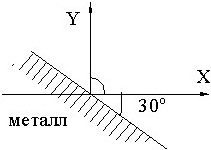
• ζ=10.

№ 16
Диэлектрик коаксиального кабеля имеет удельную проводимость σ. Напряженность электрического поля E внутри кабеля, если ток утечки на единицу длины равен I:
• =₀I / (2πσr).

№ 17
Вектор D направлен под углом 45° к границе раздела двух сред, диэлектрические проницаемости которых равны ε₁=1, ε₂=√3. Поверхностная плотность заряда ζ=0. Угол α₂ между и границей раздела:
• α₂=30°.

№ 18
Величина и направление вектора силы , воздействующей на заряд q=10^-5 Кл, движущейся в плоскости YOX со скоростью ν=10⁴ м/c под углом α=45° к однородному полю вектора ||=10^-2 кг/(A*сек²):

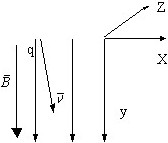
• =0,707*10^-3.

№ 19
В диэлектрике с конечной проводимостью σ≠0 переменное электрическое поле, не порождающее магнитного поля:
• затухающее во времени экспоненциально.

№ 20
Поток вектора плотности полного тока _полн через поверхность куба со стороной a:

• П=j_полн=0.

№ 21
Если вектор направлен всюду параллельно оси OX, то линии полного тока расположены:
• в плоскости YOZ.

№ 22
Если при тех же и параметры среды ε и σ учетверить, токи проводимости j_пр и смещения j_см:
• j_см=4j_смо; j_пр=5δj_про.

№ 23
В любой точке объёма V, где существуют только токи проводимости и токи смещения = -gradφ(x, y, z, t). Вектор в наиболее общем случае:
• экспоненциально убывает во времени.

№ 24
Внутри полой металлической трубы радиуса a (цилиндрическая система координат - r, a, z) возбуждено переменное электрическое поле. Граничные условия для магнитного поля на стенках (r = a), считая поле в металле равным нулю (η - плотность поверхностного тока):
• B_r=0, H_α=-η_z, H_z=η_α.

№ 25
Шар радиусом 2а равномерно заряжен. Плотность объёмного заряда ρ. Вектор на расстоянии а и 2а от центра шара:
• D_a=aρ/3, D_2a=2aρ/3.

№ 26
В некотором объеме свободного пространства имеется электрическое поле =10 B/м и магнитное поле =15 A/м. Заряд q=10^-9 Кл впрыскивается в этот объем со скоростью =21*10⁶ м/c. μ₀=4π*10^-7 Гн/м. Сила, действующая на заряд и ее напряжение:
• 28,84*10^-9.

№ 27
Металлический шар радиусом а помещен в поле Е₀ заданное уравнением φ(r)=E₀(a³/r²-r)cosϑ. Поверхностная плотность заряда ζ на шаре, если ∂φ/∂n = E_n:
• ζ=3εE₀cosϑ.

№ 28
Вектор электромагнитного поля равен = E₀sin(ωt - ω √(εμ) z).
• Вектор = √(ε/μ) E₀sin(ωt - ω √(εμ) z).

№ 29
По двум параллельным проводам, отстоящим один от другого на расстоянии L протекают постоянные однонаправленные токи I₁ и I₂. На линии их соединяющей, расположена точка, на которой магнитное поле равно нулю. Расстояние точки от первого провода:
• r=LI₁/(I₂+I₁).

№ 30
Если =E в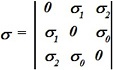
, то вектор плотности тока проводимости:
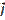• _пр=σ₁E+σ₂E.

№ 31
Между электродами конденсатора поддерживается постоянная во времени разность потенциалов равная 500 В. В электродах проделано сквозное очень маленькое отверстие, через которое пролетает электрон, вращающийся по окружности. (1 эВ - энергия, приобретенная электроном при прохождении разности потенциала в 1 В).

Энергия электрона изменится на 5 КэВ через:
• 10 оборотов.

№ 32
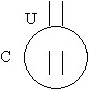
Величина напряжённости магнитного поля в середине между двумя параллельными, бесконечными проводниками, по которым текут одинаковые, но противоположные по направлению постоянные токи:

• H=J/(πa).

№ 33
В объёме V имеется два точечных заряда Q₁=2 Кл и Q₂. Если известно, что поток вектора через поверхность S, охватывающую объём V, равен 1 Кл, величина заряда:
• Q₂=-1 Кл.

№ 34
Напряжённость электрического поля изменяется по закону E_х=E₀a/x; E_y=0; E_z=0. Плотность объёмного заряда:
• ρ=-ε₀E₀a/x².

№ 35
Магнитное поле =[×], где - радиус-вектор точки, создается токами:
• протекающими параллельно оси z с плотностью, независящей от координат.

№ 36
Электронный поток в электронно-лучевой трубке имеет радиус а = 1 мм, объёмную плотность ρ=3*10^-8 Кл/м³ и движется со скоростью V=5*10⁷ м/с. Ток в трубке:
• 4,71 мкА.

№ 37
Вблизи границы раздела двух сред (x = 0) задано распределение вектора . ₁=(5+5) x>0; ₂=(4+3) x<0.
• 3 из приведенных утверждений верны:
1. На границе раздела есть поверхностный заряд;
2. В средах 1 и 2 отсутствуют объемные заряды;
3. Одна из сред обязательно анизотропна;
4. Густота силовых линий вектора в обеих средах одинакова.

№ 38
В идеальном диэлектрике (σ=0) в отсутствие токов переноса и сторонних токов вектор =H_x(x, y, z):
• Вектор =E_y+E_z.

№ 39
Сердечник трансформатора выполнен из стали с плотностью 7,7 г/см³ и имеет массу 2 кг. Амплитудное значение магнитной индукции 2,1 Тл, относительная магнитная проницаемость стали μ=200. Максимальное значение энергии, запасаемой в сердечнике, при намагничивании его синусоидальным током:
• 2,279 Дж.

№ 40
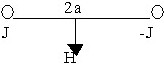
Для неоднородного диэлектрика с параметром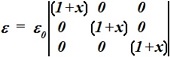
:
• вектор =(E_x+E_y)(1+x)ε₀.

№ 41
В однородной и изотропной среде с параметрами ε, μ, σ векторы и в объеме U оказались паралельными и пропорциональными друг другу в каждой точке объема. = √(ε/μ). Токи переноса и сторонние токи равны нулю. В наиболее общем случае поле при этом должно быть:
• =₀(x, y, z)e^-(σ/2ε)t.

№ 42
На углах равностороннего треугольника расположены три одинаковых заряда q = 1 Кл.

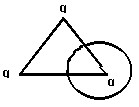
Поток вектора через сферу, радиус которой равен половине стороны треугольника, а центр совпадает с одним из зарядов, равен:
• 1 Кл.

№ 43
Напряженность поля в любой точке пространства, созданного объёмным зарядом, распределенным с постоянной плотностью ρ внутри шара с радиусом a (Всюду ε=ε₀):
• E_R≤a=ρR/(3ε₀); E_R>a=ρa³/(3ε₀R²).

№ 44
Ток возникает в среде за счет движения объёмного заряда со скоростью =5x. (Считать плотность тока - const; другие типы токов отсутствуют). Зависимость объёмной плотности заряда от координат:
• ρ=c/x.

№ 45
Через замкнутый проводник, ограничивающий круг с радиусом а, протекает два потока вектора =B₀sinωt, отличающиеся только углом по отношению к нормали круга 60° и 120°.

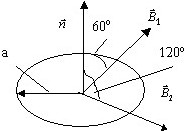
ЭДС, возбуждаемая в кольце этими потоками:
• 0.

№ 46
Поле бесконечно длинной однородно-заряженной нити (теорема Гаусса):
• =τ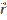₀/(2πε₀r), τ - заряд на единицу длины.

№ 47
В однородной и изотропной среде задано поле Е_х. Все токи, кроме тока смещения, отсутствуют.
• H_x=0, D_y=D_z=0.

№ 48
Имеются 2 полубесконечных cреды: изотропная (1-ая) и анизотропная (2-ая). В 1-ой среде плотность тока проводимости ₁= и проводимость σ₁=σ, во второй среде проводимость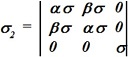
.

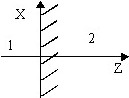
Вектор во 2-ой среде:
• ₂=₁(α+β).

№ 49
Однородное поле вектора =B₀sinωt пересекает площадки ограниченные замкнутыми проводниками, расположенными под углами к этому вектору. (∂B/∂t)ds=ЭДС. Электродвижущая сила (ЭДС) равна нулю:
•

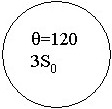
№ 50
Три параллельных проводника с одинаковыми токами проходят через вершины равностороннего треугольника, плоскость которого перпендикулярна проводам. Сторона треугольника равна а.

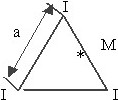
Магнитное поле в середине одной из сторон:
• I/(πa√3).

№ 51
В любой точке пространства, где существует только токи проводимости и токи смещения, =grad ψ(, t), где ψ - произвольная функция и t. Вектор :
• Е - экспоненциально убывает во времени.

№ 52
Е - вектор напряженности электрического поля, независимый от времени, а r - радиус-вектор точки. div [, ] равно:
• 0.

№ 53
Система уравнений электромагнитного поля, не зависящего от времени в проводящей среде без сторонних токов и зарядов:
• rot =_np; rot =0; div =0; div =0.

№ 54
На границе двух сред векторы ₁ и ₁₁ будут ₁=2+5+4, ₁₁=4+5+8.

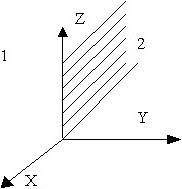
• обе среды обязательно анизотропны.

№ 55
Замкнутое проводящее кольцо с радиусом а, пронизывает два потока вектора =B₀cosω*t, отличающиеся только наклоном к нормали круга 30° и 150°. ЭДС, возбуждаемая в кольце этими потоками:

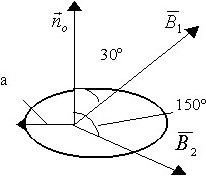
• 0.

№ 56
Физическое толкование уравнения rot =10 :
• проекция вихря вектора на ось z и она равна плотности тока 10 А/м².

№ 57
Плотность поверхностного заряда (Кл/м²) на границе раздела сред, при условиях ε₁=ε₀, ε₂=4ε₀, Е_п2=2Е_п1=36π в/м, ε₀=(π/36)*10^-9 ф/м:
• 3,5*10^-9 Кл/м².

№ 58
Пучок электронов, излучаемый катодом, имеет вид цилиндра с радиусом а и обладает скоростью v₀ и плотностью объёмного заряда ρ₀. Напряженность магнитного поля внутри и вне пучка:
• H_внутр=ρ₀v₀r/2, H_вне=ρ₀v₀a²/(2r).

№ 59
В идеальном диэлектрике (σ=0) задано распределение вектора = siny cost. Вектор этого поля:
• =-(1/ε) cosy sint.

№ 60
В случае

• поток вектора электрической индукции не имеет направления.

№ 61
Поток вектора =a₀/r, где r²=x²+y²+z² через поверхность сферы при r=2 м с центром в точке r=0:
• 8π*a.

№ 62
В кубе с ребром равным а, если начало координат расположено на вершине куба, а ось совпадает с одним его ребром, а вектор =(x²/2).

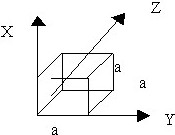
заряд равен:
• a⁴/2.

№ 63
Внутри полой металлической трубы радиуса А (круглый волновод) возбуждено переменное электромагнитное поле. Граничные условия для магнитного поля на стенках (r=A), считая поле в металле равным нулю:
• H_r=0, H_α=-η_z, H_z=η_α, η - плотность поверхностного тока.

№ 64
Шар с радиусом 2а равномерно заряжен, плотность объёмного заряда ρ. Вектор на расстоянии а и 2а от центра шара равен:
• _a=aρ/3; _2a=2aρ/3.

№ 65
Цилиндр радиусом r=R и высотой h. Ось цилиндра совпадает с осью координат OZ. Поле равно =-, где =⁰√(x²+y²) и ₀ - единичный вектор в плоскости XOY вдоль координаты . Поток вектора через поверхность цилиндра:
• -10π*h*R.

№ 66
Вектор =y²-x. Объёмный заряд, создающий это поле:
• 0.

№ 67
Вектор =_x, среда изотропная:
• вектор =_y+_z.

№ 68
В любой точке пространства =-gradψ(r, t), где ψ - функция времени и координат.
• вектор =0, не зависит от времени.

№ 69
По поверхности идеального проводника, совпадающей с плоскостью XOY, протекает поверхностный ток А/м, направленный против оси Х. Z>0.

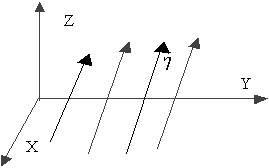
Магнитное поле в любой точке над поверхностью проводника:
• =η A/м.

№ 70
Некоторый анизотропный диэлектрик имеет тензор относительной диэлектрической проницаемости, который в декартовой системе координат записывается таким образом:
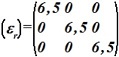. В диэлектрике создано равномерное электрическое поле Е=2,5 E=2,5+1,7+9,2. Вектор электрической индукции и угол в пространстве между векторами и :
• =ε₀(16,25+11,05+61,18), ∠ (*)=6,59*10^-3 рад.

№ 71
Вектор направлен под углом 30° к границе раздела двух сред, диэлектрические проницаемости которых равны ε₁=1, ε₂=√3. Угол α₂ между ₂ и границей раздела:
• 45°.

№ 72
Физический смысл третьего уравнения Максвелла

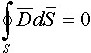
• внутри замкнутой поверхности S нет ни источников, ни стоков поля, поток вектора D через S равен нулю.

№ 73
В некоторой точке пространства вектор напряженности электрического поля =20 B/м в то время как вектор Пойнтинга =10+30 A/м². Вектор напряженности магнитного поля:
• -1,5+0,5 A/м.

№ 74
Поток вектора плотности полного тока _пол=5x₀+7y₀+8z₀ через поверхность куба со стороной а=5 m:
• 0.

№ 75
В среде с параметрами ε, μ и σ=0 возможны токи:
• _cm+_nep+_cm.

№ 76
Имеются две полубесконечные среды, 1-ая - изотропная с μ₁=μ, 2-ая - анизотропная с
.
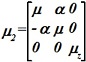Токов в средах нет. Вектор магнитного поля ₂ во второй среде, если поле ₁ в первой среде задано ₁=_y1:

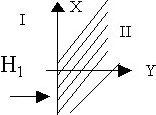
магнитное поле во 2-ой среде, если в первой ₁=_y1.
• _2y=_y1, _2x=0, _z2=0.

№ 77
Поток вектора _пол=5+7+8 через сферу радиусом а=1 см:
• 0.

№ 78
Внутри металлического полого шара с радиусом а распределен заряд с объёмной плотностью ρ=10^-6 Кл/м³. Поверхностная плотность заряда на шаре (внутри поверхности):
• ζ=-ρa/3.

№ 79
Вектор =E₀cost sinx.
• вектор =E₀ cosx sint.

№ 80
Выражение вектора для неоднородного диэлектрика с параметром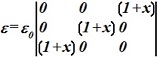
если задано поле =E_x+E_y:
• =(E_x+E_y)(1+x)ε₀.

№ 81
Вектор =z³-x²-y. Объёмный заряд, создающий это поле:
• 0.

№ 82
Символическое определение первого уравнения Максвелла:
• .

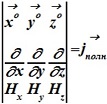№ 83
Магнитного поля с распределением вектора магнитной индукции =5x²+5y²+5z²:
• нет.

№ 84
По двум параллельным, прямолинейным проводникам протекают одинаковые по величине, но противоположные по направлению постоянные токи.

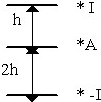
Напряженность магнитного поля в точке A:
• I/(4hπ).

№ 85
Полный ток, вытекающий из шара радиусом а, если плотность тока равна =x_м+y-2z:
• 1/(3πa³).

№ 86
В однородной и изотропной среде с параметрами ε, μ σ векторы и оказались в каждой точке в объёме пропорциональными и параллельными друг другу. 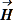= 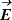√(ε/μ). Поле Е:
• должно быть E=₀(x, y, z)e^-(σ/2ε)t.

№ 87
В верхнем полупространстве x>0 вектор =5x. При х<0 задано, что =0. Это поле создают:
• объёмные заряды с ρ=5.

№ 88
Среда с пространственной дисперсией:
• .

№ 89
В замкнутом контуре, изображенном на рисунке в виде треугольника АВС, если известен вектор =₀sin wt:

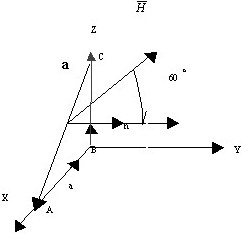
• ЭДС=(ωμa²/4)₀cos wt.

№ 90
Вектор электрического смещения равен =x+y-(x+y). Объемная плотность заряда:
• 2 Кл/м³.

№ 91
В вакууме существует электромагнитное поле гармонически изменяющееся во времени. В некоторой точке пространства вектор =130 cos2π*10¹⁰*t. Плотность тока смещения в данной точке:
• -0,455sin2π*10¹⁰*t*.

№ 92
В некоторый момент тело, характеризуемое диэлектрической проницаемостью ε=3ε₀ и удельной проводимостью σ=9,78*10^-10 См/м несет электрический заряд. Промежуток времени, в течение которого заряд любой внутренней области уменьшится вдвое:
• 0,0169 cекунд.

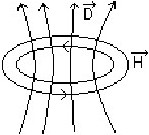
№ 93
:
•

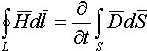№ 94
В диэлектрике с конечной проводимостью σ ≠ 0 переменное электрическое поле, не порождающее магнитного поля:
• падает во времени экспоненциально.

№ 95
Квадратная рамка со стороной а помещена в магнитное поле 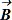=B₀sinωt так, что вектор магнитной индукции составляет угол 60° с нормалью к плоскости рамки.

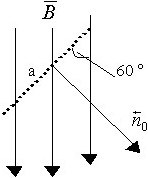
Ток, протекающий в рамке, если сопротивление её R, равен
• J=ωa²B₀cosωt/2R.

№ 96
Грозовая туча, имеющая площадь 5 км², располагается на высоте 2 км от поверхности Земли. Между тучей и Землей образуется постоянное электрическое поле с одинаковой во всех точках напряженностью Е=2*10⁴ В/м. Энергия поля:
• 1,77*10⁹ Дж.

№ 97
Напряженность поля в любой точке пространства, созданную объёмным зарядом, распределенным с постоянной плотностью ρ внутри шара с радиусом а, (ε=e₀):
• E_R≤a=ρa/(3ε₀); E_R>a=ρ*a³/(3ε₀R²).

№ 98
В однородной и изотропной среде задано распределение вектора =E₀(y-x)cos wt.
• вектор = 2E₀sint / wμ.

№ 99
Закон Ома в дифференциальном виде:
• =σ.

№ 100
Величина и направление вектора силы , воздействующей на заряд q=10^-5 Кл, движущейся со скоростью ν=10⁵ м/c в плоскости рисунка под углом α=30° к однородному полю вектора ||=10^-3 кг/(a*сек²).

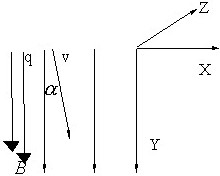
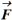• =0,5*10^-3H.