Электродинамика и распространение радиоволн
Соколова Ж.М., Мандель А.Е.
Кафедра РЗИ
Томск-2000

№ 1
Если диэлектрическая проницаемость среды представлена тензором
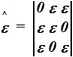, а вектор =E₀, векторы и расположены под углом:
• 60°.

№ 2
Вектор ₁ направлен под углом 60 градусов к границе раздела двух сред, диэлектрические проницаемости которых относятся как ε₁/ε₂=1/√(3). Поверхностный заряд отсутствует. Угол α₂ между ₂ и границей раздела:
• 45°.

№ 3
Поток вектора плотности полного тока _пол=(δ₀/r)₀ (δ₀ - постоянная величина) через поверхность цилиндра, высота которого h, радиус - a:
• δ₀2πh.

№ 4
В однородной и изотропной среде задано распределение вектора =E₀cos(wt-kz). Определите вектор .
• .

№ 5
Плотность тока в среде =(σ₁E_x+σ₂E_z)+σ₀E_y+(-σ₁E_x+σ₂E_z), тензор удельной проводимости:
• .

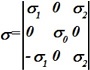№ 6
Вектор напряженности электрического поля в декартовой системе координат имеет единственную составляющую E_y отличную от нуля. Вектор Пойнтинга будет иметь составляющие:
• П_x,П_z.

№ 7
Мгновенные значения векторов поля в фиксированный момент времени известны и равны =₀cos(wt+θ₁), =₀cos(wt+θ₂). Мгновенное значение вектора Пойнтинга:
• 1/2[₀*₀]cos(θ₁-θ₂)+1/2[₀*₀]cos(2wt+θ₁+θ₂).

№ 8
Величина и направление силы F, воздействующей на заряд q=10^-5 Кл движущийся со скоростью =10⁶ м/c в магнитном поле вектора =10^-2(-):
• =0,1+).

№ 9
Выражение вектора для неоднородного диэлектрика с параметром
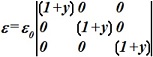если задано электрическое поле вида =E_x-E_y. Значение E_x и E_y.
• =ε₀(1+y)(E_x-E_y); E_x=C₁; E_y=C₂/(1+y).

№ 10
В однородной и изотропной среде известен вектор =H₀sin(wt-kx).
• Вектор .

№ 11
Пучок электронов имеет вид длинного цилиндра с радиусом а, обладает скоростью V₀ и плотностью объемного заряда ρ₀=const. Напряженность магнитного поля на расстоянии b, причем b>a:
• _b=(ρ₀V₀a²₀)/(2b).

№ 12
Граница раздела двух однородных и изотропных сред, имеющих электродинамические параметры ε₁ и ε₂, имеет уравнение x=0. В первой среде известен вектор напряженности ₁=E₀cosξx+E₀cosηy. Поверхностные заряды отсутствуют. Вектор ₂ вблизи границы:
• ₂=E₀ε₁/ε₂+E₀cosηy.

№ 13
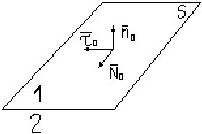
Граничные условия в векторной форме для тангенциальных составляющих векторов поля и , учитывая, что вектор нормали к плоскости S образует с ₀ и ₀ правую тройку ₀=[₀*].

• [ × (₁-₂)]=0; [ × (₁-₂)]=_поверх.

№ 14
Поток вектора
через поверхность куба, сторона которого а (среда однородна и изотропная):
• -10a².

№ 15
Поверхностная плотность заряда на границе y=0, если известны параметры ε₁=ε₀, ε₂=3ε₀ и векторы напряженности электрического поля в средах ₁=3cosξy cos(kz+wt), ₂=cosξy cos(kz+wt):
• 0.

№ 16
В морской воде и сухой почве при распространении волны с частотой f=10⁵ Гц, если электрофизические параметры как на графике (справка: J_пол.=J_смещ.+J_{провод.})

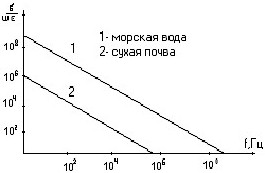
могут существовать токи
• J_{полн.вода}=J_{провод.}; J_{полн.почва}=J_провод+J_смещ..

№ 17
Для системы двух полубесконечных металлических электродов получено общее решение уравнения Лапласа в виде θ=(A₀Ln r+B₀)*(C₀α+D₀)+∑_λ((A_λr^λ+B_λr^-λ)*(C_λsinλα+D_λcosλα)). Определите константы и получите решение для θ.

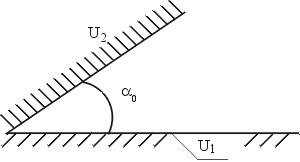
• θ=(U₂-U₁)α/α₀+U₁.

№ 18
В неоднородной среде с диэлектрической проницаемостью ε=ε₀y электростатическое поле зависит только от координаты y в области a<y<b. Объемные заряды отсутствуют. Выражения для напряженности и потенциала:
• =(C₁/(ε₀y)); θ=-C₁/ε₀ ln y+C₂.

№ 19
Плотность тока во второй среде, если напряженность электрического поля в первой среде имеет вид ₁=(+)E₀, где E₀=const, а удельной проводимости сред заданы.

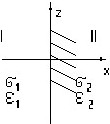
• ₂=(σ₁+σ₂)E₀.

№ 20
Из точки А(3,6,0) в точку В(9,-7,3) перемещается заряд q в поле =E₁+E₂-E₃. Работа, совершаемая полем:
• A=q(6E₁-13E₂-3E₃).

№ 21
Потенциал поля, если вектор напряженности электростатического поля равен = Asin kx + Bsin ky, (A,B - const):
• θ = (A/k)cos kx + (B/k)cos ky.

№ 22
Векторное поле задано выражением =(E₀/r³)(₀2cosϑ+sinϑ). Уравнение векторных линий:
• r=(c*sinϑ)².

№ 23
Система длинных заряженных нитей (l>>r_i).

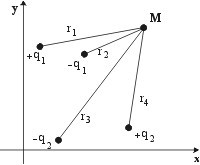
Поперечные размеры нитей малы. Среда - воздух. Потенциал в точке M(x,y):
• θ_M = (q₁/2πεl) ln(r₂/r₁) + (q₂/2πεl) ln(r₃/r₄).

№ 24
Куб со стороной а. Начало координат расположено в вершине. Диэлектрическая проницаемость среды ε. Потенциал электростатического поля внутри задается выражением θ=x²-z². Энергия электростатического поля, запасенная в объеме куба:
• 4/3 εa⁵ дж.

№ 25
Пространство между двумя металлическими пластинами, находящимися на расстоянии d друг от друга (d много меньше линейных размеров пластины), заполнено диэлектриком с проницаемостью ε_a=3ε₀ d/y. Одна пластина заземлена (при y=0), а на другой потенциал U. Потенциал и поверхностная плотность заряда на электроде y=d:
• θ=Uy²/d²;
• ξ=6Uε₀/d.

№ 26
Шар радиусом b, помещен на высоте h над проводящей плоскостью. Диэлектрическая проницаемость среды ε_a=3ε₀ Ф/м. Принять b<<h. Собственная емкость шара:
• C=24πε₀bh/(2h-b).

№ 27
Внутренняя индуктивность цилиндрического проводника μ=μ₀ длиной 2 см и радиусом 2 мм на низких частотах:
• L=10^-7 Гн.

№ 28
Для провода длиной l, радиусом a и μ=μ₀, собственная энергия магнитного поля при протекании тока J:
• W = μ₀J²l / 16π Дж.

№ 29
Соотношение для определения в объеме V энергии магнитного поля, созданного системой линейных токов, если известен векторный потенциал в этом поле:
• .

№ 30
Соотношение для определения энергии электростатического поля в объеме V, если известно выражение для потенциала, созданного зарядами:
• .

№ 31
На кольцевом сердечнике из ферромагнитного материала (μ>>1) намотано 3 витка (N=3). Рассеянием поля H пренебречь.

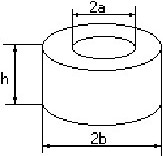
Индуктивность этой катушки:
• L_N=(μhN²/2π) ln(b/a).

№ 32
Решение уравнения ∇²(z)=μz для векторного потенциала в магнитном поле токов:
• (z)=μz³/6+C₁z+C₂).

№ 33
Два концентрических витка с радиусами R₂ и R₁, причем R₂>>R₁, находящимися друг относительно друга по оси z на расстоянии l. Считать, что магнитное поле на оси витка определяется соотношением
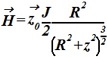, где z - осевая координата. Взаимная индуктивность:
• .

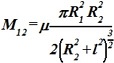№ 34
Работа, которую необходимо затратить на перемещение заряда q Кл из точки М(3,5,0) в точку N(-7,9,2) в электрическом поле =(2+5+10) В/м:
• A=20q, КлВ.

№ 35
Длина волны, распространяющейся в воздухе, составляет 1м. Длина волны при той же частоте в меди и свинце (σ_Си=5,65*10⁷ 1/ом*м; σ_Pb=0,48*10⁷ 1/ом*м; μ=μ₀; ε=ε₀):
• 0,024 мм; 0,083 мм.

№ 36
Амплитуда напряженности магнитного поля плоской электромагнитной волны, распространяющейся в среде с параметрами μ_r=1, σ=2*10^-4 см/м ε_a=4ε₀, в плоскости z=0 равна 1 А/м. Частота сигнала 10⁷ ГГц. Среднее значение плотности потока энергии волны на расстоянии z=1 м от начала координат:
• 87,9 Bm/м².

№ 37
Коэффициент затухания электромагнитной волны с частотой f=10⁶ Гц, распространяющейся в морской воде, параметры которой σ_вода=0,45*10² 1/ом*м ε_{r вода}=81, μ=μ₀:
• 115,6 дБ/м.

№ 38
Выражение вектора и среднее значение вектора Пойнтинга для плоской электромагнитной волны, в свободном пространстве, заданной вектором =E₀e^jkz.
• =-(E₀/W₀)e^jkz; =-(E₀²/2W₀).

№ 39
Удельная энергия электромагнитного поля, переносимого плоской волной, распространяющейся по оси y в среде ε_a=9ε₀, μ=μ₀, σ=0 на частоте f=10⁶ Гц, если амплитуда напряженности электрического поля E₀=10⁴ B/м.
• 3,98*10^-3 Дж/м³.

№ 40
В среде с параметрами ε_r=2,25, μ_r=1, σ=0 распространяется плоская электромагнитная волна с амплитудой напряженности электрического поля 100 в/м. Среднее значение энергии, переносимое волной в направлении распространения:
• 19,90 Bm/м².

№ 41
Среднее значение потока энергии плоской электромагнитной волны распространяющейся в среде ε_a, μ_a, tg δ_ε < 1 на частоте ω, в плоскости z=const:
• .

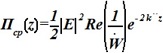№ 42
Плоская волна линейной поляризации распространяется в положительном направлении оси x в свободном пространстве. Ее вектор в виде суммы волн круговой поляризации:
• =(E₀/2)(+j)e^-jkx+(E₀/2)(-j)e^-jkx.

№ 43
Плоская электромагнитная волна распространяется в среде с параметрами ε_a=2ε₀, μ_a=μ₀, σ=3 1/ом*м вдоль координаты x. Мгновенные значения векторов поля и на частоте f=10⁷ Гц:
• =E_me^-10,9xcos(wt-10,9x); =(E_m/3,63)e^-10,9xcos(wt-10,9x-π/4).

№ 44
Средняя плотность потока энергии плоской волны круговой поляризации, распространяющейся в среде без потерь и имеющей вектор напряженности электрического поля вида _m=(E₀/2)(+j)e^-jkx:
• (E₀²/4W₀).

№ 45
Уравнение Гельмгольца для вектора электрического поля и для областей, содержащих источники с токами _cm и зарядами ρ̇_cm, для среды с параметрами ε_a, μ_a:
• .

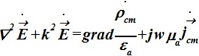№ 46
Волны, распространяются в морской воде с параметрами ε_a=81ε₀, μ_a=μ₀, σ=0,45*10² 1/ом*м. Частота сигнала 10⁶ Гц. Фазовая скорость, длина волны и коэффициент затухания:
• V_φ=4,7*10⁵ м/c; λ_в=0,47 м; α=13,31 1/м.

№ 47
Две плоских волны, электрические поля которых имеют вид ₁=2,1cos(wt-kz); ₂=1,2cos(wt-kz+π/2), пришли в точку z=const. Вид поляризации общего поля:
• эллиптическая поляризация с левым вращением.

№ 48
Выражения полей векторов и плоской волны, частота которой 10⁶ Гц, распространяющейся в сухой почве с параметрами ε_a=2ε₀, μ_a=μ₀, σ=10^-2 1/ом*м, вдоль координаты z:
• =Ae^-0,2(1+j)z; =(A/19,8)e^-0,2(1+j)ze^-jπ/4.

№ 49
Пучок оптического квантового генератора имеет площадь поперечного сечения 4 мм². Мощность генератора 1 Вт. Полагая, что в пределах пучка излучение генератора представляет собой плоскую электромагнитную волну, напряженность электрического поля:
• 13,73 B/мм.

№ 50
Плоская электромагнитная волна имеет частоту f=10⁷ Гц и распространяется в среде с параметрами ε_a=4ε₀, μ=μ₀, σ=2*10^-4 1/Ом*м. Амплитуда напряженности магнитного поля при z=0 равна 10 А/м. Плотность потока энергии волны на расстоянии z=1 м по отношению к началу координат изменится:
• на 4%.

№ 51
Особенности, соответствущие волнам, распространяющимся в проводящих средах:
• энергия полей сосредоточена в скин-слое;
• фазовая скорость увеличивается с ростом частоты.

№ 52
Диаграммы направленности магнитного диполя в дальней зоне.

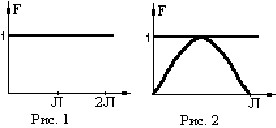
Они снимались:
• Рис.1: в плоскостях 0 ≤ θ ≤ 2π, ϑ=π/2;
• Рис.2: диаграмма снята при 0 ≤ ϑ ≤ π, α-const.

№ 53
К магнитному диполю заданных размеров подводится сторонний ток J_cm.m постоянной величины, но изменяющийся по частоте. Мощность излучения диполя от частоты в дальней зоне:
• P_изл=K*f⁴.

№ 54
Дифференциальные уравнения для электродинамических потенциалов и , которым они удовлетворяют в изотропных и однородных средах для гармонических во времени сторонних источников.
• .

№ 55
Отличие функции направленности по мощности от функции направленности по электрическому полю для магнитного диполя в дальней зоне:
• F_p(α,ϑ)=sin²ϑ; F_E(α,ϑ)=sin,ϑ.

№ 56
Теорема взаимности для случая, где (1) - передающая телевизионная антенна в объеме V₁, а в объеме V₂ - приемная антенна телевизора (2). Антенны находятся на расстоянии r >> λ.

• .

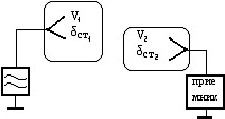
№ 57
Известно, что
(в сферической системе координат). Вектор :
• .

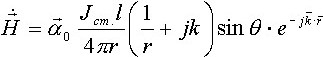№ 58
Виток с током (магнитный диполь), если его диаграмма направленности в экваториальной плоскости имеет вид окружности:

• расположен в экваториальной плоскости.

№ 59
Выражения векторов _m и _m магнитного диполя в дальней зоне по известным выражениям электрического диполя _ϑэ и _αэ:
• E ↔ H; ε ↔ -μ; ↔ ; p=-J_cml/w; m=J_cmμS.

№ 60
Соотношения для полей электрического диполя в дальней зоне по известным полям магнитного диполя: E_αm=((J_mk²SW₀)/(4πr))sinϑ*e^-jkr; H_ϑm=((J_mk²S)/(4πr))sinϑ*e^-jkr.
• H_αэ=-((J_эlk)/(4πr))sinϑ*e^-jkr; E_ϑэ=(kH_αэ)/(ωε).

№ 61
Мощность, излучаемую элементарным электрическим излучателем в сферический сектор, ограниченный углами ϑ₁=90°, ϑ₂=88°, при длине излучателя 5 см, амплитуда тока 10 А, длина волны 5 м:
• 10,36*10^-2 Bm.

№ 62
Мощность излучения элементарной рамки с током, если на расстоянии 500 м в экваториальной плоскости создается электрическое поле с амплитудой 100 мВ/м:
• 27,76 Вт.

№ 63
В электрической цепи существует ток с частотой 50 Гц и амплитудой 10 А. Площадь, ограниченная контуром цепи, составляет 4 м². Мощность, теряемая цепью за счет излучателя:
• 1,92*10^-20 Bm.

№ 64
Малая квадратная рамка в точке с координатами r =1000 м, ϑ=π/2. Амплитуда тока в рамке 1 А. Рамка лежит в экваториальной плоскости и имеет размер стороны 0,1λ₀. Амплитуды векторов напряженности электрического и магнитного полей:
• 11,838*10^-3 B/м; 0,0314*10^-3 А/м.

№ 65
Условие калибровки:
• div+jwμ_αε_α=0, оно вводится для упрощения уравнений для и .

№ 66
Отличие магнитных полей элементарного магнитного излучателя в ближней (H_бл) и дальней (H_д) зонах:
• _бл=H_rб0+H_ϑб0; _д=H_ϑд0;
• H_rб, H_ϑб ≈ 1/r³; H_ϑд ≈ 1/r.

№ 67
Определение полей и через динамические потенциалы и θ в случае электрического диполя:
• .

№ 68
Диаграмма направленности элементарного электрического диполя:

• снята в меридиональной при α-const.

№ 69
Отрезок провода длиной l можно считать элементарным электрическим излучателем на длине волны λ:
• если l << λ; J_cm=const.

№ 70
Функция направленности элементарного электрического диполя по мощности в экваториальной плоскости имеет вид:
• F=1.

№ 71
Условие, при котором волна любой поляризации, падающая на границу раздела двух сред под произвольным углом, во второй среде распространяется почти вдоль нормали к границе раздела:
• вторая среда - металл.

№ 72
Граничные условия Леонтовича применяются:
• когда |n₁/n₂| << 1; Δ⁰₂ << R₂ (R₂ - радиус кривизны, Δ - глубина скин-слоя).

№ 73
Нельзя пользоваться граничными условиями Леонтовича для волны частотой 0,1 МГц, падающей из воздуха на границу двух разных сред, имеющих параметры:
1) ε₁=ε₀, μ₁=100μ₀, σ₁=1 1/ом*м,
2) ε₂=10ε₀, μ₂=μ₀, σ=10^-2 1/ом*м,
при кривизне поверхности границы:
• R₁ ≥ 16 см R₂ ≥ 160 см.

№ 74
Соотношение волновых сопротивлений двух диэлектрических сред, если на границу раздела падает нормально плоская электромагнитная волна, и во второй среде среднее значение плотности потока мощности составляет 25% от этой величины в 1 среде:
• W₁/W₂=3.

№ 75
Плоская электромагнитная волна падает нормально на границу раздела воздух-диэлектрик с параметрами ε_r=4, μ_r=1, σ=0. Среднее значение плотности потока энергии в диэлектрике, если среднее значение плотности потока энергии падающей волны 4 Bm/м²:
• 32/9 Bm/м².

№ 76
На границу раздела двух сред падает волна под углом θ_n.

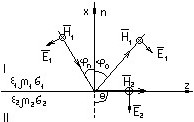
• поляризация волн - вертикальная;
• угол θ_n - критический, т.к. угол преломления ϑ=π/2.

№ 77
Горизонтально поляризованная волна падает под углом 30 градусов в первой среде. Параметры среды:
1) ε₁=ε₀, μ₁=μ₀, σ₁=0;
2) ε₂=100ε₀, μ₂=μ₀, σ₀=0.
Коэффициенты отражения и преломления:
• R_r=0,84, T_r=0,16.

№ 78

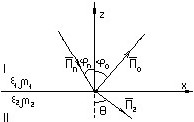
Считать θ_п=θ_пад, θ_о=θ_от. Законы Снеллиуса:
• θ_пад=θ_om; n,²sinϑ=n₁sinθ_пад.

№ 79
Когда волна горизонтальной поляризации падает под углом θ на границу раздела двух сред с параметрами ε₁, μ₁, ε₂, μ₂, то (в теории явлений на границе) должны зависеть от этих параметров и угла падения:
• коэффициенты отражения и преломления.

№ 80
Вертикально поляризованная волна падает под углом 30 градусов в первой среде. Параметры среды:
1) ε₁=ε₀, μ₁=μ₀, σ₁=0;
2) ε₂=100ε₀, μ₂=μ₀, σ₀=0.
Коэффициенты отражения и преломления:
• R_B=0,793, T_B=1,793.

№ 81
Вертикально поляризованная волна падает на границу раздела двух диэлектрических сред под углом α, лежащим в пределах 0<α<π/2. У отраженной волны электрофизическими величинами ε, μ должен определяться:
• коэффициент отражения.

№ 82
При падении плоской волны на границу раздела 2-х сред, плоскость равной фазы волны и плоскость равной амплитуды во второй среде не совпадают (считать n₂₁=n₂/n₁),
• когда угол падения θ>arcsin n₂₁.

№ 83
Полное внутреннее отражение волны от границы раздела двух сред наблюдается,
• когда θ_пад>arcsin n₂₁.

№ 84
Волны распространяются в диэлектрических волноводах (ε_q),
• если θ>arcsin(|n_q/n₀|).

№ 85
Зависимость коэффициента отражения вертикально-поляризованной волны от угла падения на границу раздела двух сред, имеющих волновые сопротивления W₁ и W₂.

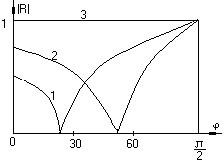
Электрофизические параметры или волновые сопротивления для кривых 1,2,3:
• W₂(3)>W₂(2)>W₂(1); W₁ - воздух.

№ 86
Волна произвольной поляризации падает на границу раздела двух сред. Коэффициент преломления равен 0, а коэффициент отражения равен 1 и -1:
• если среда - идеальный металл, R_в=1, R_г=-1.

№ 87
Чтобы плоская волна не отражалась от второй среды, необходимо:
• чтобы волна падала под углом Брюстера.

№ 88
На плоский медный лист достаточно больших размеров нормально падает плоская волна с длиной 0,1 м. Амплитуда напряженности электрического поля волны составляет E_m=10³ B/м. Мощность, теряемая на нагрев 1 см² поверхности листа в средней его части, если удельная проводимость меди 6*10⁷ 1/ом*м:
• 3,57*10³ Bm.

№ 89
В теории волноводов, из уравнений

где χ - поперечное волновое число; β - постоянная распространения.
• можно определить поперечные компоненты и через продольные.

№ 90
Волновод прямоугольного сечения (a × b). Если рабочую частоту оставлять неизменной, а волновод полностью заполнять диэлектриком с относительной диэлектрической проницаемостью ε_r2>ε_r1>1:
• длина волны λ_B с ростом ε_r уменьшается.

№ 91
По формуле:

в волноводе следует определять связь между поперечными компонентами полей:
• для Е-волн.

№ 92
Фазовая постоянная распространения волны H₀₂ в прямоугольном волноводе, заполненном диэлектриком на длине волны λ₀ (размеры волновода (a × b)) будет иметь вид:
• .

№ 93
Чтобы установить (убедиться) что в прямоугольном волноводе (a × b) на частоте f распространяется волна типа H₂₀, необходимо:
• оценить выполнение неравенства f>f_{кр H20}.

№ 94
Структура поля в поперечном и продольном сечениях прямоугольного волновода

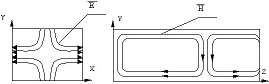
• представлена для типа волны H₁₁.

№ 95
Картина токов в стенках прямоугольного волновода
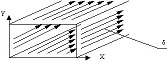t-const.
Она справедлива для типа волны:
• E₁₁.

№ 96
Размеры прямоугольного волновода a × b для работы в диапазоне частот от 3,2 ГГц до 4,0 ГГц на основном типе волны (b=0.5a):
• 72 × 36 мм².

№ 97
Из уравнения κ²-β²-χ²=0 в теории волноводов можно определить:
• постоянную распространения волны в волноводе.

№ 98
Типы волн, наиболее широко использующиеся для передачи энергии в волноводах:
• в круглом - H₁₁, в прямоугольном - H₁₀, в коаксиальном - T.

№ 99
Основной признак волн TE или H в волноводах:
• H_z ≠ 0, E_z=0.

№ 100
Из выражения
, k - волновое число свободного пространства:
• можно определить поперечные электрические компоненты через поперечные магнитные для линий с волнами типа Т.

№ 101
В волноводах могут распространятся:
• длины волн λ₀<λ_кр; частоты f>f_кр.

№ 102
Набор граничных условий для случая прямоугольного волновода:

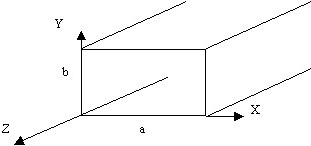
• #ris31.bmp.

№ 103
Мощность, переносимая по прямоугольному волноводу (вдоль оси Z) в случае волны типа H₁₀:
• H_x | _x=0,a=0; H_y | _y=0,b=0.

№ 104
В волноводе a × b=10 × 5 см² напряженность электрического поля в максимуме волны основного типа равна E_m=10³ В/м. Амплитуда поперечного и продольного магнитного поля, а также передаваемая мощность при λ=15 см:
• H_xm=1,75 A/м ; H_zm=1,99 A/м;
• P=2,194 Вт.

№ 105
Уравнение Гельмгольца для магнитных полей в областях, содержащих источники с токами _cm и зарядами ρ̇_cm, для сред с параметрами ε_a и μ_a:
• .

№ 1
Радиоволны частотой 15 МГц:
• Короткие волны.

№ 2
Передающая антенна излучает сигнал мощностью 100 Вт и находится на расстоянии 10 км от приемной. Коэффициент направленного действия обеих антенн 1000, длина радиоволны 40 см. (Считать π² ≈ 10). Мощность сигнала в приемной антенне при распространении радиоволн в свободном пространстве:
• 0,1 мВт.

№ 3
Фазы волн, пришедших в точку приема из первой и пятой зон Френеля, различаются на величину:
• 4π.

№ 4
Радиус первой зоны Френеля для середины трассы протяженностью 40 км при длине волны передатчика 1 м:
• 10 м.

№ 5
Расстояние прямой видимости при одних и тех же высотах поднятия антенн больше:
• на Земле, чем на Луне.

№ 6
Интерференционная формула применима для расчета радиотрасс, когда приемная и передающая антенны:
• подняты над земной поверхностью.

№ 7
Сферичность земли при расчете радиотрасс с использованием интерференционной формулы Введенского, учитывается:
• с помощью приведенных высот.

№ 8
Интерференционная формула Введенского:
• .

№ 9
Можно считать поверхность Земли плоской, если высота неровностей 2 м, угол падения радиоволны на земную поверхность 60°, для диапазонов радиоволн:
• СДВ, ДВ, СВ.

№ 10
Суть “идеализации” в формуле идеальной радиопередачи:
• Не принимается во внимание кривизна земной поверхности, ей приписываются свойства идеального проводника.

№ 11
Поле в дальней зоне, излучаемое вертикальным вибратором, расположенным на полупроводящей Земной поверхности, имеет:
• вертикальную и горизонтальную составляющие.

№ 12
Амплитуда напряженности электрического поля, создаваемая вертикальным вибратором, расположенным вблизи идеально проводящей, плоской поверхности больше амплитуды напряженности электрического поля, создаваемой вибратором той же мощности в свободном пространстве:
• в √2 раз.

№ 13
Численное расстояние в формуле Шулейкина - Ван-дер-Поля:
• ρ=πr/(λ*|ε|).

№ 14
Расстояние прямой видимости за счет тропосферной рефракции при градиенте коэффициента преломления тропосферы dn/dh=-R₀/2:
• увеличится в √2 раз.

№ 15
Радиус кривизны траектории луча в тропосфере при изменении градиента показателя преломления от dn/dh=-3*10⁸м^-1 до dn/dh=-6*10⁸м^-1:
• Уменьшится в 2 раза.

№ 16
Эквивалентный радиус Земли для тропосферы с градиентом показателя преломления dn/dh=-4*10⁸м^-1:
• 3R₀/4 раз.

№ 17

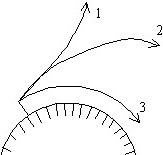
критической тропосферной рефракции соответствует:
• третий луч.

№ 18
Замирания сигналов в линиях радиосвязи с тропосферным рассеянием вызваны:
• Флуктуациями неоднородностей тропосферы.

№ 19
Волновой процесс в среде, где ε<0:
• возможен, но при условии, что и магнитная проницаемость (?) тоже отрицательная.

№ 20
Собственная частота ионизации электронного газа, если концентрация электронов в нем увеличится в 4 раза:
• увеличится в 2 раза.

№ 21
Высота точки отражения в ионосфере при уменьшении частоты радиоволны:
• уменьшится.

№ 22
Максимальная электронная концентрация N_max=5*10⁶ эл/см³. Критическая частота для вертикально падающей на ионосферу волны.:
• 20 МГц.

№ 23
- падающей на ионосферу под углом 60°:
• 40 МГц.